• Home
• Project
  • Overview
  • Control
    • Target
    • Inhibitor
  • Cleanse
    • Antibiofilm
    • Attachment
  • Care
  • L. casei
  • HOPErfusion
• Modeling
  • Overview
  • Growth&pH
  • Competition
  • Threshold
  • Stephen curve
  • Effectiveness
  • new part 1
  • new part 2
• Safety
• Notebook
  • Lab notes
  • Protocol
• Human Practice
• Team
  • Members
  • Gallery
  • NYMU
  • Cooperation

Growth curve & pH model

Purpose

Introduction: Growth Curve

A growth curve for a population of bacteria illustrates some of the dynamics that affect the population size over time.
Four distinct phases are recognized:

The lag phase:
The curve remains at a plateau. During this time, bacteria adapt to their new environment, store nutrients and prepare for binary fission.

The logarithmic phase:
This phase is also called the exponential growth phase: the population of bacteria enters an active stage of growth, the mass of each cell increases rapidly, and the number of bacteria doubles.

The stationary phase:
At this stage reproductive and death rates equalize, the population enters another plateau.

Models and mathematic equations

Three well known growth models (Logistic, Gompertz, and Richartz)are used in this work. Characteristic model parameters (such as lag phase (λ), maximal growth rate (µ-max slope), stationary phase (A-max growth value)) are derived from our experimental data. Bootstrap and cross-validation techniques are used for estimating confidence intervals of all derived parameters.

The aim is to integrate the experimental data into different growth models and to compare the models using statistical methods (AIC and maximum likelihood were used). We believe, and many scientists do, that model selection is the most important part in model-experiment based research-The right data with the right model.

Logistic Model: $$\begin{align} y(t)&=\frac{A}{1+\exp\left(\frac{4\mu}{A}(\lambda-t)+2\right)} \end{align}$$ Gompertz Model: $$\begin{align} y(t)&=A.\exp\left[-\exp\left(\frac{\mu.\exp(1)}{A}(\lambda-t)+1\right)\right] \end{align}$$ Richartz Model: \begin{align} y(t)&=A.\left[1+\nu\exp\left(1+\nu+\frac{\mu}{A}(1+\nu)^{1+1/\nu}(\lambda-t)\right)\right]^{-1/\nu} \end{align} $\nu$ is a shape parameter (in the richartz model only)

pH model

Existed model is \begin{align} \frac{dpH}{dP}&=k(pH-pH_{min}) %pH&=pH_{min}+\left(pH_{0}-pH_{min}\right)^{-k(P-P_{0})} \end{align} However, this model is not appropriate for our experimental data; we used linear regression model instead. \begin{align} \label{eq:reg} pH=\alpha + \beta OD +\epsilon \end{align} where $\epsilon$ is a random error or noice (which helps to capture a measurement error and other unknown factors). And it is assumed to be Gaussian (normal distribution function), $\epsilon = N(\theta,\sigma^{2})$, with mean $\theta$ and constant variance $\sigma^{2}$. $\alpha$ and $\beta$ are model parameters.

Result and model validation

Figure 1: Simulation results of the growth curve

Our experimental data are implemented in the three proposed models. AIC is used to measure the performance of the models and the result shows that Logistic and Richartz models are approximately the same, but slightly different from Gompertz. However, using 95% confidence interval all of them are appropriate to fit the given data.

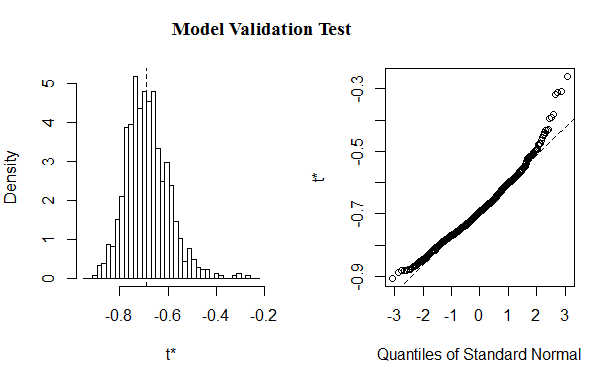
Figure 2: Shows validation test(t*) for the fitted model

The validation test (plot of the residuals), as Figure 2, shows that the simulation result obtained from bootstrap samples is suitable to estimate the model parameters.

Using our experimental data as initials samples, we applied Bootsrap statistical to sample empirical data. The simulated result is presented as Figure (1). And, the estimated model parameters (mu(µ), lamda(λ), A) are summarized as Table 1. $$\text{Table 1: Estimated Model Parameter}$$

-------------------------------------------
           mu          lamda         A    
===========================================
Lower     0.294        16.041       1.155  
Mean      0.384        16.456       1.187  
Upper     0.474        16.871       1.220  
Std       0.046        0.212        0.016  
------------------------------------------- 
Integral value: 16.622   
------------------------------------------- 

From the result on table $1$, the $lower$ and $upper$ values are the estimated confidence intervals of the corresponding parameters. $Std$-standard deviation) and $mean$-average values are obtained from the bootstrap samples. These results are used in the proposed three growth models. After the approprate models are selected (in our case, the three proposed models are equally approprate), the parameters are taken as an intial values for the interaction model; which is used to study the growth of S.mutant in the presence of other species(see competition model).

Reference