Introduction
This part aims to simulate the circuit of the Target part, which will be turn on when S. mutans is too much or phage is unable to control the S. mutans quorum.
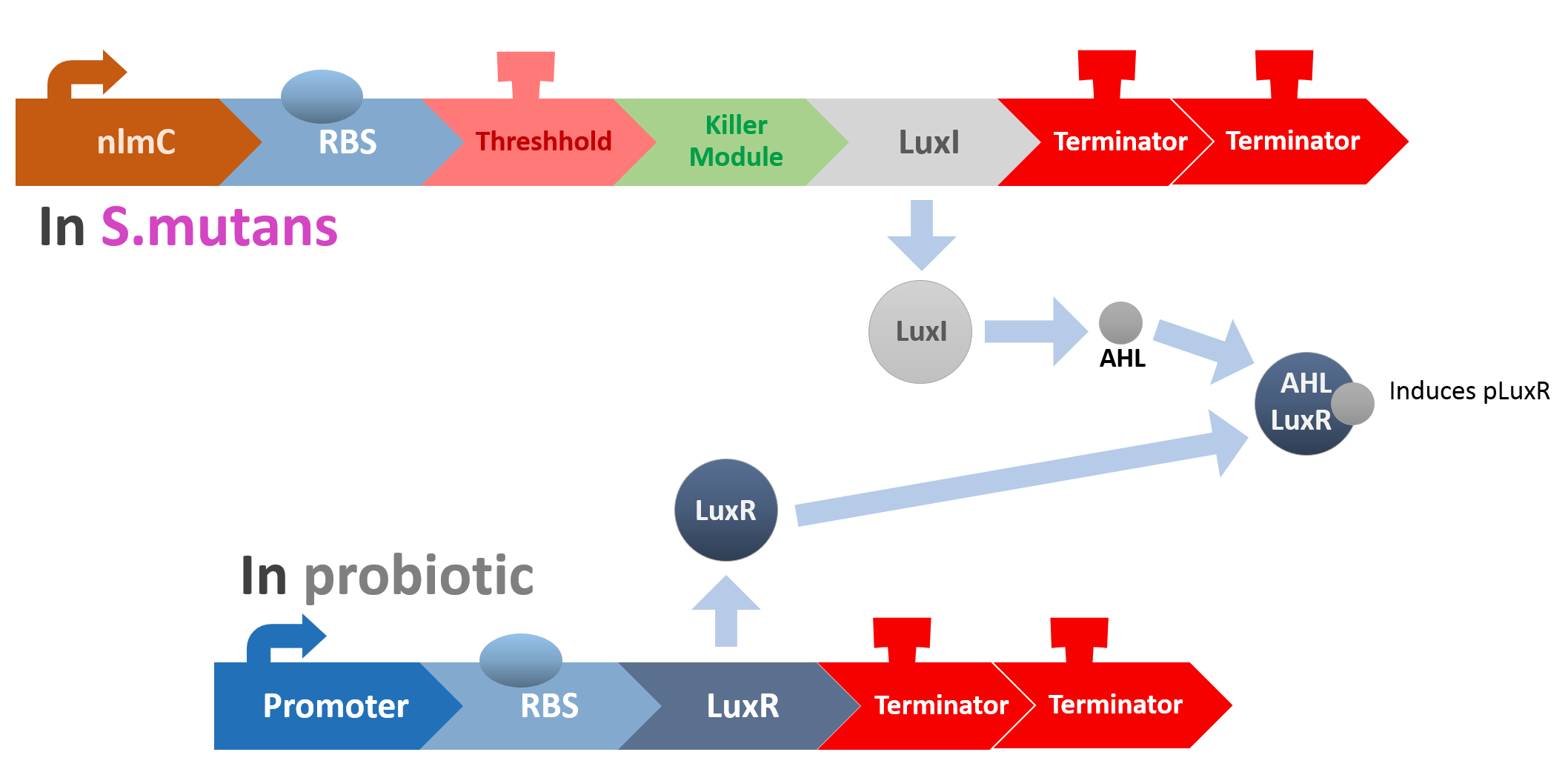
LuxI coding sequence is controlled by nlmC promoter and threshold terminator. When the quorum of S. mutans is too much, the LuxI will be expressed and generate AHL-synthase. LuxR, on the other hand, is generated by E. coli constitutively. The LuxR and AHL can form a complex that can activate the pLuxR promoter. In our design, pLuxR promoter in E. coli can activate the lysine protein that can kill S. mutans only.
We model this part to see how the circuit works if phage is unable to control the S. mutans quorum, so the initial state of comE, the molecule that triggers the nlmC promoter, has a certain amount, which means the S. mutans is out of control.
System
(1)
Circuit triggered by nlmC promoter. When S. mutans quorum is out of control, the amount of comE will increase and offset the effect of threshold terminator. luxI will be expressed.
$$\frac{d[\text{luxI mRNA}]}{dt}=P_{nlmC} \frac{[\text{comE}]^{n1}}{K_{d1}+[\text{comE}]^{n1}} (1-a)^x - K_{deg\_mluxI} [\text{luxI mRNA}]$$
$$\frac{d[\text{luxI}]}{dt}= K_{t1} [\text{luxI mRNA}] - K_{deg\_luxI} [\text{luxI}]$$
1. $P_{nlmC}$:max nlmC promoter activity
2. $K_{d1}$:promoter-TF dissociation constant
3. $K_{deg\_mluxI}$:luxI mRNA degradation
4. $(1-a)^x$:terminator effect
5. $K_{t1}$:Translation efficiency
6. $K_{deg\_luxI}$:luxI degredation
7. $n_1$:hill coefficient
(2)
luxR is expressed by a constitutive promoter. However, without luxI, it doesn't have any function in this system.
$$\frac{d[\text{luxR mRNA}]}{dt}=P_{const} - K_{deg\_mluxR} [\text{luxR mRNA}]$$
$$\frac{d[\text{luxR}]}{dt}= K_{t2} [\text{luxR mRNA}] - K_{deg\_luxR} [\text{luxR}]-K_{on}[\text{AHL}]^2[\text{luxR}]+K_{off}[\text{AHLluxR}]$$
1. $P_{const}$:constitutive promoter activity
2. $K_{deg\_mluxR}$:luxR mRNA degradation
3. $K_{t2}$:Translation efficiency
4. $K_{deg\_luxR}$:luxR degredation
5. $K_{on}$: reaction rate of $\text{2AHL+luxR} \rightarrow \text{AHLluxR(complex)}$
6. $K_{off}$: reaction rate of $\text{AHLluxR(complex)} \rightarrow \text{2AHL+luxR}$
(3)
AHL, N-Acyl homoserine lactones. The product of LuxI catalyses the synthesis of AHL. AHL and luxR can form a complex.
$$\frac{d[\text{AHL}]}{dt}= K_{AHL} [\text{luxI}] +2 K_{off}[\text{AHLluxR}] -2 K_{on}[\text{AHL}]^2[\text{luxR}] - K_{deg\_AHL}$$
1. $K_{AHL}$:synthesis rate of AHL by LuxI
(4)
Complex of AHL and luxR. The complex can activate pluxR promoter.
$$\frac{d[\text{AHLluxR}]}{dt}= K_{on}[\text{AHL}]^2[\text{luxR}] - K_{off}[\text{AHLluxR}]$$
1. reaction of $\text{2AHL+luxR} \rightarrow \text{AHLluxR(complex)}$
(5)
Circuit triggered by pluxR promoter. The lysine protein can kill S. mutans. The lysine protein is original from phage M102.
$$\frac{d[\text{lysine gene mRNA}]}{dt}=P_{luxR} \frac{[\text{AHLluxR}]^{n2}}{K_{d2}+[\text{AHLluxR}]^{n2}} - K_{deg\_mlys} [\text{lysine gene mRNA}]$$
$$\frac{d[\text{lysine protein}]}{dt}= K_{t2} [\text{lysine gene mRNA}] - K_{deg\_lys} [\text{lysine protein}]$$
1. $P_{luxR}$:max pluxR promoter activity
2. $K_{d2}$:promoter-TF dissociation constant
3. $K_{deg\_mlyx}$:lysine gene mRNA degradation
4. $K_{t2}$:Translation efficiency
5. $K_{deg\_lys}$:lysine protein degredation
6. $n_2$:hill coefficient
Result
The result shows that once the concentration of comE offset the threshold terminator, it would trigger the downstream circuits and finally generate lysine protein to help phage kill S. mutans.

The result indicates that there is lag phase before lysine protein accumulating to a higher amount. The lag phase is approximately 30 minutes. In our Stephen curve model, it only takes about 10 minutes for the pH to drop to its minimum level. This model is not for short time S. mutans eliminating, it is for normal prevention in case that phage might not be able to control S. mutans for certain reasons.
Reference
- 2011 igem team: ETH_Zurich
- 2013 igem team: NYMU_Taipei
- Weber and Buceta BMC Systems Biology 2013 7:6
 "
"