Latest revision as of 01:18, 18 October 2014

Modeling

Overview

An important part of our project is devoted to the concrete realization of a lemon by moulding it from agar gel. It is well explained in the lemon shaping part.

But, before starting more investigations and more experimentation, there is a real need to ensure that our project is feasible. We will tackle these following points :

By cutting a lemon, there is a slight yellow/green color on the surface and white on the inside. To reproduce this effect, we use a kill-switch system based on oxygen and had been achieved by the team iGEM Paris Saclay 2013. The more we penetrate into the gel, the less oxygen is present, the less kill-switch system is activated, the less bacteria will produce desired color, and the whiter the interior. For this, we must ensure that oxygen does not penetrate completely into the lemon. We decided to model oxygen diffusion into the gel.

A major issue is the development of our bacteria in an agar medium. We noticed that the bacteria inside the gel grew less than those on the outside. We model the bacterial growth

To be even closer to the reality, we will imitate the ripening process of a real lemon. We wanted to test if we could get a green color by fusion of two chromoproteins one yellow and one blue.

Lastly, we obtain the lemon scent by modifying E.coli in order to let it produce pinene, limonene and geraniol but this does not ensure us that we will smell the lemon fragrance.

For all these reasons, modeling is really important for the concrete realization of our artwork and in general in an iGEM project!

Oxygen Diffusion

Is it possible to have a crust on the surface of the lemon by producing a "lemon coloration-like" by our bacteria ?

We invite you to discover how we modelled the oxygen diffusion in order to answer this question.

Now that we know if bacteria could develop in agar or not, a natural issue is to predict the bacterial growth. So, this part aims at predicting over time the bacterial population growth on an ellipsoidal object - a fake lemon in practice -. More precisely, we have to determine the threshold of the initial proportion of bacteria for which we are sure that the population will never extinct... if this threshold exists!

Fusion Protein

Paris Saclay BlueChromoSwissModStruct.png

An important aspect of our project is the color transition from green to yellow, in order to emulate the lemon maturation. To do this, we use a fusion protein. Before starting the fusion of the two chromoproteins -yellow and blue-, we have checked for their respective compatibility. That's why we discuss the structural modeling of the proteins.

Lemon Scent

We need criteria to assess the scent of lemon. For this, we have process as follow:

We evaluate the evolution of the concentrations of three fragrances over time.
We give a procedure for estimating a suitable time interval in which we can say that we got the lemon smell as desired.

Note : Do not be afraid and run away because of seing mathematical formulae : Maths is fun and we have made a real effort to be as precise as possible in order non-mathematicians to understand. For example, in order not to disgust poor mathematical readers of others, we will just add one or two -for the warrior- star(s) to parts which need more mathematical background. Morever, we illustrated our work with figures which could be understood for themselves, without knowing the method to get them.

@@ Line 1: / Line 1: @@
-{{Team:Paris_Saclay/default_header}}
+{{Team:Paris_Saclay/modeling_header}}
 =Modeling=
-To realise our artwork, we use an agarose gel to obtain the shape of a lemon. To push the resemblance to the extreme, we wish to have a crust in the edge of the lemon when we seperate it. In fact, we build bacteria who produce yellow/green color in presence of oxygen. Thus we must evaluate the penetration of the oxygen in the gel !
+==Overview==
+An important part of our [https://2014.igem.org/Team:Paris_Saclay/Project project] is devoted to the concrete realization of a lemon by moulding it from agar gel. It is well explained in the [https://2014.igem.org/Team:Paris_Saclay/Project/Lemon_Shaping lemon shaping] part.
-Oxygen penetrates into the gel by diffusion phenomenon that we will study below. We first use the following phenomenological law suggest by Adolphe Fick in 1855:
+But, before starting more investigations and more experimentation, there is a real need to ensure that our project is feasible. We will tackle these following points :
+*By cutting a lemon, there is a slight  yellow/green color on the surface and white on the inside. To reproduce this effect, we use a kill-switch system based on oxygen and had been achieved by the team iGEM Paris Saclay 2013. The more we penetrate into the gel, the less oxygen is present, the less kill-switch system is activated, the less bacteria will produce desired color, and the whiter the interior. For this, we must ensure that oxygen does not penetrate completely into the lemon. We decided to model [https://2014.igem.org/Team:Paris_Saclay/Modeling/oxygen_diffusion oxygen diffusion] into the gel.
-----
+*A major issue is the development of our bacteria in an agar medium. We noticed that the bacteria inside the gel grew less than those on the outside. We model the bacterial growth
-'' In an homogeneous and isotropic environment, containing particles distributed inhomogeneously,appears spontaneously a volumetric flow density vector particle $\overrightarrow{J}(M,t) $. In any point $M$ in space, this vector is proportional to the gradient of the particle density $n(M,t)$. Mathematicaly, this relationship take the form:  \[  \overrightarrow{J}(M,t) = - D  \times \nabla  n(M,t) \qquad (1) \]  where $D$ is the diffusion coefficient and $\nabla$ is the gradient vector.''
+*To be even closer to the reality, we will imitate the [https://2014.igem.org/Team:Paris_Saclay/Project/Salicylate_Inducible_System ripening process] of a real lemon. We wanted to test if we could get a green color by fusion of two chromoproteins one yellow and one blue.
+*Lastly, we obtain the [https://2014.igem.org/Team:Paris_Saclay/Project/Lemon_Scent lemon scent] by modifying ''E.coli'' in order to let it produce ''pinene'', ''limonene'' and ''geraniol'' but this does not ensure us that we will smell the lemon fragrance.
-----
+For all these reasons, modeling is really important for the concrete realization of our artwork and in general in an iGEM project!
-In equation after Fick's law above, we need to know the parameter $D$. We then searched in scientific literature and article '''[1]'''  describes a method to get it. Referring to this article,  the diffusion coefficient of oxygen in agarose is $ D = 0{,}256 \times 10^{-8} m^2 s^{-1} $.
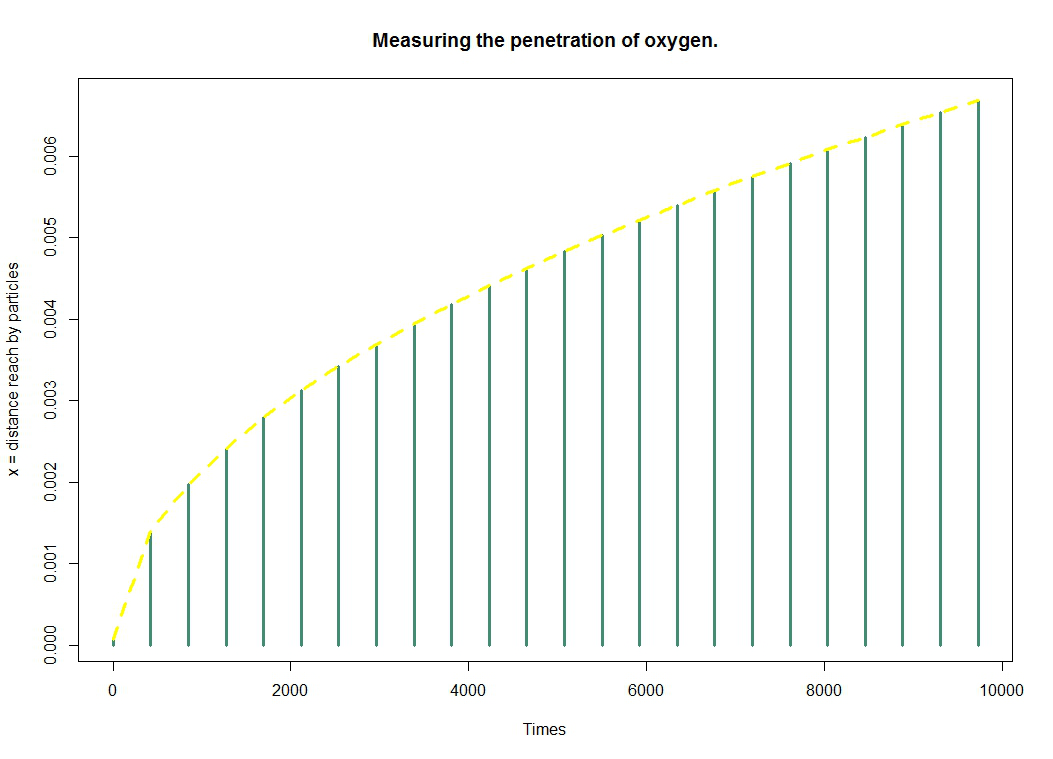
+==[https://2014.igem.org/Team:Paris_Saclay/Modeling/oxygen_diffusion Oxygen Diffusion]==
-The phenomenon we are facing is quite difficult to tackle if taken as a whole and We must emit a number of intuitively acceptable hypothesis.
-* To simplify the problem, we consider that the diffusion of oxygen particle occurs only in one direction. So $\overrightarrow{J}(M,t) = J(x,t) \overrightarrow{e}_x $. This hypothesis is credible because we seek the maximum penetrance of oxygen. This is why we consider that the diffusion occurs in the line of greatest slope.
-* Spatial variations in the density of particles are connected to spatial variations of the vector $\overrightarrow{J}(M,t)$ by '''the material's equation of conservation''' in presence of volume distribution of particle source $\sigma (x,t)$ (device which injects or subtracted particles to the system) :
+[[File:Paris_Saclay_oxygenpenetration.png|left|150px]]
-\[ \frac{\partial n}{\partial t} (x,t) = - \frac{\partial J}{\partial x} (x,t) + \sigma (x,t)  \qquad (2) \]
-By replacing $(2)$ in $(1)$, we obtain the following '''equation of diffusion''' :
+''Is it possible to have a crust on the surface of the lemon by producing a "lemon coloration-like" by our bacteria ?''
-\[ \forall t, \forall x,  \bigg(  \frac{\partial}{\partial t} - D \frac{\partial^2}{\partial x^2} \bigg) n(x,t) =  \sigma (x,t)  \qquad (3) .\]
-As our lemon is exposed to the ambient air, we stay in steady state where the source $ \sigma (x,t) $ is equal to $N_0$ the quantity of $O_2$  in the air.
+We invite you to discover how we modelled the [https://2014.igem.org/Team:Paris_Saclay/Modeling/oxygen_diffusion oxygen diffusion] in order to answer this question.
-To solve this equation, we use Fourier's analysis and it is kwown (classical solution of the heat equation) that
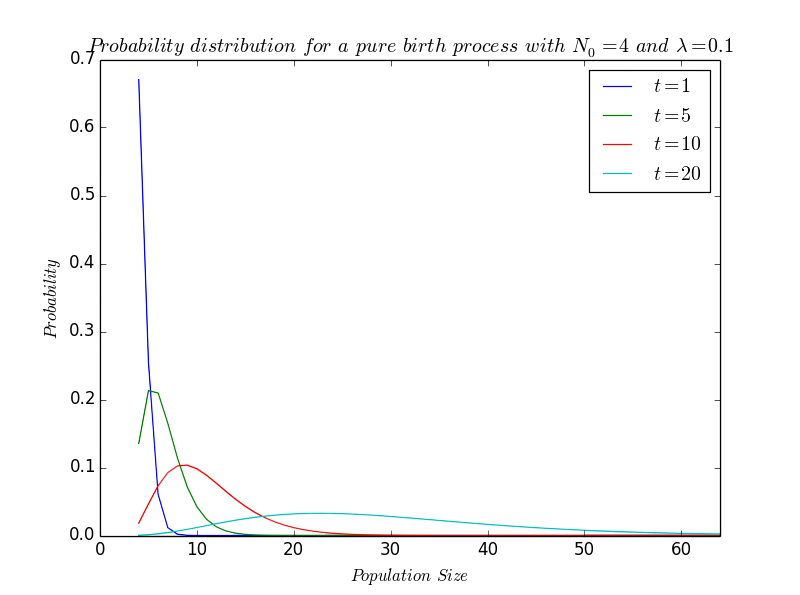
+==[https://2014.igem.org/Team:Paris_Saclay/Modeling/bacterial_Growth Bacterial Growth]==
-\[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg)  + \int_{0}^{t} \underbrace{N_0 * exp \bigg(- \frac{|x|^2}{4 D \tau} \bigg)}_{= 0 \text{ by symmetry of the gaussian distribution }} \frac{d\tau}{\sqrt{4 \pi D \tau} }  \]
+[[File:Paris_Saclay_Pure_Birth_Process.png|left|150px]]
-Whence, \[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) \]
+Now that we know if bacteria could develop in agar or not, a natural issue is to predict the [https://2014.igem.org/Team:Paris_Saclay/Modeling/bacterial_Growth bacterial growth].
+So, this part aims at predicting over time the bacterial population growth on an ellipsoidal object - a fake lemon in practice -.
+More precisely, we have to determine the threshold of the initial proportion of bacteria for which we are sure that the population will never extinct... ''if this threshold exists!''
-Thus we deduce easily that the average dispersion particle is given by the variance $\Delta x = \sqrt{2Dt}$. Using this formula, we deduct that, for example, oxygen will penetrate $3 \times 10^{-3} m$ in $1956.522 s = 32.6082 $ minutes.
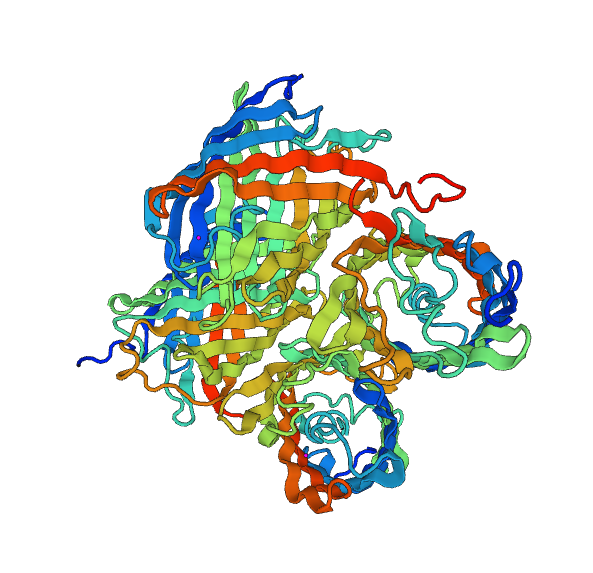
+==[https://2014.igem.org/Team:Paris_Saclay/Modeling/Fusion_Proteine Fusion Protein]==
-The charts below give us a very clear idea of penetrance evaluated over time.
+[[File:Paris_Saclay_BlueChromoSwissModStruct.png|left|150px]]
-=== Graphical visualization ===
+An important aspect of our project is the color transition from green to yellow, in order to emulate the lemon maturation.
+To do this, we use a [https://2014.igem.org/Team:Paris_Saclay/Modeling/Fusion_Proteine fusion protein]. Before starting the fusion of the two chromoproteins -yellow and blue-, we have checked for their respective compatibility. That's why we discuss the structural modeling of the proteins.
-[[File:Paris_Saclay_oxygenGraph.jpeg|600px]]
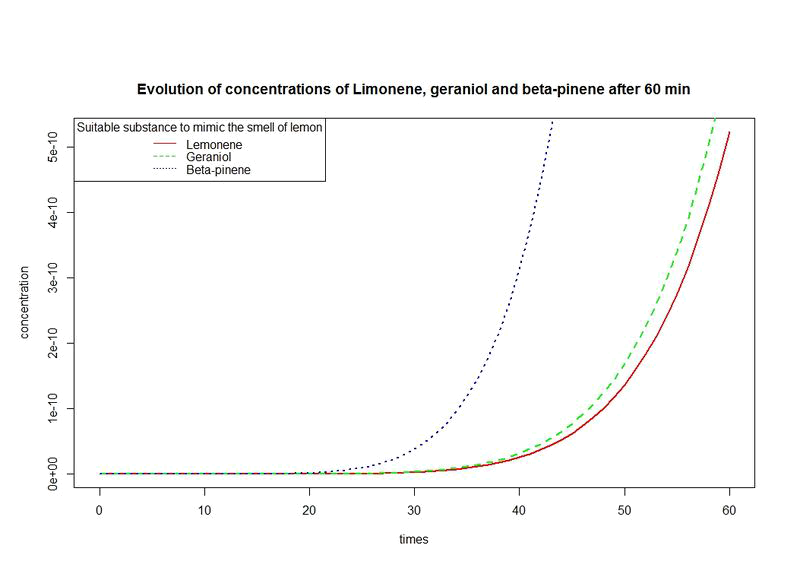
+==[https://2014.igem.org/Team:Paris_Saclay/Modeling/odor Lemon Scent]==
+[[File:Paris_Saclay_odor_60.png|left|150px]]
+We need criteria to assess the scent of lemon. For this, we have process as follow:
+* We evaluate the evolution of the concentrations of three fragrances over time.
+* We give a procedure for estimating a suitable time interval in which we can say that we got the lemon smell as desired.
-[[References:]]
+----
-'''[1]''' A.C. Hulst, H.J.H. Hens, R.M. Buitelaar and J. Tramper, ''Determination of the effective diffusion coefficient of oxygen in gel materials in relation to gel concentration'', Biotechnology Techniques Vol 3 No 3 199-204 (1989).
-'''[2]''' Vincent Renvoizé, ''Physique PC-PC*'', Cap Prepas, Pearson Education, 2010.
+'''Note''' : Do not be afraid and run away because of seing mathematical formulae : ''Maths is fun'' and we have made a real effort to be as precise as possible in order non-mathematicians to understand. For example, in order not to disgust poor mathematical readers of others, we will just add one or two -for the warrior- star(s) to parts which need more mathematical background. Morever, we illustrated our work with figures which could be understood for themselves, without knowing the method to get them.
 {{Team:Paris_Saclay/default_footer}}

Team:Paris Saclay/Modeling

From 2014.igem.org