Team:Paris Saclay/Modeling/oxygen diffusion
From 2014.igem.org
(→Modeling) |
(→Oxygen Diffusion) |
||
| (25 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Team:Paris_Saclay/modeling_header}} | {{Team:Paris_Saclay/modeling_header}} | ||
| - | = | + | = Oxygen Diffusion = |
| - | + | ||
| - | + | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | To realise our artwork, we use an agar gel to obtain the shape of a lemon. To push the resemblance to the extreme, we wish to have a crust in the edge of the lemon when we separate it. We note that ''E.coli'' can live in an anaerobic environment. Thus, with this property combined with the ease of access to oxygen, we solve the problem by making our ''E.coli'' react only in contact with oxygen. In fact, we build bacteria who produce yellow/green color in presence of oxygen. Since we just want a crust, it is not necessary that all our bacteria react. Hence the necessity to estimate the penetration of oxygen into the gel. | |
| - | + | == Building the model == | |
| - | Oxygen penetrates into the gel by diffusion phenomenon that we will study below. We first use the following phenomenological law | + | Oxygen penetrates into the gel by diffusion phenomenon that we will study below. We first use the following phenomenological law suggested by Adolphe Fick in 1855: |
---- | ---- | ||
| - | '' In an homogeneous and isotropic environment, containing particles distributed inhomogeneously,appears spontaneously a volumetric flow density vector particle $\overrightarrow{J}(M,t) $. In any point $M$ in space, this vector is proportional to the gradient of the particle density $n(M,t)$. | + | '' In an homogeneous and isotropic environment, containing particles distributed inhomogeneously, appears spontaneously a volumetric flow density vector particle $\overrightarrow{J}(M,t) $. In any point $M$ in space, this vector is proportional to the gradient of the particle density $n(M,t)$. Mathematically, this relationship takes the form: \[ \overrightarrow{J}(M,t) = - D \times \nabla n(M,t) \qquad (1) \] where $D$ is the diffusion coefficient and $\nabla$ is the gradient vector.'' |
---- | ---- | ||
| - | In equation | + | In equation from Fick's law above, we need to know the parameter $D$. We then searched in scientific literature and the article '''[1]''' describes a method to get it. Referring to this article, the diffusion coefficient of oxygen in agarose is $ D = 0{,}256 \times 10^{-8} m^2 s^{-1} $. |
| - | The phenomenon we are facing is quite difficult to tackle if taken as a whole and | + | The phenomenon we are facing is quite difficult to tackle if taken as a whole and we must emit a number of intuitively acceptable hypotheses: |
* To simplify the problem, we consider that the diffusion of oxygen particle occurs only in one direction. So $\overrightarrow{J}(M,t) = J(x,t) \overrightarrow{e}_x $. This hypothesis is credible because we seek the maximum penetrance of oxygen. This is why we consider that the diffusion occurs in the line of greatest slope. | * To simplify the problem, we consider that the diffusion of oxygen particle occurs only in one direction. So $\overrightarrow{J}(M,t) = J(x,t) \overrightarrow{e}_x $. This hypothesis is credible because we seek the maximum penetrance of oxygen. This is why we consider that the diffusion occurs in the line of greatest slope. | ||
| - | * Spatial variations in the density of particles are connected to spatial variations of the vector $\overrightarrow{J}(M,t)$ by '''the material's equation of conservation''' in presence of volume distribution of particle source $\sigma (x,t)$ (device which injects or | + | * Spatial variations in the density of particles are connected to spatial variations of the vector $\overrightarrow{J}(M,t)$ by '''the material's equation of conservation''' in presence of volume distribution of particle source $\sigma (x,t)$ (device which injects or subtracts the particles to the system) : |
\[ \frac{\partial n}{\partial t} (x,t) = - \frac{\partial J}{\partial x} (x,t) + \sigma (x,t) \qquad (2) \] | \[ \frac{\partial n}{\partial t} (x,t) = - \frac{\partial J}{\partial x} (x,t) + \sigma (x,t) \qquad (2) \] | ||
By replacing $(2)$ in $(1)$, we obtain the following '''equation of diffusion''' : | By replacing $(2)$ in $(1)$, we obtain the following '''equation of diffusion''' : | ||
| - | \[ \forall t, \forall x, \bigg( \frac{\partial}{\partial t} - D \frac{\partial^2}{\partial x^2} \bigg) n(x,t) = \sigma (x,t) | + | \[ \boxed{ \forall t>0, \forall x, \bigg( \frac{\partial}{\partial t} - D \frac{\partial^2}{\partial x^2} \bigg) n(x,t) = \sigma (x,t) } \qquad (3) \] |
| - | As our lemon is exposed to the ambient air, we stay in steady state where the source $ \sigma (x, | + | As our lemon is exposed to the ambient air, we stay in steady state where the initial source $ \sigma (x,t_0) $ is equal to $N_0$ the quantity of $O_2$ in the air and $ \sigma (x,t) = 0 $ pour tout $ t > t_0$. |
| - | To solve this equation, we use Fourier's analysis and | + | To solve this equation, we use Fourier's analysis and the solution is well known: we have the same expression as the '''''"heat equation"''''' |
| - | \[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) | + | \[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) \] |
| - | |||
| - | Thus we deduce easily that the average dispersion | + | Thus we deduce easily that the average dispersion of the particles is given by the variance $\boxed{ \Delta x = \sqrt{2Dt} }$. Using this formula, we deduct that, for example, oxygen will penetrate $3 \times 10^{-3} m$ in $1956.522 s = 32.6082 $ minutes. |
| + | |||
| + | We recommend reading the reference '''[2]'''. Content is accessible from the first year of university. | ||
The charts below give us a very clear idea of penetrance evaluated over time. | The charts below give us a very clear idea of penetrance evaluated over time. | ||
| Line 49: | Line 44: | ||
=== Graphical visualization === | === Graphical visualization === | ||
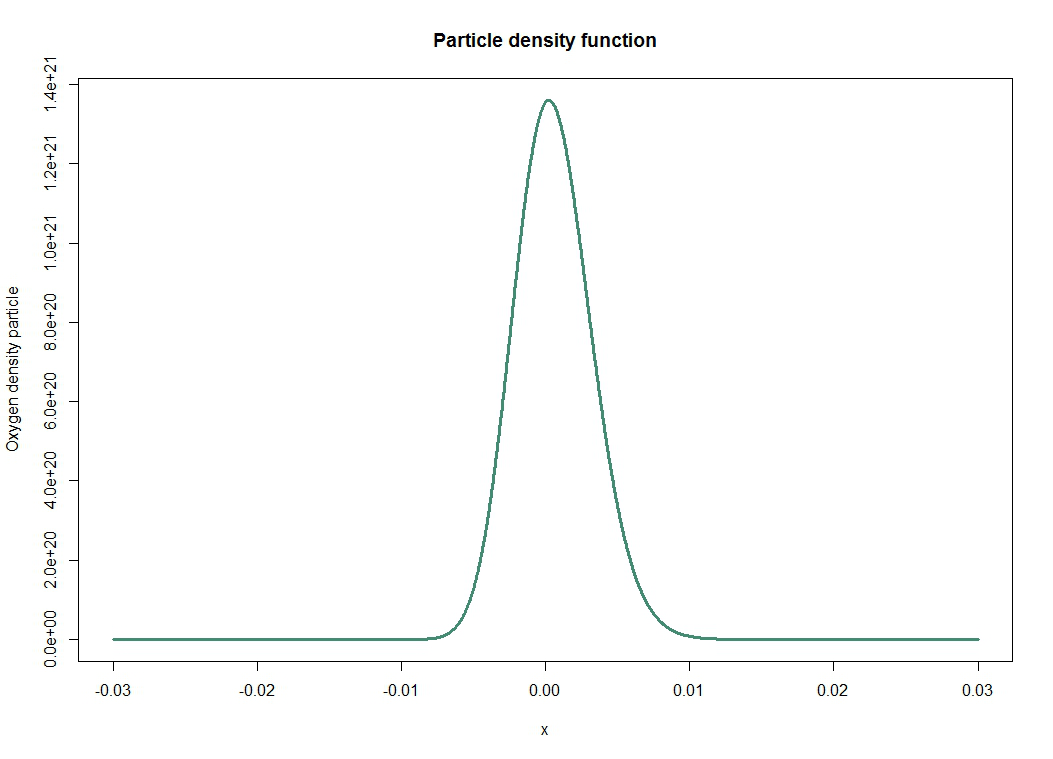
| - | [ | + | We represent in the first figure the solution of the diffusion equation that was previously established. This basically tells us the mean and the average dispersion of particles: it is a probability density given by |
| + | |||
| + | \[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) \] | ||
| + | |||
| - | + | [[File:Paris_Saclay_oxygendensity.png|700px|center]] | |
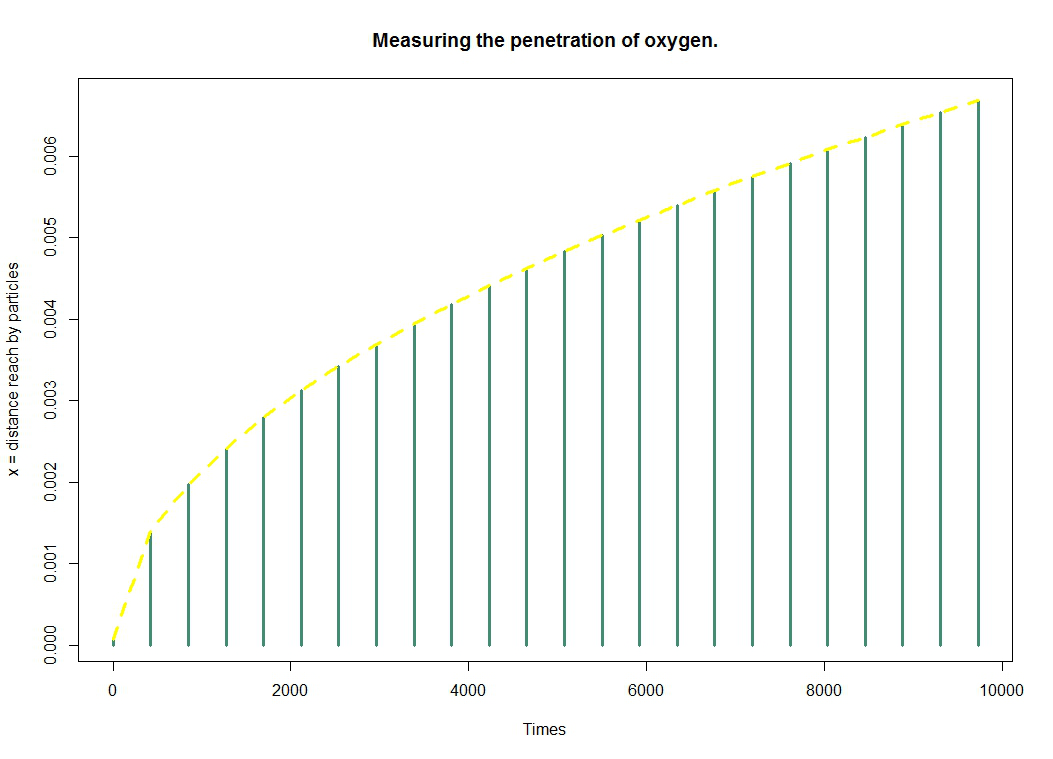
| + | Remember that the purpose of this model is to provide information on the penetration of oxygen into the gel. The figure represents the distance reached by oxygen particles over time. We get it through the formula $ \Delta x = \sqrt{2Dt} $. | ||
| - | + | [[File:Paris_Saclay_oxygenpenetration.png|700px|center]] | |
| - | + | It is now important to study how our bacteria will develop in the agar gel. This is well done in this [https://2014.igem.org/Team:Paris_Saclay/Modeling/bacterial_Growth page]. | |
| - | + | == References == | |
'''[1]''' A.C. Hulst, H.J.H. Hens, R.M. Buitelaar and J. Tramper, ''Determination of the effective diffusion coefficient of oxygen in gel materials in relation to gel concentration'', Biotechnology Techniques Vol 3 No 3 199-204 (1989). | '''[1]''' A.C. Hulst, H.J.H. Hens, R.M. Buitelaar and J. Tramper, ''Determination of the effective diffusion coefficient of oxygen in gel materials in relation to gel concentration'', Biotechnology Techniques Vol 3 No 3 199-204 (1989). | ||
Latest revision as of 01:11, 18 October 2014

Contents |
Oxygen Diffusion
To realise our artwork, we use an agar gel to obtain the shape of a lemon. To push the resemblance to the extreme, we wish to have a crust in the edge of the lemon when we separate it. We note that E.coli can live in an anaerobic environment. Thus, with this property combined with the ease of access to oxygen, we solve the problem by making our E.coli react only in contact with oxygen. In fact, we build bacteria who produce yellow/green color in presence of oxygen. Since we just want a crust, it is not necessary that all our bacteria react. Hence the necessity to estimate the penetration of oxygen into the gel.
Building the model
Oxygen penetrates into the gel by diffusion phenomenon that we will study below. We first use the following phenomenological law suggested by Adolphe Fick in 1855:
In an homogeneous and isotropic environment, containing particles distributed inhomogeneously, appears spontaneously a volumetric flow density vector particle $\overrightarrow{J}(M,t) $. In any point $M$ in space, this vector is proportional to the gradient of the particle density $n(M,t)$. Mathematically, this relationship takes the form: \[ \overrightarrow{J}(M,t) = - D \times \nabla n(M,t) \qquad (1) \] where $D$ is the diffusion coefficient and $\nabla$ is the gradient vector.
In equation from Fick's law above, we need to know the parameter $D$. We then searched in scientific literature and the article [1] describes a method to get it. Referring to this article, the diffusion coefficient of oxygen in agarose is $ D = 0{,}256 \times 10^{-8} m^2 s^{-1} $.
The phenomenon we are facing is quite difficult to tackle if taken as a whole and we must emit a number of intuitively acceptable hypotheses:
- To simplify the problem, we consider that the diffusion of oxygen particle occurs only in one direction. So $\overrightarrow{J}(M,t) = J(x,t) \overrightarrow{e}_x $. This hypothesis is credible because we seek the maximum penetrance of oxygen. This is why we consider that the diffusion occurs in the line of greatest slope.
- Spatial variations in the density of particles are connected to spatial variations of the vector $\overrightarrow{J}(M,t)$ by the material's equation of conservation in presence of volume distribution of particle source $\sigma (x,t)$ (device which injects or subtracts the particles to the system) :
\[ \frac{\partial n}{\partial t} (x,t) = - \frac{\partial J}{\partial x} (x,t) + \sigma (x,t) \qquad (2) \]
By replacing $(2)$ in $(1)$, we obtain the following equation of diffusion : \[ \boxed{ \forall t>0, \forall x, \bigg( \frac{\partial}{\partial t} - D \frac{\partial^2}{\partial x^2} \bigg) n(x,t) = \sigma (x,t) } \qquad (3) \]
As our lemon is exposed to the ambient air, we stay in steady state where the initial source $ \sigma (x,t_0) $ is equal to $N_0$ the quantity of $O_2$ in the air and $ \sigma (x,t) = 0 $ pour tout $ t > t_0$.
To solve this equation, we use Fourier's analysis and the solution is well known: we have the same expression as the "heat equation"
\[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) \]
Thus we deduce easily that the average dispersion of the particles is given by the variance $\boxed{ \Delta x = \sqrt{2Dt} }$. Using this formula, we deduct that, for example, oxygen will penetrate $3 \times 10^{-3} m$ in $1956.522 s = 32.6082 $ minutes.
We recommend reading the reference [2]. Content is accessible from the first year of university.
The charts below give us a very clear idea of penetrance evaluated over time.
Graphical visualization
We represent in the first figure the solution of the diffusion equation that was previously established. This basically tells us the mean and the average dispersion of particles: it is a probability density given by
\[ \forall x, \forall t>0, n(x,t) = \frac{N_0}{\sqrt{4 \pi D t}} exp \bigg(- \frac{x^2}{4 D t} \bigg) \]
Remember that the purpose of this model is to provide information on the penetration of oxygen into the gel. The figure represents the distance reached by oxygen particles over time. We get it through the formula $ \Delta x = \sqrt{2Dt} $.
It is now important to study how our bacteria will develop in the agar gel. This is well done in this page.
References
[1] A.C. Hulst, H.J.H. Hens, R.M. Buitelaar and J. Tramper, Determination of the effective diffusion coefficient of oxygen in gel materials in relation to gel concentration, Biotechnology Techniques Vol 3 No 3 199-204 (1989).
[2] Vincent Renvoizé, Physique PC-PC*, Cap Prepas, Pearson Education, 2010.
 "
"