Team:Colombia/Stochastic
From 2014.igem.org
Stochastic Model.
Dealing with such a processes, the first possible approach will be to solve the stochastic master equation. The function that satisfies that equation will measure the probability of finding different numbers of molecules of the N different substances at each instant of time. But as you should probably know, this kind of numerical computation will be hard to develop and won’t be efficient. One of the reason is, for example, that, due to the very low probability of occurrence of the events (chemical reactions, ARN transcription, proteins production, …), and the very short time intervals that we should use, most of the time won’t be happening nothing.
For that reason, we decided to use a nice very efficient algorithm proposed by Daniel Gillespie, which is based in a different probability function density: The reaction probability density function. These functions will tell us how much time will pass until the next event occurrence and how this time is distributed. After that we decided which one of the events will occur based on the number of molecules of each species and how they interact with each other.
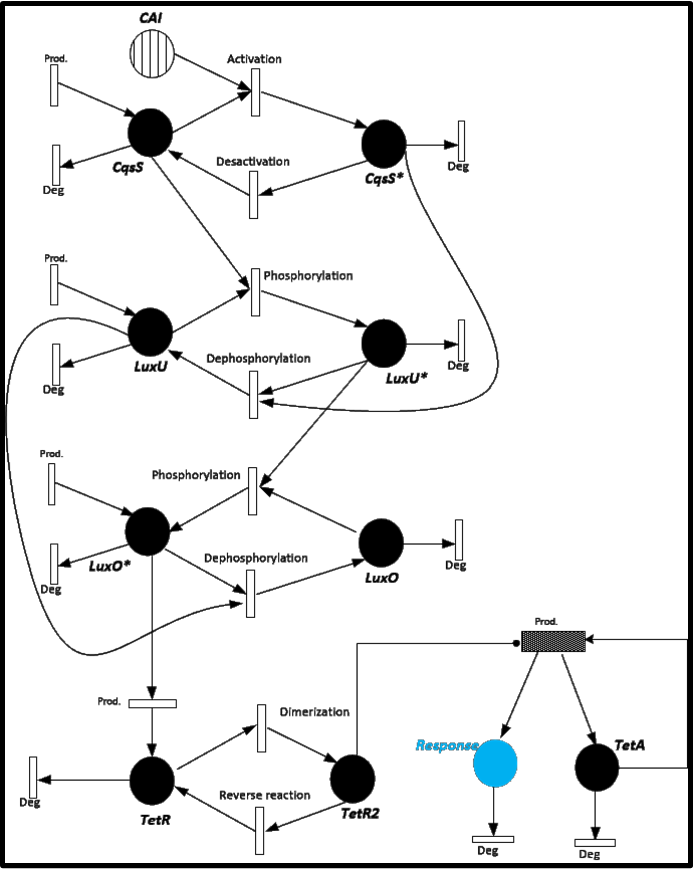
To give you an idea of how does our system works and how will be the events related, we present a Stochastic Petri Net. In Figure 1 we can appreciate the different molecules species interacting between them or undergoing process such as degradation or production.
<
In this case, we have 24 different possible events to take into account. (Table 1)
The time τ between events is calculated by:
Which event will occur is calculated by using another random number R between 0 and 1 in the following way:
Let’s define
Now divide [0,1] in 25 interval such that (Figure 2)
The size of the ith interval depends on the value of n_i.
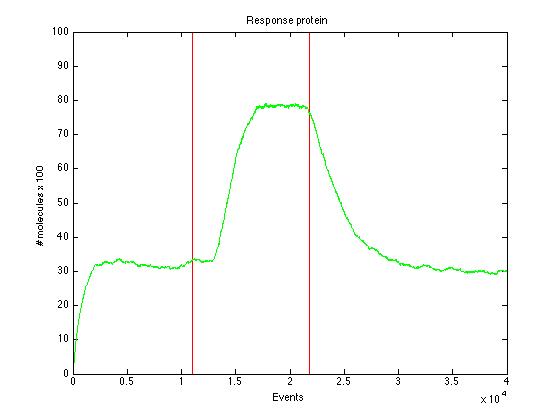
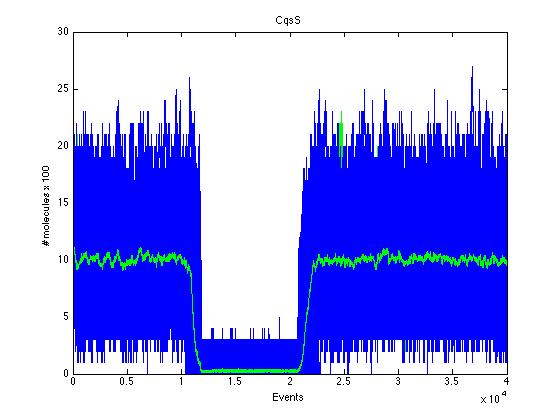
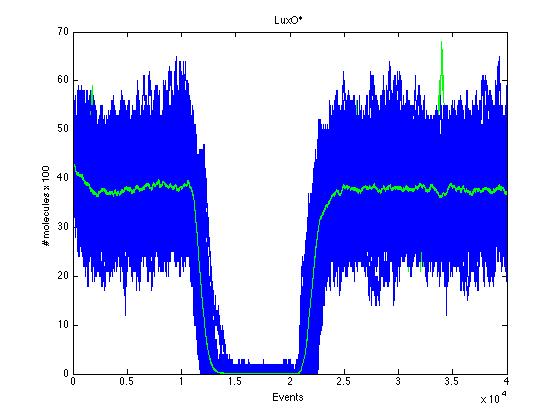
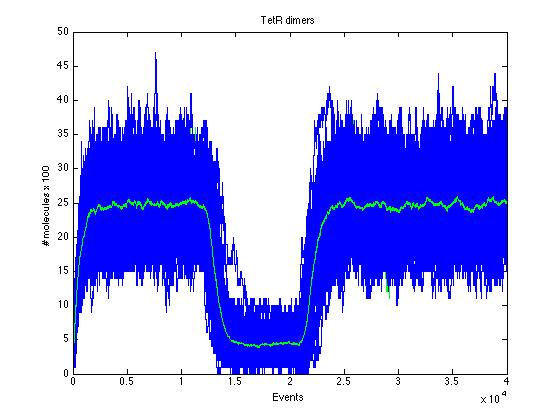
The event that will occur is the one that correspond to in which interval is located the random number R. Results -> Here we present a graphic for each molecule species involved in our system and how it responds to the presence of CAI-1 in the environment. The red line in the Figure 3 represents the amount of CAI-1 molecules in the environment.
The blue lines represent the behavior of each cell and the green line presents the mean behavior of the total population.
 "
"