Team:Waterloo/Math Book/Conjugation
From 2014.igem.org
m (Added staph pictures and captions) |
(Added intro and motivation) |
||
| Line 13: | Line 13: | ||
<div id="MathBook" class="content"> | <div id="MathBook" class="content"> | ||
<ul class="tabs"> | <ul class="tabs"> | ||
| - | <li><a href="# | + | <li><a href="#Intro">Introduction and Motivation</a></li> |
<li><a href="#Model_Formation">Model Formation</a></li> | <li><a href="#Model_Formation">Model Formation</a></li> | ||
<li><a href="#Conjugation_Images">Conjugation Images</a></li> | <li><a href="#Conjugation_Images">Conjugation Images</a></li> | ||
</ul> | </ul> | ||
<div class="tabcontents"> | <div class="tabcontents"> | ||
| - | <div class="anchor" id=" | + | <div class="anchor" id="Intro"> |
| - | <h2> | + | <h2>Introduction and Motivation</h2> |
| + | <p>In order to suppress transcription of the mecA gene, we need a way to deliver our silencing system to the antibiotic resistant cells. To accomplish this, the CRISPRi and sRNA genes are cloned into an engineered conjugative plasmid in closely related cells. The cells with the engineered plasmid are referred to as “donor” cells, and they are introduced to the target population, also known as the “recipients”. The plasmid will transfer from donors to recipients via conjugation, and we refer to these recipient cells with the conjugative plasmid as “transconjugants”. The transconjugants will, in time, be able to retransmit this plasmid. Thus, the system will propagate throughout the infection, thereby disarming the antibiotic resistant cells.</p> | ||
| + | <p>(fig. 1 - diagram of transmission and retransmission of plasmid)</p> | ||
| + | <p>We model the propagation of our plasmid for a number of reasons. Most importantly, we want to determine the optimal time to apply antibiotics to the infection. To do so, we track the total number of donor, recipient, and transconjugant cells and define the “fall time” as the time it takes the number of recipients to reach 10% its initial value. In addition to determining when to apply methicillin, the model can be used to find how large of a conjugation rate is needed and what initial concentration of donor cells is needed to spread the plasmid at a fast enough rate.</p> | ||
| + | <p>Unfortunately, modeling such a system poses quite a bit of difficulty. The primary obstacle is that we consider S. aureus growth on a solid surface (e.g. a lab plate, or on your skin) and not in a well mixed environment. This forces us to abandon more traditional models of conjugation (such as from Levin, Stewart, and Rice) and develop a spatial model instead. We took two main approaches to developing such a model: an agent-based model (ABM), and a partial differential equation (PDE) model.</p> | ||
| + | <p>The ABM is a stochastic simulation of conjugation through a population of donor and recipient cells. The main advantages of this model are that it accounts for randomness of plasmid transfer, as well as likely maintaining accuracy on small-scale areas. Its main drawback is that it is computationally expensive to model a large number of cells, and thus cannot model populations on large scales.</p> | ||
| + | <p>The PDE Model addresses large scale populations through deterministic methods. Being a differential equation system, a wide variety of mathematical tools to analyze the system are readily available, and it is more computationally efficient than the Agent-Based Model.</p> | ||
</div> | </div> | ||
| + | |||
| + | |||
<div class="anchor" id="Model_Formation"> | <div class="anchor" id="Model_Formation"> | ||
<h2>Model Formation</h2> | <h2>Model Formation</h2> | ||
</div> | </div> | ||
| + | |||
| + | |||
<div class="anchor" id="Conjugation_Images"> | <div class="anchor" id="Conjugation_Images"> | ||
<h2>Conjugation Images</h2> | <h2>Conjugation Images</h2> | ||
Revision as of 02:13, 18 October 2014

Math Book: Conjugation
Introduction and Motivation
In order to suppress transcription of the mecA gene, we need a way to deliver our silencing system to the antibiotic resistant cells. To accomplish this, the CRISPRi and sRNA genes are cloned into an engineered conjugative plasmid in closely related cells. The cells with the engineered plasmid are referred to as “donor” cells, and they are introduced to the target population, also known as the “recipients”. The plasmid will transfer from donors to recipients via conjugation, and we refer to these recipient cells with the conjugative plasmid as “transconjugants”. The transconjugants will, in time, be able to retransmit this plasmid. Thus, the system will propagate throughout the infection, thereby disarming the antibiotic resistant cells.
(fig. 1 - diagram of transmission and retransmission of plasmid)
We model the propagation of our plasmid for a number of reasons. Most importantly, we want to determine the optimal time to apply antibiotics to the infection. To do so, we track the total number of donor, recipient, and transconjugant cells and define the “fall time” as the time it takes the number of recipients to reach 10% its initial value. In addition to determining when to apply methicillin, the model can be used to find how large of a conjugation rate is needed and what initial concentration of donor cells is needed to spread the plasmid at a fast enough rate.
Unfortunately, modeling such a system poses quite a bit of difficulty. The primary obstacle is that we consider S. aureus growth on a solid surface (e.g. a lab plate, or on your skin) and not in a well mixed environment. This forces us to abandon more traditional models of conjugation (such as from Levin, Stewart, and Rice) and develop a spatial model instead. We took two main approaches to developing such a model: an agent-based model (ABM), and a partial differential equation (PDE) model.
The ABM is a stochastic simulation of conjugation through a population of donor and recipient cells. The main advantages of this model are that it accounts for randomness of plasmid transfer, as well as likely maintaining accuracy on small-scale areas. Its main drawback is that it is computationally expensive to model a large number of cells, and thus cannot model populations on large scales.
The PDE Model addresses large scale populations through deterministic methods. Being a differential equation system, a wide variety of mathematical tools to analyze the system are readily available, and it is more computationally efficient than the Agent-Based Model.
Model Formation
Conjugation Images

Sufficient conjugation rate at t = 0h
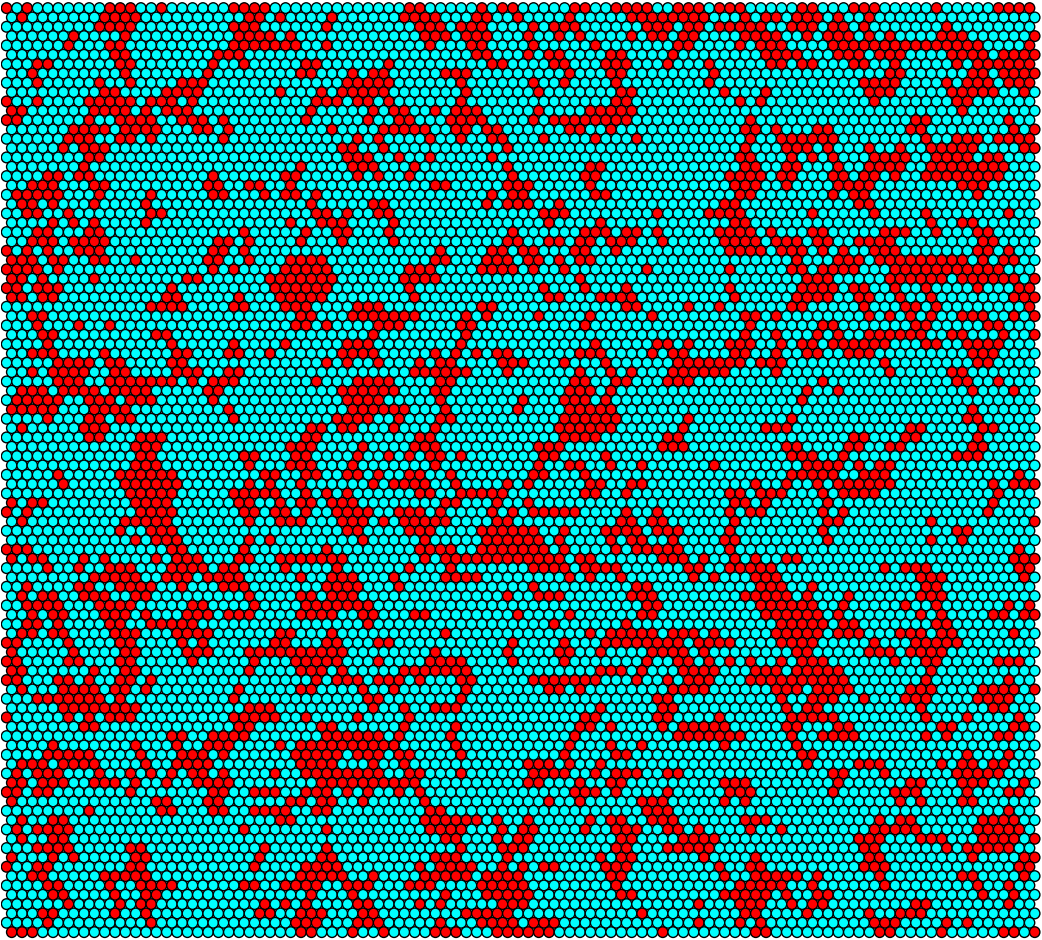
Sufficient conjugation rate at t = 6h

Sufficient conjugation rate at t = 12h

Sufficient conjugation rate at t = 18h

Sufficient conjugation rate at t = 24h

Sufficient conjugation rate population for 10-by-10 grid

Sufficient conjugation rate population for 100-by-100 grid

S. aureus conjugation rate at t = 0h

S. aureus conjugation rate at t = 6h

S. aureus conjugation rate at t = 12h

S. aureus conjugation rate at t = 18h

S. aureus conjugation rate at t = 24h
 "
"




