Team:Waterloo/Math Book/Conjugation
From 2014.igem.org

Math Book: Conjugation
Introduction and Motivation
In order to suppress transcription of the mecA gene, we need a way to deliver our silencing system to the antibiotic resistant cells. To accomplish this, the CRISPRi and sRNA genes are cloned into an engineered conjugative plasmid in closely related cells. The cells with the engineered plasmid are referred to as “donor” cells, and they are introduced to the target population, also known as the “recipients”. The plasmid will transfer from donors to recipients via conjugation, and we refer to these recipient cells with the conjugative plasmid as “transconjugants”. The transconjugants will, in time, be able to retransmit this plasmid. Thus, the system will propagate throughout the infection, thereby disarming the antibiotic resistant cells.

Bacterial conjugation
We model the propagation of our plasmid for a number of reasons. Most importantly, we want to determine the optimal time to apply antibiotics to the infection. To do so, we track the total number of donor, recipient, and transconjugant cells and define the “fall time” as the time it takes the number of recipients to reach 10% its initial value. In addition to determining when to apply methicillin, the model can be used to find how large of a conjugation rate is needed and what initial concentration of donor cells is needed to spread the plasmid at a fast enough rate.
Unfortunately, modeling such a system poses quite a bit of difficulty. The primary obstacle is that we consider S. aureus growth on a solid surface (e.g. a lab plate, or on your skin) and not in a well mixed environment. This forces us to abandon more traditional models of conjugation (such as from Levin, Stewart, and Rice) and develop a spatial model instead. We took two main approaches to developing such a model: an agent-based model (ABM), and a partial differential equation (PDE) model.
The ABM is a stochastic simulation of conjugation through a population of donor and recipient cells. The main advantages of this model are that it accounts for randomness of plasmid transfer, as well as likely maintaining accuracy on small-scale areas. Its main drawback is that it is computationally expensive to model a large number of cells, and thus cannot model populations on large scales.
The PDE Model addresses large scale populations through deterministic methods. Being a differential equation system, a wide variety of mathematical tools to analyze the system are readily available, and it is more computationally efficient than the Agent-Based Model.
Agent-Based Model
Overview
We have developed a novel model for bacterial conjugation on flat surfaces. By treating each bacterium as an “agent” that has properties associated with its type (either Donor or Recipient), and letting the group of agents interact over a prescribed period of time, one can make qualitative and quantitative conclusions about their behavior.
The model is based on the idea of having hexagonal cells that each may or may not be occupied by a donor (e.g. modified S. epidermidis) or a recipient (e.g. MRSA). An individual bacterium may divide into an empty neighboring cell and if the cell is a donor, conjugate with an adjacent recipient. We assume that the conjugative plasmid represses methicillin-resistance 100% (i.e. all donor cells will die upon introduction of antibiotic).
The hexagonal grid was used over a traditional square grid because hexagons offer more routes for conjugation and division to occur, as well as the fact that hexagons form a tighter packing structure than squares. Because bacteria are capable of very tight packing on flat surfaces, the hexagonal framework more accurately captures interaction between neighboring bacteria - an important consideration when modeling conjugation.
Algorithm
Before outlining our algorithm, it is important to explicitly state the general assumptions we made in the ABM:
- The flat surface is treated as a 2D hexagonal grid (of size n x n), and refer to each grid location as a hex
- Each hex may be occupied by at most one bacterium
- We do not distinguish between transconjugants original donors
- Donors and Recipients are both able to divide
- Donors may conjugate with recipients, after which the recipient becomes a donor
- A cell may divide if there is an empty adjacent hex
- A donor may conjugate if there is a recipient in an adjacent hex
- The natural death rate of cells is negligible (i.e. cells don’t die)
- All cells are stationary, so population “movement” occurs through division into neighboring cells
The scripts used to run this model were written in Python and follow a very basic structure:

Flowchart for the Agent-Based Model algorithm
Technical assumptions and details:
- The algorithm uses weighted uniform distributions (about specified parameters) for conjugation and division
- Donors lose half of their plasmids when they divide
- We do not distinguish between transconjugants original donors
- Cells enter a paused state after they divide or conjugate for a certain amount of time, allowing them to “recharge”
A few potential issues:
- Donors are given a chance to conjugate before they are given a chance to divide
- Cells are equally likely to divide, whether it's 100 turns after they're created or 0 turns
- We iterate through the grid in numerical order, which may lead to an “unnatural” sequence of cell interactions (i.e. inaccuracy). As the simulation “turn time” decreases, the resulting inaccuracy from this behaviour should become negligible
- The lack of cell death does not seem realistic in a living body
Parameters
| Parameter | Model Value | Experimental Value | Units | Comments |
| Agent division frequency* | Donor: 0.5, Recipient: 0.5 | S. aureus: 1.43, E. coli: 3.31 | divisions/h | Chung, 2006, and Reshes, 2008 |
| Agent conjugation period* | 10** | S. aureus: 3.1*107, E. Coli: 4.8*104 | h/conjugation event | Projan, 1989, and Phornphisutthimas, 2007 |
| Agent division delay time | Donor: 0.5, Recipient: 0.5 | N/A | h | after division, the time until the cell can divide again |
| Agent conjugation delay time | 0.25 | N/A | h | after conjugation, the time until the donor can conjugate again |
| Agent cell radius | 1 | S. aureus: 1, E. Coli 1 | µm |
* These values are treated as averages in the code, with associated probability distributions.
** The conjugation period row is noteworthy because of the somewhat significant discrepancy between the model value we chose and sample values found in literature. We chose to use a value of 10 hours per conjugation event because it was a suitable order of magnitude to display conjugation occurring within a 24 hour simulation. We welcome input regarding experimental conjugation rates, as there seems to be a lack of applicable literature, and the experimental values we did find are surprisingly large.
Results
By specifying a grid size (n) and a simulation time (T), our model is able to output time-series data and images at of the grid during each step of time.

Idealized conjugation rate population for 10-by-10 grid

Idealized conjugation rate population for 100-by-100 grid
For the 100-by-100 grid we have that Donors are turquoise, Recipients are red, and empty hexes are white.

Idealized conjugation rate at t = 0h
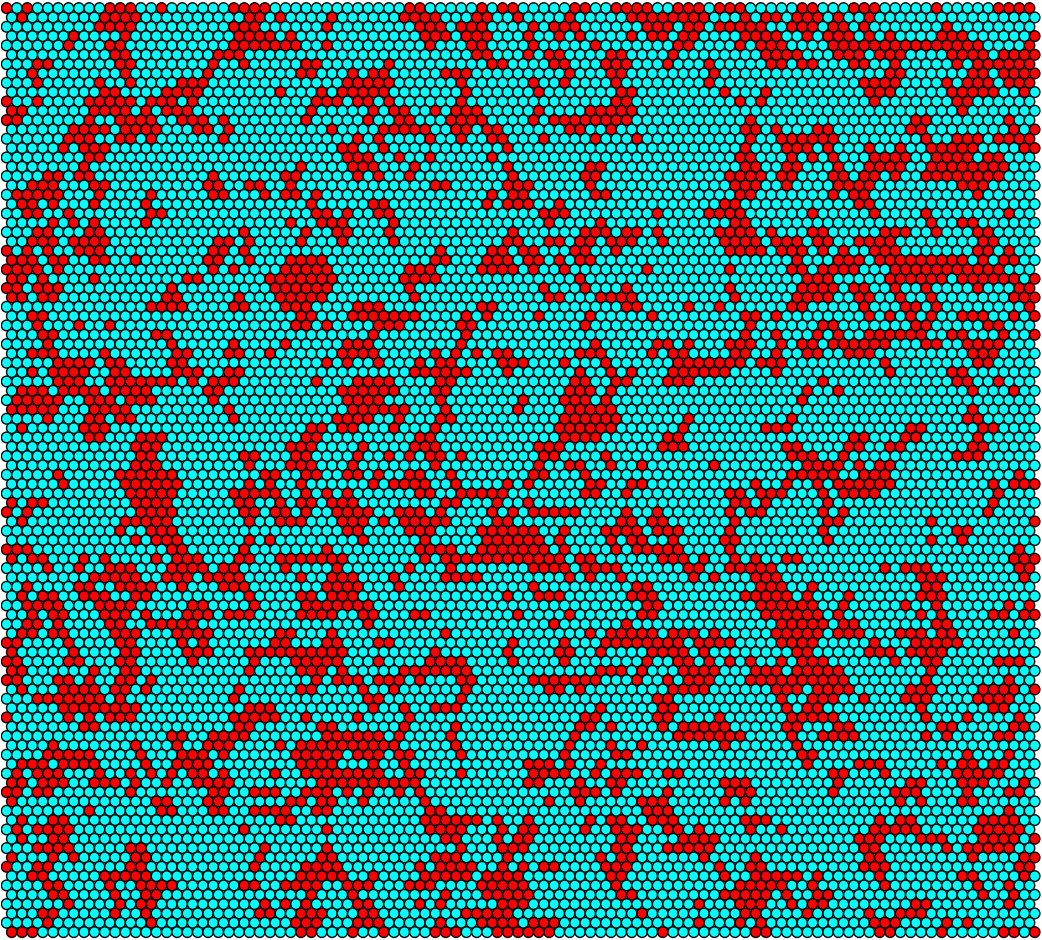
Idealized conjugation rate at t = 6h

Idealized conjugation rate at t = 12h

Idealized conjugation rate at t = 18h

Idealized conjugation rate at t = 24h
PDE Model
Overview
We seek an alternative to the agent-based model which can verify its results and run simulations on an even larger scale. To do this we developed a PDE model which tracks three species of cells through time: donors, recipients, and transconjugants. The silencing system itself is able to move by being carried by diffusion as the donors move and then the plasmid spreads locally through conjugation. d is the diffusivity, P is the population of interest, N is the total concentration of cells. The reason it looks so strange is that we are using diffusion to approximate vegetative growth of the cell. The outward growth of one population of cells - for example the donors - will depend on the total population of cells surrounding it and not just the surrounding donors. As such we take the Laplacian of N and then normalize it by multiplying by the fraction in that population.
Next, each of the populations will undergo logistic growth so we add a logistic growth term to each DE. We assume that each cell has the same growth rate r and that interspecific and intraspecific competition are the same.
Finally, the recipient cells will be converted to transconjugants over time, so we introduce a conjugation term that will allow donors and transconjugants to convert recipients to transconjugants. This term comes directly from Levin, 1979.
System of PDE's
Since there are three species we are concerned with there are three PDEs to our system. Let D represent the concentration of donors, R the concentration of recipients, and T the concentration of transconjugants. Each equation will have a diffusion and logistic growth term but the recipients and transconjugants will receive a third term for conjugation.

The PDE Model system of equations
Parameters
| Parameter | Value | Description | Comments |
| d | 0.001 m2/h | Diffusion coefficient | Arbitrary, to allow for some movement of cells as they grow |
| 0.5 h | Doubling time | ||
| rD, rR, rT | 1.39 | Donor, recipient, and transconjugant growth rates | ln(2)/ doubling time |
| K | 2.887*1011 cells/m2 | Carrying capacity | Based on packing circles in a hexagonal pattern with cell radii of 1 µm. K = (π/√12)/(π*(cell radius)2). Chang and Wang, 2010 |
| f | 10 h/conjugation event | Conjugation period | |
| λ | 6.928*10-13 (conjugation events*m2)/(h*cells) | Conjugation rate | 2/(K*f) |
Results
We simulate a square area with size 1 cm2 using a simple finite difference scheme (first-order forward difference for time, second-order central difference for space). We use 100 grid points in each dimension so dx=dy=0.01 cm and then choose dt so that dt=(dx2+dy2)/10d where d=0.001 is the diffusivity. This provides results very similar to the ABM.

Heatmaps describing the spatial distribution of each type of cell

A plot of the populations that show similar results to those of the Agent-Based Model
Remarks and Future Work
We regard the ABM as our main conjugation model, due to its accuracy. Unfortunately, its excessive runtime limits the amount of analysis that can be done on it. In order to conduct more analysis on the spread of our conjugative plasmid through the target population, we are planning to use the ABM to validate the PDE model. Initial, small scale results for the ABM (population size of < 100 000 bacteria) seem to correspond well to the PDE results.
Once we fully validate the results from the PDE model, we can begin to answer interesting design questions. The core question we hope to answer is: “After introducing our modified donor cells into a localized MRSA infection, when is the best time to introduce antibiotics?”
It’s a tricky question to answer, because once we apply antibiotic all the donors (which contain the silencing plasmid) will die, requiring the application of fresh donors. If we get to that stage in the modelling, we plan to use techniques from Optimal Control Theory to find the treatment plan that minimizes the amount of time needed to eliminate the MRSA infection, thereby minimizing negative health effects for the patient.
References
| [1]D. Bikard et al. “Programmable repression and activation of bacterial gene expression using an engineered CRISPR-Cas system”. In: Nucleic Acids Res. 41.15 (Aug. 2013), pp. 7429–7437. |
| [2]Florian Brandt et al. “The Native 3D Organization of Bacterial Polysomes”. In: Cell 136.2 (2009), pp. 261 –271. issn: 0092-8674. doi: 10.1016/j.cell.2008.11.016. |
| [3]A. G. Cheng, D. Missiakas, and O. Schneewind. “The giant protein Ebh is a determinant of Staphylococcus aureus cell size and complement resistance”. In: J. Bacteriol. 196.5 (2014), pp. 971–981. |
| [4]A. L. Cheung, K. Nishina, and A. C. Manna. “SarA of Staphylococcus aureus binds to the sarA promoter to regulate gene expression”. In: J. Bacteriol. 190.6 (Mar. 2008), pp. 2239–2243. |
| [5]G. Domingue, J. W. Costerton, and M. R. Brown. “Bacterial doubling time modulates the effects of opsonisation and available iron upon interactions between Staphylococcus aureus and human neutrophils”. In: FEMS Immunol. Med. Microbiol. 16.3-4 (Dec. 1996), pp. 223–228. |
| [6]S. Michalik et al. “Life and death of proteins: a case study of glucose-starved Staphylococcus aureus”. In: Mol. Cell Proteomics 11.9 (Sept. 2012), pp. 558–570. |
| [7]R. Milo et al. “BioNumbers-the database of key numbers in molecular and cell biology”. In: Nucleic Acids Res. 30 (Jan. 2010), pp. D750–D753. url: http://bionumbers.hms.harvard.edu/bionumber.aspx?id=107869}. |
| [8]L. S. Qi et al. “Repurposing CRISPR as an RNA-guided platform for sequence-specific control of gene expression”. In: Cell 152.5 (Feb. 2013), pp. 1173–1183. |
| [9]C. Roberts et al. “Characterizing the effect of the Staphylococcus aureus virulence factor regulator, SarA, on log-phase mRNA half-lives”. In: J. Bacteriol. 188.7 (Apr. 2006), pp. 2593–2603. doi: 10.1128/JB.188.7.2593-2603.2006 |
| [10]Marlena Siwiak and Piotr Zielenkiewicz. “Transimulation - Protein Biosynthesis Web Service”. In: PLoS ONE 8.9 (Sept. 2013), e73943. doi: 10.1371/journal.pone.0073943. |
| [11]S.H. Sternberg et al. “DNA interrogation by the CRISPR RNA-guided endonuclease Cas9”. In: Nature 7490 (2014), 6267. doi: 10.1038/nature13011. url: http://www.nature.com/nature/journal/v507/n7490/full/nature13011.html. |
| [12]Freiburg iGEM Team. dCas9. BBa K1150000 Standard Biological Part. 2013. url: http://parts.igem.org/Part:BBa_K1150000. |
| [13]UCSF iGEM Team. Operation CRISPR: Decision Making Circuit Model. 2013. url: https://2013.igem.org/Team:UCSF/Modeling. |
| [14]Jian-Qiu Wu and Thomas D. Pollard. “Counting Cytokinesis Proteins Globally and Locally in Fission Yeast”. In: Science 310.5746 (2005), pp. 310–314. doi: 10.1126/science.1113230. |
| [15]Jianfang Jia and Hong Yue. “Sensitivity Analysis and Parameter Estimation of Signal Transduction Pathways Model”. In: Proceedings of the 7th Asian Control Conference (Aug. 2009), pp. 1357–1362. |
| [16]Fi-John Chang and J. W. Delleur. “Systematic Parameter Estimation Of Watershed Acidification Model”. In: Hydrological Processes 6. (1992), pp. 29–44. doi: 10.1002/hyp.3360060104. |
| [17]Aiba, H. (2007). Mechanism of RNA silencing by Hfq-binding small RNAs. Current opinion in microbiology, 10 (2), 134-139. |
| [18]Horstmann, N., Orans, J., Valentin-Hansen, P., Shelburne, S. A., & Brennan, R. G. (2012). Structural mechanism of Staphylococcus aureus Hfq binding to an RNA A-tract. Nucleic acids research, gks809. |
| [19]Eyraud, A., Tattevin, P., Chabelskaya, S., & Felden, B. (2014). A small RNA controls a protein regulator involved in antibiotic resistance in Staphylococcus aureus. Nucleic acids research, gku149. |
| [20]Shimoni, Y., Friedlander, G., Hetzroni, G., Niv, G., Altuvia, S., Biham, O., & Margalit, H. (2007). Regulation of gene expression by small non‐coding RNAs: a quantitative view. Molecular Systems Biology, 3 (1) |
| [21]Fender, A., Elf, J., Hampel, K., Zimmermann, B., & Wagner, E. G. H. (2010). RNAs actively cycle on the Sm-like protein Hfq. Genes & Development, 24 (23),2621-2626. |
| [22] Swain, P. S. (2004). Efficient attenuation of stochasticity in gene expression through post-transcriptional control. Journal of molecular biology, 344 (4),965-976. |
| [23] Hussein, R., & Lim, H. N. (2012). Direct comparison of small RNA and transcription factor signaling. Nucleic acids research, 40 (15), 7269-7279. |
| [24] Levin, B.R., Stewart, F.M. and Rice, V.A. 1979. “The Kinetics of Conjugative Plasmid Transmission: Fit of a Simple Mass Action Model.” In: Plasmid. 2. pp. 247-260. |
| [25]Projan, S.J. and Archer, G.L. 1989. “Mobilization of the Relaxable Staphylococcus aureus Plasmid pC221 by the Conjugative Plasmid pGO1 Involves Three pC221 Loci.” In: Journal of Bacteriology. pp. 1841-1845. |
| [26]Phornphisutthimas, S., Thamchaipenet, A., and Panijpan, B. 2007. “Conjugation in Escherichia coli.” In: The International Union of Biochemistry and Molecular Biology. 35. 6. pp. 440-445. |
| [27]Phornphisutthimas, S., Thamchaipenet, A., and Panijpan, B. 2007. “Conjugation in Escherichia coli.” In: The International Union of Biochemistry and Molecular Biology. 35. 6. pp. 440-445. |
| [28]P Chung P., McNamara P.J., Campion J.J., Evans M.E. 2006. “Mechanism-based pharmacodynamic models of fluoroquinolone resistance in Staphylococcus aureus.” In: In: Antimicrobial Agents Chemotherapy. 50. pp. 2957-2965. |
| [29] Chang H., Wang L. “A Simple Proof of Thue's Theorem on Circle Packing” In: arXiv:1009.4322v1. |
 "
"




