Model

The Quorum sensing module is mainly involved in receiving signals from the parents.

Chemical Species

• Bxb1: integrase that can fold into two conformations called Bxb1a and Bxb1b. Even if those conformations have the same sequence of amino acids, their tertiary structure is different. As it is experimentally difficult to differentiate these two conformations, we chose to regroup them under the specie Bxb1.

• ΦC31: integrase that can fold into two conformations called ΦC31a and ΦC31b. Similarly to Bxb1, we chose to factorize these two conformations under the specie ΦC31.

• DBxb1: dimer of Bxb1. Bxb1a (respectively Bxb1b) forms a dimer DBxb1a (respectively DBxb1b). To be coherent, dimers re not differentiated depending on their spatial configuration.

• DΦC31: dimer of ΦC31. ΦC31a (respectively ΦC31b) forms a dimer DΦC31a (respectively DΦC31b). The different spatial configuration are not taken into account.

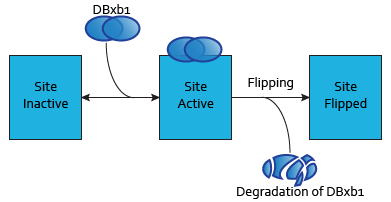
Modelization of DNA-binding sites

Each dimer of integrases can specifically bind to a DNA binding site. As the flipping is irreversible, these DNA binding sites can be three possible states:

• SI_{IntegraseName}: inactive DNA binding site. No dimer is bound to this site, which has never been flipped.

• SA_{IntegraseName}: active DNA binding site. A dimer is to this site.

• SF_{IntegraseName}: flipped DNA binding site. This DNA binding site has been used by a flipping.

The three different states of DBxb1-DNA binding sites.

Reactions

For Bxb1

$$ \begin{align} Bxb1 + Bxb1 &\leftrightarrow DBxb1 \\ DBxb1 + SI_{Bxb1} & \leftrightarrow SA_{Bxb1}\\ Bxb1 &\rightarrow \\ DBxb1 &\rightarrow \end{align}$$

For ΦC31

\begin{align} \phi C31 + \phi C31 &\leftrightarrow D\phi C 31 \\ D\phi C 31 + SI_{\phi C31} & \leftrightarrow SA_{\phi C31}\\ \phi C31 &\rightarrow \\ D\phi C31 &\rightarrow \end{align}

Differential Equations

Applying mass action kinetic laws, we obtain the following set of differential equations.

$$\frac{d[Bxb1]}{dt}=-2 k_{dimBxb1}[Bxb1]^2+ 2 k_{-dimBxb1}[DBxb1]-d_{Bxb1}[Bxb1]$$

$$\frac{d[DBxb1]}{dt}=-k_{DNABxb1}[DBxb1][SI_{Bxb1}]+k_{-DNABxb1}[SA_{Bxb1}]+k_{dimBxb1}[Bxb1]^2-k_{-dimBxb1}[DBxb1a]-d_{DBxb1}[DBxb1]$$

$$\frac{d[SA_{Bxb1}]}{dt}=k_{DNABxb1}[DBxb1][SI_{Bxb1}]-k_{-DNABxb1}[SA_{Bxb1}]$$

Characterization

Data

Assumptions

Parameter fitting

Range of validity of the assumptions

Characterization

Data

Assumptions

Parameter fitting

Range of validity of the assumptions