Team:Oxford/Results
From 2014.igem.org
(Difference between revisions)
| Line 183: | Line 183: | ||
We also developed the following models: <br><br> | We also developed the following models: <br><br> | ||
1. Microcompartment Shape Model: (see <a href="https://2014.igem.org/Team:Oxford/what_are_microcompartments?#show2" target="_blank">'Predicting the microcompartment structure'</a>) a model that simulates the effect of random point deviations in the microcompartment structure from the perfect icosahedral structure seen in carboxysomes.<br><br> | 1. Microcompartment Shape Model: (see <a href="https://2014.igem.org/Team:Oxford/what_are_microcompartments?#show2" target="_blank">'Predicting the microcompartment structure'</a>) a model that simulates the effect of random point deviations in the microcompartment structure from the perfect icosahedral structure seen in carboxysomes.<br><br> | ||
| + | <img src=" https://static.igem.org/mediawiki/2014/7/7f/Microcompartment_shape_2.jpg " max-height="500" style="float:right;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;"/><br> | ||
| + | <strong>Figure 1</strong> | ||
| + | <br> | ||
| + | The output of the microcompartment shape model is a simulated microcompartment structure (blue) plotted alongside the perfect icosahedral structure of a carboxysome (red) which we used as a starting point for predicting the geometric structure of a microcompartment. | ||
| + | <br><br> | ||
| + | |||
2. Prediction of number of enzymes per microcompartment (see <a href="https://2014.igem.org/Team:Oxford/what_are_microcompartments?#show4" target="_blank">'Modelling the number of enzymes in a microcompartment'</a>) By modelling enzymes as ellipsoids with axis length dependent on the maximum x,y and z dimensions of our enzyme complexes, this was broken down into the well-documented sand-packing problem. This enabled us to predict the maximum theoretical number of enzymes that can be packed into a microcompartment.<br><br> | 2. Prediction of number of enzymes per microcompartment (see <a href="https://2014.igem.org/Team:Oxford/what_are_microcompartments?#show4" target="_blank">'Modelling the number of enzymes in a microcompartment'</a>) By modelling enzymes as ellipsoids with axis length dependent on the maximum x,y and z dimensions of our enzyme complexes, this was broken down into the well-documented sand-packing problem. This enabled us to predict the maximum theoretical number of enzymes that can be packed into a microcompartment.<br><br> | ||
3. Effect of microcompartments on collision rates (see <a href="https://2014.igem.org/Team:Oxford/why_do_we_need_microcompartments?#show3" target="_blank">'Microcompartment rate of collision model'</a>) By using our stochastic diffusion models and discretizing the motion of our simulated particles, this compared the rate of collision of two particles when spatially constrained within a microcompartment versus in unconstrained motion.<br><br> | 3. Effect of microcompartments on collision rates (see <a href="https://2014.igem.org/Team:Oxford/why_do_we_need_microcompartments?#show3" target="_blank">'Microcompartment rate of collision model'</a>) By using our stochastic diffusion models and discretizing the motion of our simulated particles, this compared the rate of collision of two particles when spatially constrained within a microcompartment versus in unconstrained motion.<br><br> | ||
| + | <img src=" https://static.igem.org/mediawiki/2014/e/e1/Collision_diffusion_with_microcompartment.jpg | ||
| + | " max-height="500" style="float:right;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;"/><br> | ||
| + | |||
| + | <strong>Figure 2</strong> | ||
| + | <br> | ||
| + | We have plotted the trajectories of two different molecules along random, stochastically driven discretized paths. What we illustrate here is that the rate of collision (marked in red) is substantially increased through the use of spatial constraints. | ||
| + | <br><br> | ||
| + | |||
4. Stochastic diffusion of formaldehyde within microcompartments (see <a href="https://2014.igem.org/Team:Oxford/why_do_we_need_microcompartments?#show5" target="_blank">'Modelling the diffusion of formaldehyde inside the microcompartment'</a>) Stochastic diffusion of formaldehyde within cell: Building on the stochastic diffusion models developed previously, we then predicted how the concentration of formaldehyde within a cell would change over time given the restrictions imposed by the microcompartment. | 4. Stochastic diffusion of formaldehyde within microcompartments (see <a href="https://2014.igem.org/Team:Oxford/why_do_we_need_microcompartments?#show5" target="_blank">'Modelling the diffusion of formaldehyde inside the microcompartment'</a>) Stochastic diffusion of formaldehyde within cell: Building on the stochastic diffusion models developed previously, we then predicted how the concentration of formaldehyde within a cell would change over time given the restrictions imposed by the microcompartment. | ||
<br><br> | <br><br> | ||
5. Star-peptide model (see <a href="https://2014.igem.org/Team:Oxford/alternatives_to_microcompartments#show2" target="_blank">'The Star-Peptide Model'</a>) Our major collaboration with Unimelb iGEM involved modelling the effect of attaching multiple enzymes to a star peptide. This built upon the stochastic diffusion models developed earlier and represents an alternative method of reducing toxic intermediate accumulation to microcompartments. | 5. Star-peptide model (see <a href="https://2014.igem.org/Team:Oxford/alternatives_to_microcompartments#show2" target="_blank">'The Star-Peptide Model'</a>) Our major collaboration with Unimelb iGEM involved modelling the effect of attaching multiple enzymes to a star peptide. This built upon the stochastic diffusion models developed earlier and represents an alternative method of reducing toxic intermediate accumulation to microcompartments. | ||
<br><br> | <br><br> | ||
| + | <img src=" https://static.igem.org/mediawiki/2014/1/1b/Star_protein_length_vs_rate_loglog.jpg | ||
| + | " max-height="500" style="float:right;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;"/><br> | ||
| - | + | <strong>Figure 3</strong> | |
| - | <strong>Figure | + | |
<br> | <br> | ||
| - | + | Plotted here is the logarithmic relationship between star peptide bond length and reaction rate. This was simulated for Melbourne iGEM and suggests that the rate of reaction will be inversely proportional to average peptide length to the power of four. | |
<br><br> | <br><br> | ||
Revision as of 02:29, 18 October 2014
 "
"


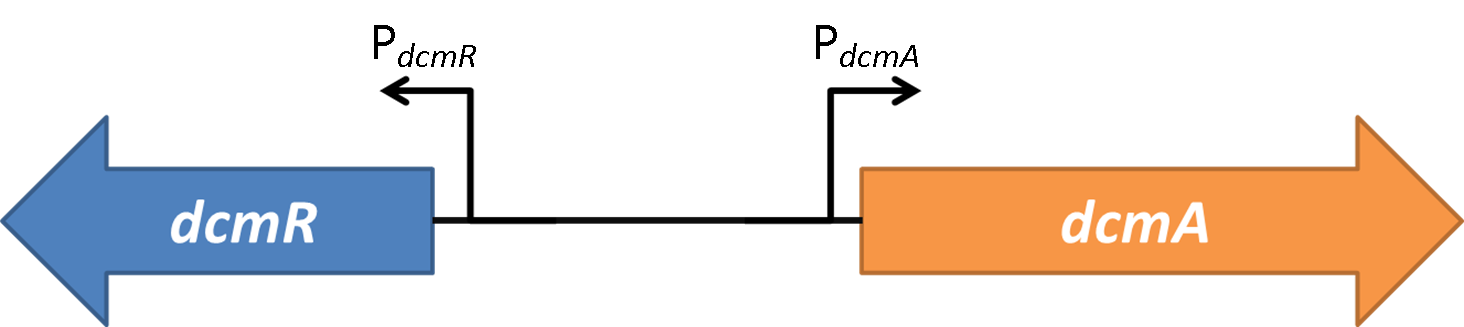





 Figure 2
Figure 2