Team:LMU-Munich/Project/Modeling

From 2014.igem.org

(Difference between revisions)
(bugfixing & typos)
Line 72: Line 72:
<html>
<html>
-
</section>
 
</div>
</div>
 +
</section>
       <section class="accordion">
       <section class="accordion">
           <div>
           <div>
Line 83: Line 83:
-
<html></article></div></html>
 
We implemented the model in C++, making extensive use of the ''Boost'' libraries for numerical integration, among other things. In addition,
We implemented the model in C++, making extensive use of the ''Boost'' libraries for numerical integration, among other things. In addition,
Line 108: Line 107:
Each bacterium will then swim forward (run) or change its orientation (tumble) dependent on the phosphorylation level of CheY.
Each bacterium will then swim forward (run) or change its orientation (tumble) dependent on the phosphorylation level of CheY.
 +
<html>
 +
</div>
 +
</section>
 +
    <section>
 +
<div>
 +
</html>
=== Results & Discussion ===
=== Results & Discussion ===
 +
Line 123: Line 129:
For safety issues we want BaKillus to autoinduce apoptosis after successful completion of his task. This can be achieved by shutting down the production of resistance providing anti-toxin proteins. (see: [https://2014.igem.org/Team:LMU-Munich/Project/Bakillus#suicide Suicide-Switch]) Still, BaKillus must produce sufficients amounts of toxins before inducing apotosis. Therefor, the negative feedback, which eventually stops production of anti-toxin must be sufficiently delayed to provide a sufficiently long timeframe for toxin production. However, as simple as this idea might sound in theory, robust practical implementation of such a module requires precise finetuning of the kinetics of the respective signalling cascade.  In this model we tried to assess whether the inclusion of a secondary sigma factor could theoretically enhance the efficiency of the killing mechanism.
For safety issues we want BaKillus to autoinduce apoptosis after successful completion of his task. This can be achieved by shutting down the production of resistance providing anti-toxin proteins. (see: [https://2014.igem.org/Team:LMU-Munich/Project/Bakillus#suicide Suicide-Switch]) Still, BaKillus must produce sufficients amounts of toxins before inducing apotosis. Therefor, the negative feedback, which eventually stops production of anti-toxin must be sufficiently delayed to provide a sufficiently long timeframe for toxin production. However, as simple as this idea might sound in theory, robust practical implementation of such a module requires precise finetuning of the kinetics of the respective signalling cascade.  In this model we tried to assess whether the inclusion of a secondary sigma factor could theoretically enhance the efficiency of the killing mechanism.
-
In the following we will compare two different models, one including only one sigma factor and one including two sigma factors. The models will be compared based on a fitness function which describes the difference between the toxin and antitoxin production over time. This should provide a measure of the effective number of produced molecules toxin molecules.  
+
In the following we will compare two different models, one including only one sigma factor and one including two sigma factors. The models will be compared based on a fitness function which describes the difference between the toxin and antitoxin production over time. This should provide a measure of the effective number of produced toxin molecules.  
=== Basic Model ===
=== Basic Model ===

Revision as of 16:04, 17 October 2014

 

Modeling

Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet.

Chemotaxis

Motivation

To stay true to its title 'pathogen-hunting microbe', BaKillus should ideally be able to swim towards its prey via chemotaxis. However, the ability to react to an AIP- or CSP-gradient requires the introduction of a chimeric receptor into Bacillus subtilis. Chemotaxis receptors are quite complex and can, for example, take different methylation states to allow for attenuation of the chemotactic response. This complexity puts the construction of a custom receptor beyond the scope of an iGEM project.

To evaluate how a hypothetical chemotactic BaKillis would act in an experimental setting, we developed a model to simulate the movement of chemotactic hunters in response to an attractant gradient produced by a growing colony of prey bacteria.

Overview

Our multi-scale hybrid model essentially consists of 3 components: growth of prey bacteria (algebraic model), diffusion of attractant molecules (spatial partial differential equation) and chemotactic behavior of the hunter bacteria (stochastic spatial agent model coupled to differential equations for internal state with a stochastic driving force). All these processes take place in a defined geometric space (representing, for example, a microfluidic device). The experimental scenario we wish to capture in our model is the following: a colony of prey bacteria is spotted onto the arena, growing in place and producing attractant molecules. A fixed population of hunter bacteria is placed into the arena as well. Their reaction (biased movement) to the building attractant gradient is what we seek to observe.

Growth of prey

The prey bacteria will grow on a population level, according to a logistic growth curve with explicit solutions (ref!):

\[ y = ln \frac{N}{N_0} = \frac{A}{1 + e^{\frac{4\mu_m}{A} (\lambda - t) + 2}}\]

Here, \(N_0\) is the population size at \(t = 0\), \(A = ln \frac{N_\infty}{N_0}\) is the asymptote, \(\mu_m\) is the growth rate and \(\lambda\) the duration of the lag-phase.


Diffusion of attractants

The concentration of attractant molecules (\(c\)) in space changes according to a partial differential equation comprising diffusion, degradation and production by the prey bacteria.

\[ \frac{\partial c}{\partial t} = D\Delta c + p c_{prey} - a c\]


\(D\) is the diffusion coefficient, \(a\) is the degradation rate, \(p\) the rate of production and \(c_{prey}\) the concentration of prey/producer bacteria.

Chemotaxis

The chemotaxis of the hunter bacteria (BaKillus) is represented by an agent-based model adapted from [Matthäus ref]. Each bacterium has its own methylation and phosphorylation states of the chemotactic pathway which change according to a system of ordinary differential equations in response to attractant concentrations. In a classical 2-state model of bacterial chemotaxis, each bacterium will be in either running or tumbling state at each time point. In a running step, bacteria will swim forward in a straight line whereas in a tumbling step, they will change their direction by a random angle picked from a gamma distribution.

It should be noted that the model used here actually describes chemotaxis of E. coli. While the wiring of the chemotaxis pathway differs slightly, the same behavior is expected for B. subtilis . Therefore, we opted for the use of the better studied E. coli-model.

Implementation



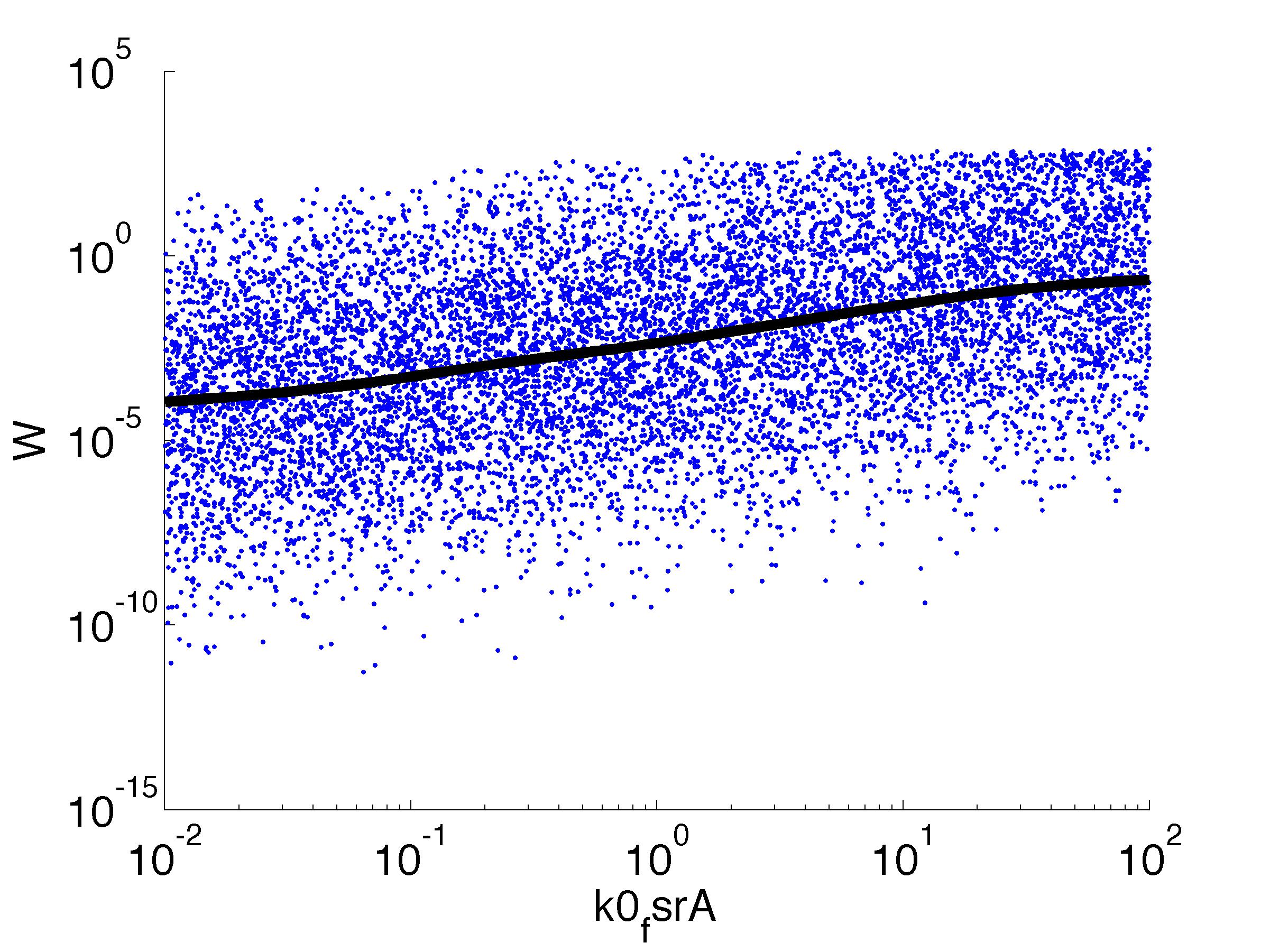
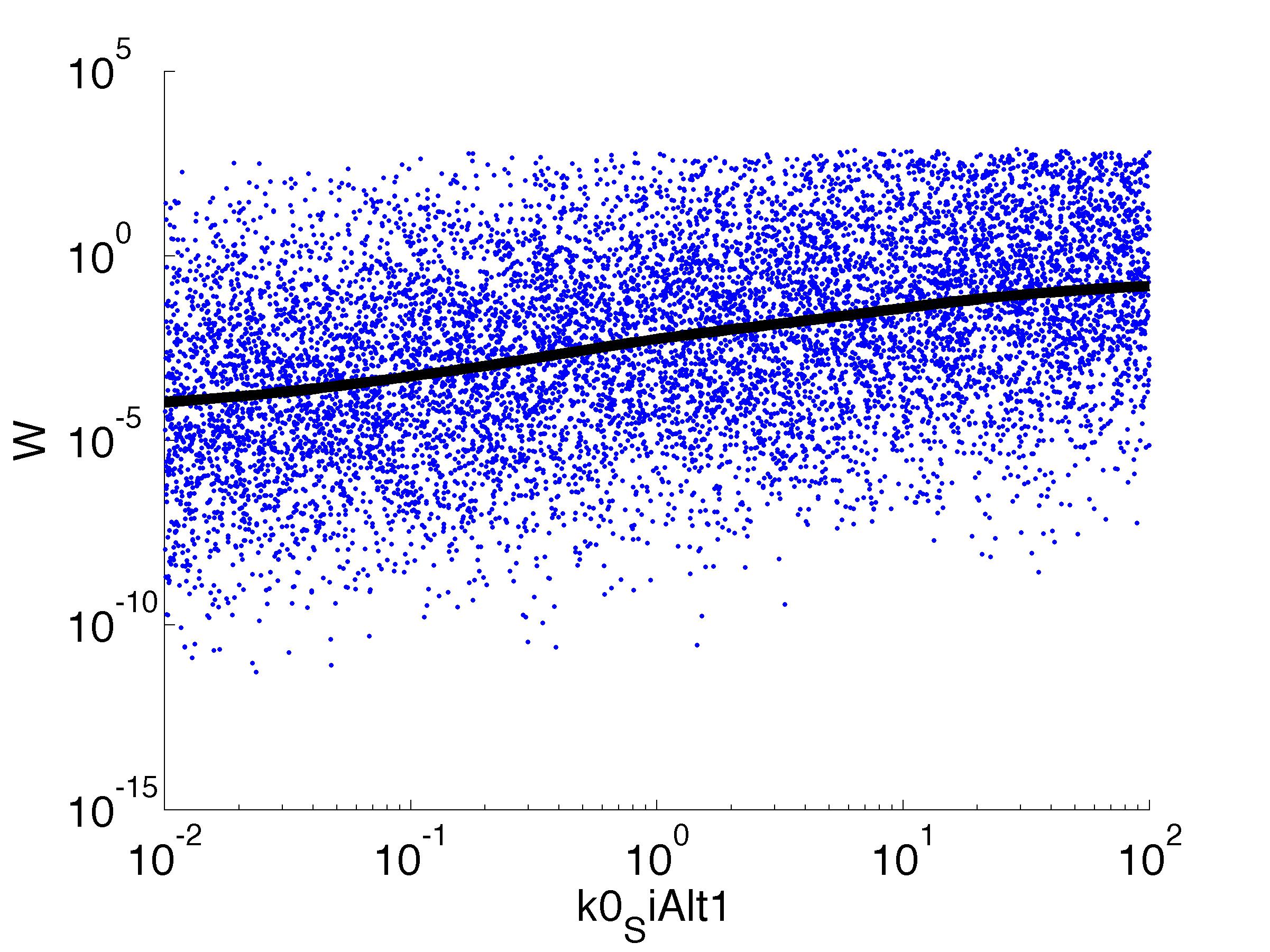
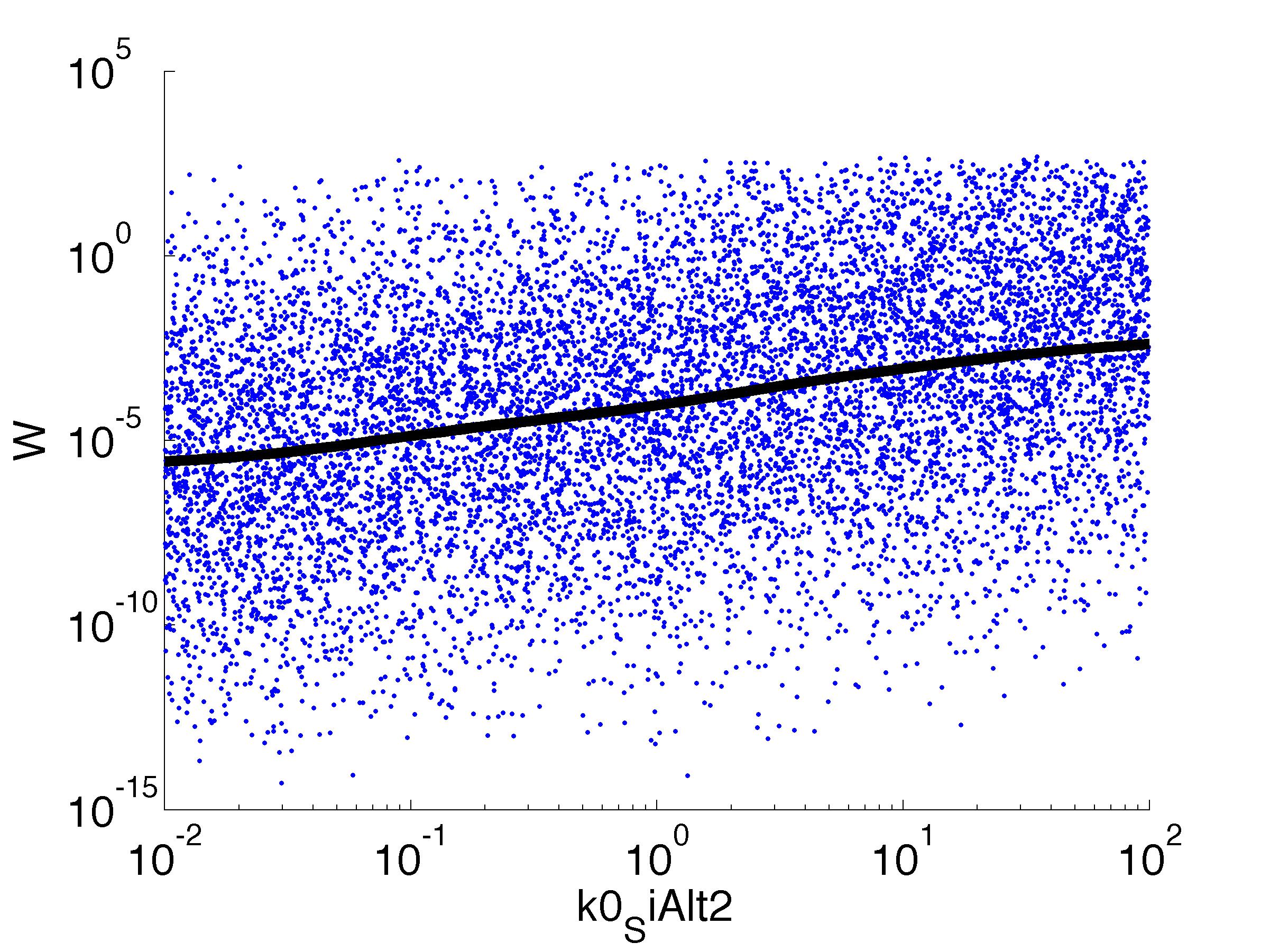
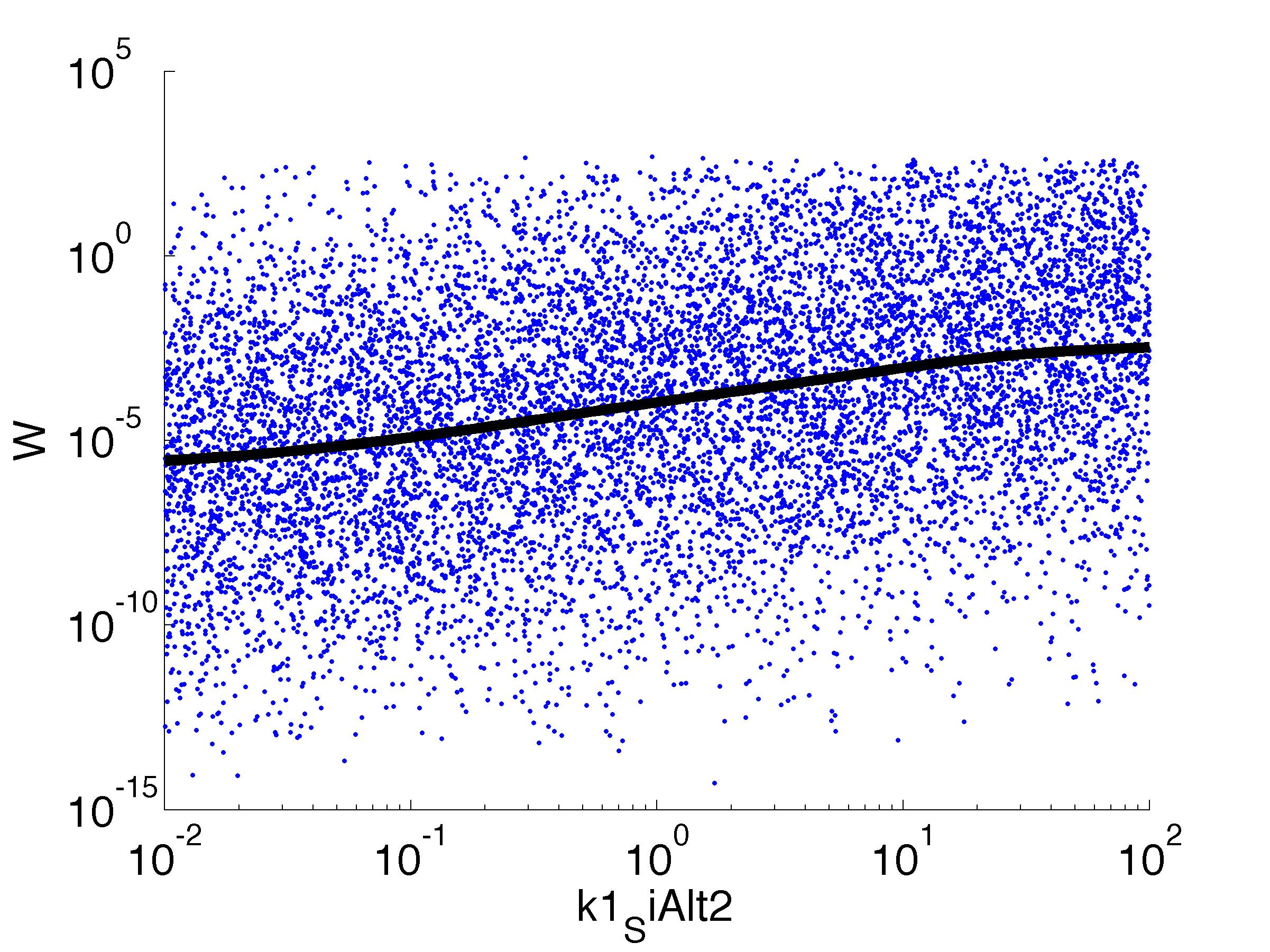
We implemented the model in C++, making extensive use of the Boost libraries for numerical integration, among other things. In addition, we wrote gateway routines to allow handling of the model from a MATLAB script. This way, parameters can easily be changed and results can be visualized using the plotting functionality of MATLAB.

Initially, the arena in which chemotaxis should take place is defined as a polygon. An equally spaced 2-dimensional grid covering the polygon is created to store concentrations of prey bacteria and attractant molecules (fig. x). The area in which prey bacteria grow (a 'colony') is defined as a rectangle and their initial concentration is set.

[scheme of grid]

A desired number of virtual hunter bacteria are created at set spacial coordinates. Initially, these bacteria have a random orientation and their chemotactic pathway is inactive (methylation and phosphorylation levels are zero).

The model is then updated by defined time steps until a desired end time is reached.


At each time step, the number of prey bacteria in the colony is updated according to their logistic growth curve. The concentration of attractant molecules changes according to the diffusion equation (see above). The Laplacian is discretized on the grid using a standard 5-point stencil (pseudocode??).

In each time step, the bacteria will update their chemotactic pathway (according to the system of differential equations) in response to the attractant concentration at their location (the mean of the nonnegative concentrations at the neighboring 4 grid nodes). Each bacterium will then swim forward (run) or change its orientation (tumble) dependent on the phosphorylation level of CheY.

Results & Discussion

Suicide Switch

For safety issues we want BaKillus to autoinduce apoptosis after successful completion of his task. This can be achieved by shutting down the production of resistance providing anti-toxin proteins. (see: Suicide-Switch) Still, BaKillus must produce sufficients amounts of toxins before inducing apotosis. Therefor, the negative feedback, which eventually stops production of anti-toxin must be sufficiently delayed to provide a sufficiently long timeframe for toxin production. However, as simple as this idea might sound in theory, robust practical implementation of such a module requires precise finetuning of the kinetics of the respective signalling cascade. In this model we tried to assess whether the inclusion of a secondary sigma factor could theoretically enhance the efficiency of the killing mechanism.

In the following we will compare two different models, one including only one sigma factor and one including two sigma factors. The models will be compared based on a fitness function which describes the difference between the toxin and antitoxin production over time. This should provide a measure of the effective number of produced toxin molecules.

Basic Model

The basic model only contains one sigma factor. The system of differential equations was derived following the standard paradigm of gene expression including mRNA aswell as protein dynamics. Inhibitory and Promoting activity were modeled via hill kinetics.

LMU14 Equations1.png


Variables

msdpABC:      Quantity of SdpABC mRNA
psdpABC: Quantity of SdpABC proteins
msdpI: Quantity of SdpI mRNA
psdpI: Quantity of SdpI proteins
mSiAlt1: Quantity of sigma factor mRNA
pSiAlt1: Quantity of sigma factor proteins
mfsrA: Quantity of FsrA mRNA
pfsrA: Quantity of FsrA proteins
Pqs: Quantity of QS proteins


Inquired Parameters

C0,Pqs: Basic concentration of QS proteins
C0,psdpI: Basic concentration of SdpI proteins
C0,fsrA: Basic concentration of FsrA proteins
k0,SiAlt1: Transcription Rate of sigma factor
k1,SiAlt1: Translation Rate of sigma factor
C0,SiAlt1:      Basic concentration of sigma factor proteins
k0,fsrA: Transcription Rate of FsrA
k1,fsrA: Translation Rate of FsrA


Fixed Parameters

In a first evaluation, the variation of following parameters were figured out to cause only insignificant variation of the model's fitness. Therefore they were keept at these specified values for all subsequent simulations:

Degradation rate (g1) of mRNA: 12 molecules per hour
Degradation rate (g2) of proteins: 1 molecule per hour
Transcription rate (k0) of Sdp: 7.2 per hour
Translation rate (k1) of SdpI & SdpABC:      10 per hour 


% par0 = lhsdesign(10000,12); 
par0 = rand(100000,12);
par = 10.^(4*par0 - 2); % Coveres range from 0.01 to 100

par(:,3) =12; % g1
par(:,5) =1; % g2
par(:,2) =0.12*60; % k0_sdp
par(:,4) =10; % k1_sdp

tout = linspace(0,10,100);
tic 
for j = 1:size(par,1)
   [~,~,x,y] = simulate_RRE_cannibalism(tout,par(j,:));
    %figure
    %plot(tout,y)
    %legend('p_{p_sdpABC}','p_{p_sdpI}')
   
   W(j) = sum(y(:,1)-y(:,2));
end
toc

parname={'C0_Pqs','k0_sdp','g1','k1_sdp','g2','C0_p_sdpI', ...
'C0_fsrA','k0_SiAlt1','k1_SiAlt1','C0_SiAlt1','k0_fsrA','k1_fsrA'};
 
for k = [1,6,7,8,9,10,11,12]
  figure
  scatter(par(:,k),W',10,'filled')
  hold on

  [xx,ind]=sort(par(:,k));
  r = ksr(log10(xx),W(ind));
 
  plot(10.^r.x,smooth(r.f,10),'k-','LineWidth',5)
  set(gca,'Yscale','lin')
  set(gca,'Xscale','log')
  xlabel(parname{k})
  ylabel('W')
  saveas(gcf,['parameter_' parname{k}]);
  print('-depsc2','-r300',['parameter_' parname{k}])
end


Fitness W

For analysis of the impact of each parameters, we used a function to determine the fitness W of the model. The fitness describes the integral of the surplus of toxic cannibalism proteins over the proprietary antidote. Therefore, a successful suicide equals a high fitness of the model. As we do not know the parameters in for our model we sampled the whole parameter space using a uniform sampler. Successively we used a Nadaraya-Watson kernel densiy estimator to approximate the expected value of W given a single parameter value. This allows us to asses the expected change in W when changing a single parameter, whithout knowledge of all other parameters.


LMU14 model 1.jpg
LMU14 model 2.jpg
LMU14 model 3.jpg
LMU14 model 4.jpg
LMU14 model 5.jpg
LMU14 model 6.jpg
LMU14 model 7.jpg
LMU14 model 8.jpg


As we can see..... some go up. some go down. one doesn't matter at all. we now know what parameter effect the system in what way.

Delayed Model

This model now considers a delayed SdpI inhibition which is realised by integrating a second sigma factor. The mathematical model for this system contains two additional equations for the new gene:


LMU14 Equations2.png


% par0 = lhsdesign(10000,12); 
par0 = rand(100000,15);
par = 10.^(4*par0 - 2); % Coveres range from 0.01 to 100

par(:,3) =12; % g1
par(:,5) =1; % g2
par(:,2) =0.12*60; % k0_sdp
par(:,4) =10; % k1_sdp

tout = linspace(0,10,1000);
tic 
for j = 1:size(par,1)
    [~,~,x,y] = simulate_RRE_cannibalism_twosigma(tout,par(j,:));
%      figure
%      plot(tout,y)
%      legend('p_{p_sdpABC}','p_{p_sdpI}')
%     
    W(j) = sum(y(:,1)-y(:,2));
end
toc

parname={'C0_Pqs','k0_sdp','g1','k1_sdp','g2','C0_p_sdpI','C0_fsrA', 'k0_SiAlt1', ...
 'k1_SiAlt1','k0_SiAlt2','k1_SiAlt2','C0_SiAlt2','C0_SiAlt1','k0_fsrA','k1_fsrA'};


for k = [1,6,7,8,9,10,11,12,13,14,15]
   figure
   scatter(par(:,k),W',10,'filled')
   hold on
 
   [xx,ind]=sort(par(:,k));
   r = ksr(log10(xx),W(ind));

   plot(10.^r.x,smooth(r.f,10),'k-','LineWidth',5)
   set(gca,'Yscale','lin')
   set(gca,'Xscale','log')
   xlabel(parname{k})
   ylabel('W')
   saveas(gcf,['red_parameter_' parname{k}]);
   print('-depsc2','-r300',['red_parameter_' parname{k}])
end


As above, the graphs show the statistical fitness W of the model plotted against each considered parameter. The black line resembles the average.


LMU14 model a.jpg
LMU14 model b.jpg
LMU14 model c.jpg
LMU14 model d.jpg
LMU14 model e.jpg
LMU14 model f.jpg
LMU14 model g.jpg
LMU14 model h.jpg
LMU14 model i.jpg
LMU14 model j.jpg
LMU14 model k.jpg


As we can see.....

Conclusion

Hi there!

Welcome to our Wiki! I'm BaKillus, the pathogen-hunting microbe, and I'll guide you on this tour through our project. If you want to learn more about a specific step, you can simply close the tour and come back to it anytime you like. So let's start!

What's the problem?

First of all, what am I doing here? The problem is, pathogenic bacteria all around the world are becoming more and more resistant against antimicrobial drugs. One major reason for the trend is the inappropriate use of drugs. With my BaKillus super powers, I want to reduce this misuse and thus do my part to save global health.

Sensing of pathogens

To combat the pathogenic bacteria, I simply eavesdrop on their communication. Bacteria talk with each other via quorum sensing systems, which I use to detect them and trigger my responses.

Adhesion

The more specific and effective I can use my powers, the lower the danger is of provoking new resistance development. So I catch pathogens whenever I get hold of them and stick to them until my work is done.

Killing

Talking about my work - killing pathogens is finally what I am made for. In response to quorum sensing molecules of the pathogens, I export a range of antimicrobial substances leading to dissipation of biofilms and the killing of the targeted bacteria.

Suicide switch

When the job is done and all the bad guys are finished, you don't need a super hero anymore. So after fulfilling my work I say goodbye to the world by activating my suicide switch.

Application

Of course I'm not only a fictional hero, but a very real one. In two different prototypes, I could be used for diagnosis or treatment of pathogen-caused diseases. However, there is still a whole lot of regulational and economical questions that have to be answered before.

See you!

So now you know my short story - and it is time for me to return to my fight for a safer world. Feel free to take a closer look on my super powers, the process of my development or the plans for a medical application.

Retrieved from "http://2014.igem.org/Team:LMU-Munich/Project/Modeling"