Team:Aachen/Notebook/Software/Measurarty
From 2014.igem.org
(→Segmentation) |
|||
| (42 intermediate revisions not shown) | |||
| Line 13: | Line 13: | ||
''Measurarty'' is the evil player in the game of ''Cellock Holmes'' and ''WatsOn''. | ''Measurarty'' is the evil player in the game of ''Cellock Holmes'' and ''WatsOn''. | ||
| - | Measurarty is the pathogen detection logic behind our project. | + | ''Measurarty'' is the pathogen detection logic behind our project. |
Using our ''Measurarty'' algorithm, we want to automatically detect pathogens from the chip photos delivered by WatsOn, without human interaction. | Using our ''Measurarty'' algorithm, we want to automatically detect pathogens from the chip photos delivered by WatsOn, without human interaction. | ||
Besides reducing the risk of human errors, this makes our device usable by almost everyone. | Besides reducing the risk of human errors, this makes our device usable by almost everyone. | ||
| Line 65: | Line 65: | ||
</center> | </center> | ||
</html> | </html> | ||
| + | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 75: | Line 76: | ||
Our [https://2014.igem.org/Team:Aachen/Notebook/Engineering/WatsOn#watsonsoftware device control software] is able to take images of incubated chips inside WatsOn. Yet, that does not bring the user closer to the answer of the question: | Our [https://2014.igem.org/Team:Aachen/Notebook/Engineering/WatsOn#watsonsoftware device control software] is able to take images of incubated chips inside WatsOn. Yet, that does not bring the user closer to the answer of the question: | ||
| - | <center> | + | <center>'''What's on the chip?'''</center> |
In fact, answering this question seems trivial for a human: Just check whether a colony grown has grown on the chip and you're done. This task is even easier with our chip system, because these show fluorescence wherever a pathogen has been detected. | In fact, answering this question seems trivial for a human: Just check whether a colony grown has grown on the chip and you're done. This task is even easier with our chip system, because these show fluorescence wherever a pathogen has been detected. | ||
| Line 84: | Line 85: | ||
First, ''Measurarty'' segments the target image using '''Statistical Region Merging (SRM)''' in order to find regions of similar properties. After this step, we can segment the picture using '''histogram thresholding''' in [http://en.wikipedia.org/wiki/HSL_and_HSV HSV color space] to find candidate regions for pathogens. | First, ''Measurarty'' segments the target image using '''Statistical Region Merging (SRM)''' in order to find regions of similar properties. After this step, we can segment the picture using '''histogram thresholding''' in [http://en.wikipedia.org/wiki/HSL_and_HSV HSV color space] to find candidate regions for pathogens. | ||
Finally, a classification algorithm can detect the pathogen on our chips. | Finally, a classification algorithm can detect the pathogen on our chips. | ||
| + | |||
| + | To demonstrate the algorithm, the following sample image will be discussed. | ||
| + | |||
| + | {{Team:Aachen/Figure|align=center|Aachen_meas_test.jpg|title=Image taken from WatsOn to be analyzed by ''Measurarty'' algorithm|width=700px}} | ||
| + | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 96: | Line 102: | ||
Compared to other clustering algorithms, SRM is quite leight weight, yet delivers ''deterministic'' results and is not dependent on a certain seed (like ''k''-means, for example). | Compared to other clustering algorithms, SRM is quite leight weight, yet delivers ''deterministic'' results and is not dependent on a certain seed (like ''k''-means, for example). | ||
| - | On the other hand, it can create as many refinements as one wants and is thus flexible enough for the our purposes. Finally there's already been knowledge about this algorithm in the group. | + | On the other hand, it can create as many refinements as one wants and is thus flexible enough for the our purposes. Finally, there's already been knowledge about this algorithm in the group. |
Statistical Region Merging (SRM) (Nook and Nielson, 2004) is a clustering technique also used directly for image segmentation. | Statistical Region Merging (SRM) (Nook and Nielson, 2004) is a clustering technique also used directly for image segmentation. | ||
| Line 104: | Line 110: | ||
Typically $Q$ is chosen as $Q \in \lbrack 256, 1\rbrack$ and $\delta = \frac{1}{\lvert I \rvert^2}$. | Typically $Q$ is chosen as $Q \in \lbrack 256, 1\rbrack$ and $\delta = \frac{1}{\lvert I \rvert^2}$. | ||
| - | The $Q$ parameter mainly influences the merging process. For an example, see the figure ''SRM Regions'' below. The lower the chosen value for $Q$, more coarse the regions become. Using a union-find structure, the segmentation does not need to be recalculated for each $Q$ level. For the step from $q$ to $\frac{q}{2}$, just the qualification criteria needs to be applied to the regions from the $q$ result. A MATLAB implementation is also available (Boltz, | + | The $Q$ parameter mainly influences the merging process. For an example, see the figure ''SRM Regions'' below. The lower the chosen value for $Q$, more coarse the regions become. Using a union-find structure, the segmentation does not need to be recalculated for each $Q$ level. For the step from $q$ to $\frac{q}{2}$, just the qualification criteria needs to be applied to the regions from the $q$ result. A MATLAB implementation is also available (Boltz, 2009). |
{{Team:Aachen/FigureDual|Aachen_srm_regions_3.PNG|Aachen_srm_regions_2.PNG|title1=SRM regions in random colors|title2=SRM regions (average color)|subtitle1=Different regions from an SRM run starting at $Q=256$ (top left) and going to $Q=1$ (bottom right). Each region is assigned a random color.|subtitle2=Different regions from an SRM run starting at $Q=256$ (top left) and going to $Q=1$ (bottom right). Each region is assigned the average color of that region.|width=425px}} | {{Team:Aachen/FigureDual|Aachen_srm_regions_3.PNG|Aachen_srm_regions_2.PNG|title1=SRM regions in random colors|title2=SRM regions (average color)|subtitle1=Different regions from an SRM run starting at $Q=256$ (top left) and going to $Q=1$ (bottom right). Each region is assigned a random color.|subtitle2=Different regions from an SRM run starting at $Q=256$ (top left) and going to $Q=1$ (bottom right). Each region is assigned the average color of that region.|width=425px}} | ||
| Line 113: | Line 119: | ||
For our purposes we only have one SRM run for $Q=256$. | For our purposes we only have one SRM run for $Q=256$. | ||
| - | In MATLAB, we use the previously mentioned code from MATLAB Fileexchange (Boltz, | + | In MATLAB, we use the previously mentioned code from MATLAB Fileexchange (Boltz, 2009). |
For our Qt-based GUI we implemented the SRM method ourselves. | For our Qt-based GUI we implemented the SRM method ourselves. | ||
| Line 126: | Line 132: | ||
</div> | </div> | ||
</html> | </html> | ||
| + | |||
| + | Finally, if applied to our test-image, regions are created and homogenoues regions form: | ||
| + | |||
| + | {{Team:Aachen/Figure|align=center|Aachen_meas_srmed.png|title=Regions created with SRM clustering|width=700px}} | ||
| + | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 186: | Line 197: | ||
</div> | </div> | ||
</html> | </html> | ||
| + | |||
| + | If you apply this HSV masking code to the SRMed test image, the following is created: | ||
| + | |||
| + | {{Team:Aachen/Figure|align=center|Aachen_meas_masked.png|title=Masked image|width=700px}} | ||
| + | |||
| + | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 193: | Line 210: | ||
<span class="anchor" id="classification"></span> | <span class="anchor" id="classification"></span> | ||
| - | == Automatic Classification == | + | === Smoothness Index === |
| + | |||
| + | For position prediction in virtual environments, jitter or noise in the output signal is not wanted though often present. | ||
| + | Since discovering smooth areas is a similar problem to jitter detection, a simple method for determining jitter can be used to measure non-jitter, smoothness (Joppich, Rausch and Kuhlen, 2013). | ||
| + | It is assumed that jitter-free areas of a position signal do not differ in velocity. | ||
| + | |||
| + | Smooth areas do not differ in intensity, and therefore only low changes in velocity (intensity change) can be recorded. | ||
| + | For the reduction of noise, this operation is performed on the smoothed input image. | ||
| + | Then the smoothness $s$ of a pixel $p$ in its k-neighbourhood $\mathcal{N}_k$ can be determined as: | ||
| + | \begin{equation} | ||
| + | s(p) = \sum\limits_{p' \in \mathcal{N}_k} \nabla(p') / \arg\max\limits_{p} s(p) | ||
| + | \end{equation} | ||
| + | |||
| + | Using thresholding, $TS_l \leq s(p) \leq TS_u \wedge TI_l \leq I \leq TI_u$, different areas, such as background or pathogen, can be selected. | ||
| + | |||
| + | For the empirical choice of thresholds, it can be argued that these are tailored to the specific case. | ||
| + | While this surely is true to a certain extent, the here presented method has been successfully tested on images from a completely different domain, and no changes to the thresholds have been made to make it work. | ||
| + | A proper theoretical evaluation is emphasized, however, is probably not the aim of the iGEM competition. | ||
| + | |||
| + | Finally, selecting for the red region, this delivers the location of possible pathogens. | ||
| + | Since the size of the agar chips is variable but fixed a quantitative analysis can be performed by counting pixels for instance. | ||
| + | |||
| + | === Empirical Evaluation === | ||
| + | |||
| + | Using our MATLAB code, we found the lower threshold for the smoothness index to be $TS_l = 0.85$ and the upper threshold $TS_u = \infty$. | ||
| + | Similarly, for $TI_l = 235$ and $TI_u = \infty$. | ||
| + | |||
| + | Using these settings, we can find a response already in images taken after 42 minutes. | ||
| + | |||
| + | Ideally, one would rate the quality of the image segmentation using some ground truth, such as manual delineations. This still has to be implemented for our method. | ||
| + | However, from visual observations, our method is showing promising results. | ||
| + | |||
| + | * image of smoothness index | ||
| + | |||
| + | === Automatic Classification === | ||
| Line 199: | Line 250: | ||
<div class="codediv"> | <div class="codediv"> | ||
<pre><code class="matlab"> | <pre><code class="matlab"> | ||
| - | function [mask seg] = automaticseeds( | + | function [mask, seg] = automaticseeds(im) |
| + | |||
| + | imc = im; | ||
| + | |||
| + | %% to grayscale and filtering | ||
| + | Z = double(rgb2gray(im)); | ||
| + | Z = 255 * Z / max(max(Z)); | ||
| + | |||
| + | filtertype = 'disk'; | ||
| + | Z = filter2(fspecial(filtertype), Z); | ||
| + | Z = filter2(fspecial(filtertype), filter2(fspecial(filtertype), Z)); | ||
| + | Z = 255 * Z / max(max(Z)); | ||
| + | |||
| + | %% calculating similarity score/smoothness index | ||
| + | k=4; | ||
| + | sSI = similarity(Z,k); | ||
| + | sSI = sSI / max(max(sSI)); | ||
| + | |||
| + | %% classify | ||
| + | pathogene = ((sSI > 0.85) == 1) & ((Z > 235) == 1); | ||
| + | |||
| + | mask = ones( size(imc) ); | ||
| + | seg = zeros( size(imc) ); | ||
| + | |||
| + | |||
| + | %% output | ||
| + | for i=1:size(im,1) | ||
| + | for j=1:size(im,2) | ||
| + | |||
| + | if (pathogene(i,j) == 1) | ||
| + | seg(i,j,1:3) = [255 0 0]; | ||
| + | mask(i, j, 1:3) = [0 0 0]; | ||
| + | end | ||
| + | end | ||
| + | end | ||
end | end | ||
</code></pre> | </code></pre> | ||
| Line 205: | Line 290: | ||
</html> | </html> | ||
| - | + | This code actually creates two intermediate images from which the similarity index is calculated. | |
| + | First the smoothed (disk-filter) input image is created and stored: | ||
| - | + | {{Team:Aachen/Figure|align=center|Aachen_meas_smoothed.png|title=Smoothed image|width=700px}} | |
| - | + | ||
| - | + | ||
| - | + | Only white regions are candidate regions. | |
| - | + | After smoothing, the similarity index is calculated. As expected, edges are detected and limit the area from which the target region can be selected. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | {{Team:Aachen/Figure|align=center|Aachen_meas_smiliarity.png|title=Smoothness Index|width=700px}} | |
| - | + | Finally the selected pathogen region is selected by the black area in the following picture: | |
| - | + | ||
| - | + | ||
| - | + | {{Team:Aachen/Figure|align=center|Aachen_meas_mask.png|title=Selected region|width=700px}} | |
| - | + | ||
| - | + | Combined with the input image, the final segmentation is received: | |
| - | == | + | {{Team:Aachen/Figure|align=center|Aachen_meas_final.png|title=Final the analyzed image|width=700px}} |
| - | + | [[File:Aachen_14-10-15_Medal_Cellocks_iNB.png|right|150px]] | |
| - | + | ||
| - | |||
| - | + | {{Team:Aachen/BlockSeparator}} | |
| - | + | ||
| + | == Achievements == | ||
| + | <span class="anchor" id="measurartyachievements"></span> | ||
| + | ''Measurarty'' is the image analysis logic behind our project. | ||
| + | It is comprised of simple constructs put together into a pipeline, that is clearly laid out, easily maintainable and - if needed - easily adaptable. | ||
| + | For example, changing from green to red fluorescence, only means to change the ''createMask'' function to select another target area. | ||
| - | + | Overall the results are convincing. We have not yet performed a comparison to a manual delineation, however, by eye the results look promising and have a low error. | |
| - | + | Talking about computational complexity, the MATLAB code of course performs better than our own C++ implementation, which must be regarded as a proof-of-principle. | |
| - | == | + | Space-wise, the code depends heavily on the image size $O( x \cdot y)$ (width $x$, height $y$, which also limits the number of edges in SRM between regions, as each pixel is one region to start with. However, it cannot take less memory, as the image is stored in an uncompressed format. |
| - | < | + | |
| + | On the computational side, the thresholding, image conversion and gradient steps are linear in the number of pixels, and are thus in $O(x \cdot y)$. | ||
| + | Unfortunately, the summation of the gradient for the smoothness index adds a heavy factor to it (k-neighbourhood for smoothness index). | ||
| + | Due to the merging step in our C++-SRM algorithm implementation, our code has to do $O(x^2 \cdot y^2)$ comparisons, which then finally results in a runtime complexity of $O( x^2 \cdot y^2)$. | ||
| + | |||
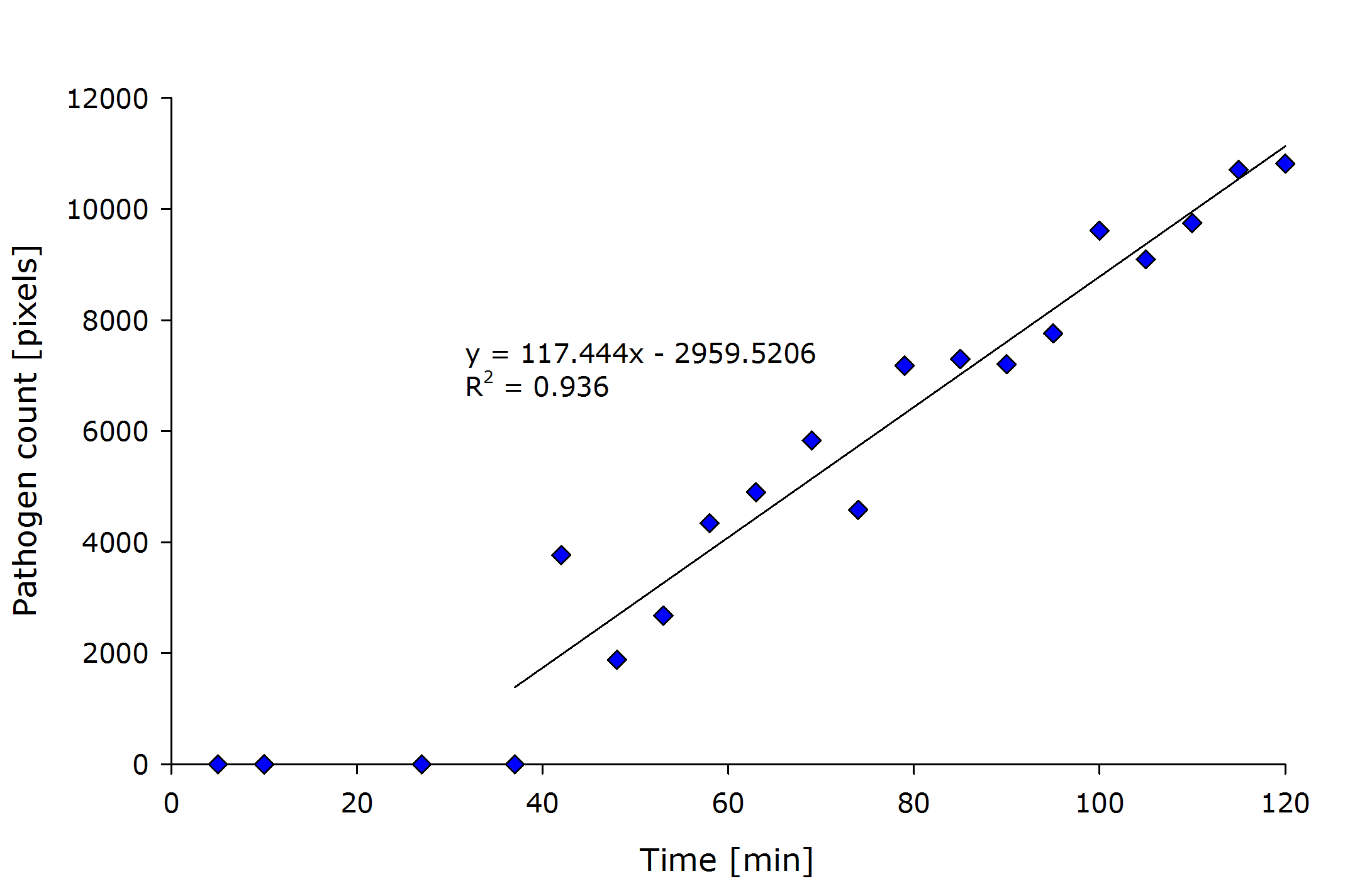
| + | {{Team:Aachen/Figure|align=center|Aachen_meas_sizes.png|title=Pixel count of the detected pathogenic region versus time after induction.|width=700px}} | ||
| + | |||
| + | From the above figure it can also be seen that the detected amount of pathogenic-area correlates with time after induction. | ||
| + | The lag-phase can be explained first by the lag-phase of the cells, which first need to generate a response to the pathogen, and on the other hand, by too low fluorescence which is not detectable. | ||
| + | The pixel count also meets the expectation when looking at the sample files by eye. | ||
| + | |||
| + | <center> | ||
| + | <div class="figure" style="float:{{{align|center}}}; margin: 0px 10px 10px 0px; border:{{{border|0px solid #aaa}}};width:{{{width|960px}}};padding:10px 10px 0px 0px;"> | ||
| + | {| | ||
| + | |<html> <img src="https://static.igem.org/mediawiki/2014/f/fc/Aachen_Measurarty_combined_slow.gif" width="960px"></html> | ||
| + | |- | ||
| + | |'''{{{title|Detecting ''P. aeroginosa'' with K131026}}}'''<br />{{{subtitle|The left half shows the original images from the device and the right half shows the same pictures with the detected pathogenic region analyzed by ''Measurarty''.}}} | ||
| + | |} | ||
| + | </div> | ||
| + | </center> | ||
| + | |||
| + | It can be concluded that the ''Measurarty'' pipeline defines a robustly working chip-analysis algorithm which can detect pathogens from images supplied by ''WatsOn''. | ||
| + | Therefore, this algorithm closes the gap between our biology, detection hardware and the user who wants easy-to-interpret results. | ||
| + | |||
| + | For future prospects, it would be interesting to do a proper performance analysis on our code, to find hotspots and optimize the code. Many ''for''-loops leave plenty of room for vectorization and loop-unrolling. Parallelization, specifically with respect to embedded hardware such as the Raspberry Pi or Odroid U3, is limited to the extend that the overhead created would probably eliminate the improvements. | ||
| - | |||
| - | |||
| - | |||
| - | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 258: | Line 357: | ||
<span class="anchor" id="source"></span> | <span class="anchor" id="source"></span> | ||
| - | * | + | ''Measuarty'' is the image analysis logic behind our project. It has been prototyped and developed in [http://www.mathworks.de/academia/student-competitions/igem/ MATLAB], and only later been ported into our ''WatsOn'' GUI. |
| - | * C++ | + | |
| - | + | We are happy to provide you with a zip-ped download of our MATLAB code here, as well as on the iGEM software repository on [https://github.com/orgs/igemsoftware/teams/aachen2014 github]. | |
| + | |||
| + | * [https://static.igem.org/mediawiki/2014/6/6e/Aachen_measurarty.zip MATLAB code] | ||
| + | * link [https://github.com/igemsoftware/AachenSoftProject2014/tree/master/measurarty github] | ||
| + | |||
| + | For the C++ conversion please see [https://2014.igem.org/Team:Aachen/Notebook/Engineering/WatsOn#watsonsoftware our ''WatsOn'' Software] section. | ||
| + | |||
| + | === Using the MATLAB Code === | ||
| + | |||
| + | In general, please follow the included ''README.MD'' file. Our package comes with a set of test files from one of our experiments. | ||
| + | After installing the Statistical Region Merging code (see readme), you can simply run ''igem_srm_demo.m''. Select your current folder, and MATLAB will automatically segment and classify the included jpg-images. | ||
| + | |||
{{Team:Aachen/BlockSeparator}} | {{Team:Aachen/BlockSeparator}} | ||
| Line 267: | Line 377: | ||
<span class="anchor" id="measurartyrefs"></span> | <span class="anchor" id="measurartyrefs"></span> | ||
| + | * Boltz, S. (2009, October 20). Image segmentation using statistical region merging - File Exchange - MATLAB Central. Image segmentation using statistical region merging. Retrieved December 12, 2013, from http://www.mathworks.com/matlabcentral/fileexchange/25619-image-segmentation-using-statistical-region-merging | ||
| + | |||
| + | * Joppich, M., Rausch, D., & Kuhlen, T. (2013). Adaptive human motion prediction using multiple model approaches.. Virtuelle und erweiterte Realität (p. 169–180). 10. Workshop der GI-Fachgruppe VR/AR: Shaker. | ||
| + | |||
| + | * Nock, R., & Nielsen, F. (2004). Statistical region merging. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26(11), 1452-1458. | ||
| - | |||
| - | |||
| - | |||
{{Team:Aachen/Footer}} | {{Team:Aachen/Footer}} | ||
Latest revision as of 03:46, 18 October 2014
|
|
|
|
|
|
|
 "
"