Team:ETH Zurich/modeling/whole
From 2014.igem.org
(→Dynamics) |
(→With Leakiness) |
||
| (55 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
<center> | <center> | ||
| - | {{:Team:ETH Zurich/tpl/scrollbutton|Model| | + | {{:Team:ETH Zurich/tpl/scrollbutton|Model|blue}} |
| - | {{:Team:ETH Zurich/tpl/scrollbutton2|Species| | + | {{:Team:ETH Zurich/tpl/scrollbutton2|Species|green}} |
{{:Team:ETH Zurich/tpl/scrollbutton3|Reactions|red}} | {{:Team:ETH Zurich/tpl/scrollbutton3|Reactions|red}} | ||
| - | {{:Team:ETH Zurich/tpl/ | + | {{:Team:ETH Zurich/tpl/scrollbutton|Equations|blue}} |
| - | {{:Team:ETH Zurich/tpl/ | + | {{:Team:ETH Zurich/tpl/scrollbutton2|Results|green}} |
| + | {{:Team:ETH Zurich/tpl/scrollbuttontworows|Alternate|Design|red}} | ||
</center> | </center> | ||
| Line 15: | Line 16: | ||
== Model == | == Model == | ||
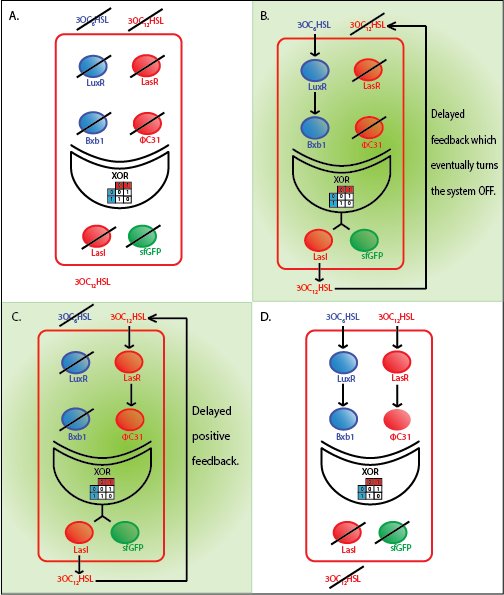
| - | The whole cell model is the combination of the Quorum sensing, Integrase and XOR modules. The model shows the behaviour of | + | The whole cell model is the combination of the Quorum sensing, Integrase and XOR modules. The model shows the behaviour of a single cell in response to incoming signals. The model enables us to understand the effect of leakiness, cross-talk and their combinations on the whole system. All the simulations here are described for a red cell .i.e. a cell producing LasI and GFP when it is ON. |
| - | [[File:ETHZ_WholeCellRedCell.png|800px|center|thumb|The four cases with different combinations of input for a red cell.]] | + | [[File:ETHZ_WholeCellRedCell.png|800px|center|thumb|'''Figure 1''' The four cases with different combinations of input for a red cell.]] |
<html></article></html> | <html></article></html> | ||
| Line 193: | Line 194: | ||
$$\begin{align*} | $$\begin{align*} | ||
| - | \frac{d[LuxAHL]}{dt} &= | + | \frac{d[LuxAHL]}{dt} &= -d_{LuxAHL}[LuxAHL]\\ |
\frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[LuxAHL][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ | \frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[LuxAHL][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ | ||
\frac{d[RLux]}{dt} &= k_{RLux}[LuxAHL][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ | \frac{d[RLux]}{dt} &= k_{RLux}[LuxAHL][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ | ||
| Line 203: | Line 204: | ||
\frac{d[SF_{Bxb1}]}{dt}&= 2 k_{ToffBxb1} [SA_{Bxb1}]^2 [T_{on,i}] + 2 k_{-Toff\phi C31} [SA_{Bxb1}]^2 [T_{off\phi C31}]\\ | \frac{d[SF_{Bxb1}]}{dt}&= 2 k_{ToffBxb1} [SA_{Bxb1}]^2 [T_{on,i}] + 2 k_{-Toff\phi C31} [SA_{Bxb1}]^2 [T_{off\phi C31}]\\ | ||
\\ | \\ | ||
| - | \frac{d[LasAHL]}{dt} &= | + | \frac{d[LasAHL]}{dt} &= -d_{LasAHL}[LasAHL] + DF * k_{LasAHL} [LasI]\\ |
\frac{d[LasR]}{dt} &= \alpha_{LasR} -k_{RLas}[LasAHL][LasR] + k_{-RLas}[RLas] - d_{LasR}[LasR] \\ | \frac{d[LasR]}{dt} &= \alpha_{LasR} -k_{RLas}[LasAHL][LasR] + k_{-RLas}[RLas] - d_{LasR}[LasR] \\ | ||
\frac{d[RLas]}{dt} &= k_{RLas}[LasAHL][LasR] - k_{-RLas}[RLas] - d_{RLas} [RLas] \\ | \frac{d[RLas]}{dt} &= k_{RLas}[LasAHL][LasR] - k_{-RLas}[RLas] - d_{RLas} [RLas] \\ | ||
| Line 236: | Line 237: | ||
=== Ideal case === | === Ideal case === | ||
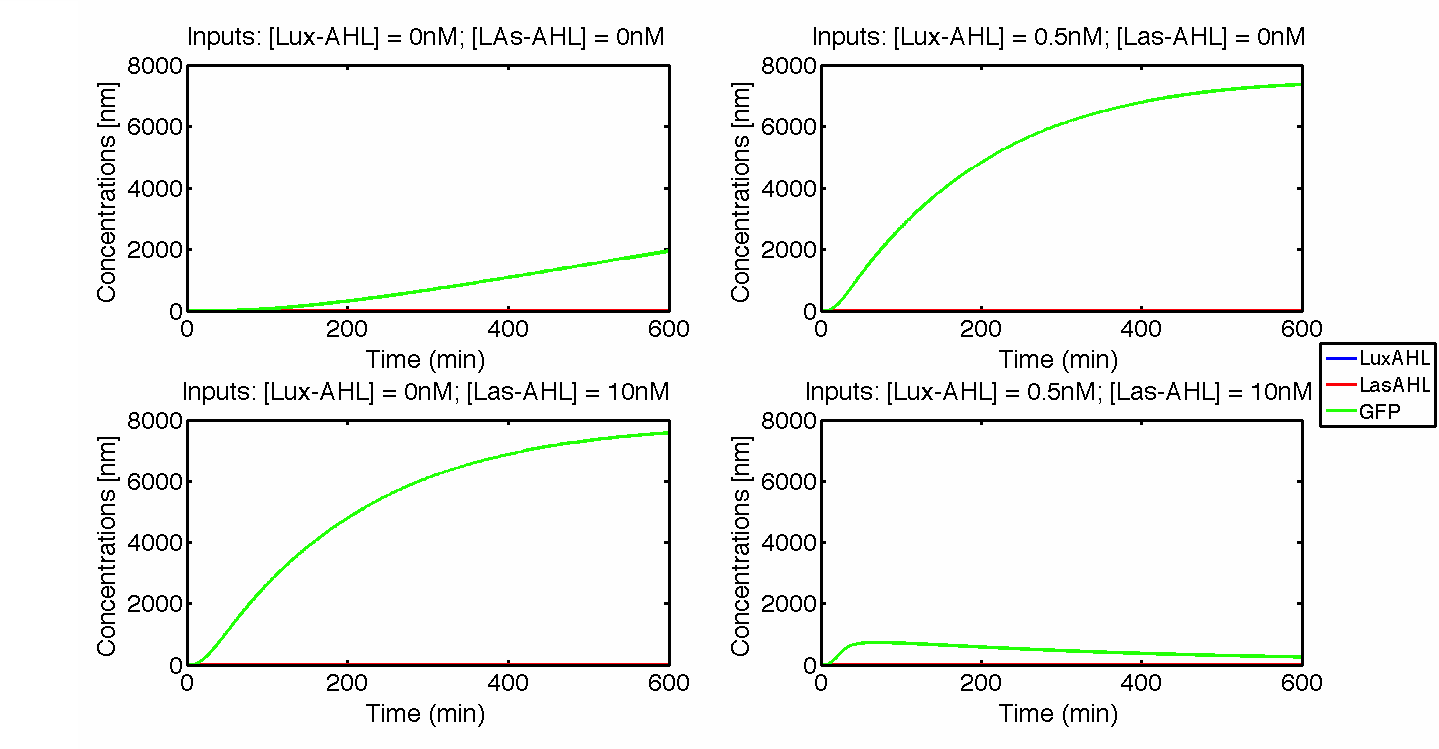
| - | [[File:ETHZ_IdealCase.png|center|800px|thumb|The four cases for the whole cell under ideal conditions]] | + | [[File:ETHZ_IdealCase.png|center|800px|thumb|'''Figure 2''' The four cases for the whole cell under ideal conditions. On [https://2014.igem.org/Team:ETH_Zurich/project/overview#Implementation_in_E._coli our project overview], you can see see in action how the circuit responds to different inputs.]] |
| - | Under ideal conditions, there is no leakiness or cross-talk. The | + | Under ideal conditions, there is no leakiness or cross-talk. The Figure 2 shows the production of GFP as a function of four different combinations of inputs in an ideal whole cell. No GFP is produced when there is no LasAHL and LuxAHL or when both are present. GFP is produced only when one of the input AHLs are present, thus emulating an XOR system. In the case with 0.5 nM of LuxAHL and no LasAHL as input, the rate of production of GFP reduces after six hours. This could be attributed to the delayed production of LasAHL from LasI. In the case with only LasAHL as input, there is a positive feedback of LasAHL. |
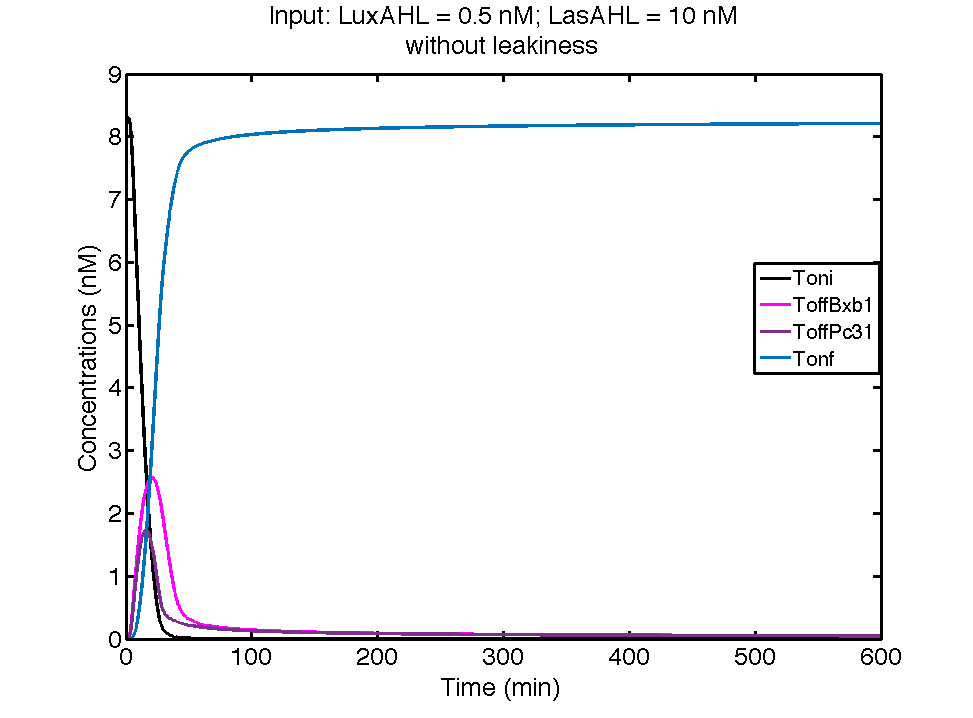
| - | [[File: | + | [[File:ETHZ_00TerminatorwithLeakiness.png|center|600px|thumb|'''Figure 3''' The dynamics of flipping of the terminators when the cell receives 0.5 nM LuxAHL and 0 nM of LasAHL and produces GFP and LasI]] |
| - | In the case above, the cell receives | + | In the case above, the cell receives 0.5 nM of LuxAHL and 10 nM LasAHL. This results in production of Bxb1 and ΦC31 respectively. Each terminator is flanked by binding sites for each of these integrases. These integrases flip the terminators by binding to their respective sites. Since, both integrases are present, the terminator is flipped twice thus eventually turning the system OFF. This is summarized in the figure above.Then, they flip the terminators again thus turning the system OFF. |
| + | At first the systems are ON either due to flipping by ΦC31 or Bxb1. This results in the production of LasI which catalyses the production of LasAHL. The LasAHL further increases the production of ΦC31 which flips the already flipped terminators by Bxb1. The remaining Bxb1 flips the already flipped terminators by ΦC31. Thus, the system eventually turns OFF.Even though there is more Bxb1 flipped terminators than those flipped by ΦC31. The dynamics of T<sub>oni</sub>, T<sub>offBxb1</sub>, T<sub>offΦC31</sub> and T<sub>onf</sub> is summarised in the figure above. | ||
| - | [[File:ETHZ_XORWholeCell.png|center|500px|thumb|Predicted XOR behaviour for the whole cell model without leakiness]] | + | |
| + | |||
| + | [[File:ETHZ_XORWholeCell.png|center|500px|thumb|'''Figure 4''' Predicted XOR behaviour for the whole cell model without leakiness]] | ||
| Line 257: | Line 261: | ||
| - | [[File:ETHZ_Leakiness.png|center|800px|thumb|The four cases for the whole cell with basal leakiness]] | + | [[File:ETHZ_Leakiness.png|center|800px|thumb|'''Figure 5''' The four cases for the whole cell with basal leakiness]] |
| - | From our experimental data, we observed some basal leakiness for P<sub>Lux</sub> and P<sub>Las</sub> even after using riboregulators. From the model we see that, this small basal leakiness is amplified downstream. The basal leakiness results in production of integrases which further act on the XOR module and cause the switching of the terminator. Thus, there is GFP and LasI produced, and the LasI produced further catalyses the production of more LasAHL. Thus, we observe some GFP even without inputs. | + | From our experimental data, we observed some basal leakiness for P<sub>Lux</sub> and P<sub>Las</sub> even after using riboregulators. From the model we see that, this small basal leakiness is amplified downstream. The basal leakiness results in production of integrases which further act on the XOR module and cause the switching of the terminator. Thus, there is GFP and LasI produced, and the LasI produced further catalyses the production of more LasAHL. Thus, we observe some GFP even without inputs. |
| - | <!--[[File:ETHZ_00TerminatorwithLeakiness.png|center|500px|thumb|No inputs and only basal leakiness]]--> | + | <!--[[File:ETHZ_00TerminatorwithLeakiness.png|center|500px|thumb|'''Figure 6''' No inputs and only basal leakiness]]--> |
| - | <!--The figure above | + | <!--The figure above summarizes the predicted effect of basal leakiness on the flipping of the terminator. The basal leakiness results in production of Bxb1 and ΦC31 which result in flipping of the terminator. In this case, since the cell produces LasI there is increased production of LasAHL. The LasAHL produced induces the production of ΦC31 which further causes flipping of all terminators flanked by the ΦC31 sites. Thus, by 200 minutes almost all ΦC31 sites are inactive and the cell will stay ON. --> |
| + | |||
| + | However, if we measure the fluorescence at around 400 mins, the effect of leakiness becomes negligible: in the case with null inputs, the level of the output concentration, GFP, is negligible compared to the level of the GFP concentration produced when the cell receives only one type of AHL. At this point, our model behaves like an XOR gate. Therefore, one of the solutions we propose is to kill or freeze the cells in each row after 6.5 hours. | ||
| - | |||
<!-- Alternatively, we propose a modified construct, where production of LasI is regulated by a weaker promoter and is induced by a protein, whose production is coupled with production of GFP. --> | <!-- Alternatively, we propose a modified construct, where production of LasI is regulated by a weaker promoter and is induced by a protein, whose production is coupled with production of GFP. --> | ||
| - | Initially from our model we observed that the feedback was rapid and hence, the amplification was much higher. However, from literature <sup>[[Team:ETH_Zurich/project/references|[9]]]</sup> we see that the XOR module is relatively slow. We were able to correct this by modelling transcription and translation steps. The delay introduced seems more | + | Initially from our model we observed that the feedback was rapid and hence, the amplification was much higher. However, from literature <sup>[[Team:ETH_Zurich/project/references|[9]]]</sup> we see that the XOR module is relatively slow. We were able to correct this by modelling transcription and translation steps. The delay introduced seems more realistic although we do not have our own experimental data to validate the same. Further, we use a dilution factor (DF) which represents the density of the cells in the bead. By choosing and appropriate DF we can get a more delayed response. |
| + | $$DF = \frac{No. of cells * V_{E.coli}}{V_{Bead}}$$ | ||
| - | |||
| - | + | [[File:ETHZ_XORWholeCellwithLeakiness.png|center|800px|thumb|'''Figure 6''' Predicted XOR behaviour for the whole cell model with leakiness]]. | |
| + | === With Leakiness and Crosstalk === | ||
| + | We modelled cross-talk by fitting Hill-functions to experimental data. For each quorum sensing module, there are two levels of [https://2014.igem.org/Team:ETH_Zurich/expresults cross-talk]. At the first level, we could have any of the two AHLs binding to a given regulator thus activating the promoter while at the second level there is cross talk between regulators and their respective native promoters. Thus, for activation of a given promoter, we can have four Hill functions corresponding to the combinations of inducer and regulator interactions. Since we are using two quorum sensing modules activating two different promoters, we have eight Hill functions. | ||
| + | As all the measurements were in terms of fluorescence, the V<sub>max</sub> for each Hill function was also in terms of fluorescence. In order to observe the effect of cross-talk we normalized the V<sub>max</sub> of non native interactions (in Lux system, P<sub>Lux</sub> being activated by LasAHL-LuxR, LasAHL-LasR or LuxAHL-LasR complexes) with the V<sub>max</sub> of the native interaction (LuxR binding to LuxAHL and activating P<sub>Lux</sub>). These ratios acted as weights for the effect of a non-native interaction on the promoter. | ||
| + | |||
| + | |||
| + | [[File:ETHZ_DynamicsWithCrossTalk.png|center|800px|thumb|'''Figure 7''' The four cases for the whole cell with basal leakiness and cross-talk]] | ||
| + | |||
| + | |||
| + | For an ideal whole cell model, it was necessary to have no or minimum leakiness and cross-talk. However, in reality this was not the case. Although we were able to reduce leakiness significantly using riboregulators, we still had the issue of cross-talk. However, we observe that the system acts as an XOR gate till about 300 mins even with cross talk. | ||
| + | In Figure 7 we observe the four cases with both cross-talk and leakiness. | ||
| + | |||
| + | |||
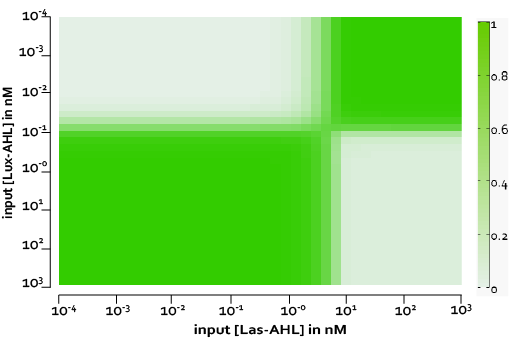
| + | [[File:ETHZ_WikiXORCTDiffLeakiness.png|center|500px|thumb|'''Figure 8''' The four cases for the whole cell with basal leakiness and cross-talk]] | ||
| + | |||
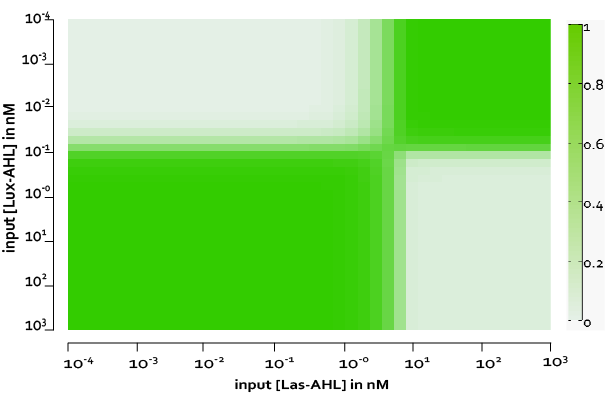
| + | Figure 8, shows the predicted XOR gate performance by a single cell model with basal leakiness and cross talk for different concentrations of LasAHL and LuxAHL at the end of 270 min. The system turns OFF when the input concentration of either AHLs is greater than 100 nM due to the effect of cross-talk. | ||
| + | |||
| + | |||
| + | <html></article></html> | ||
| + | <html><article id="Alternate"></html> | ||
| + | == Alternate Design == | ||
| + | We collaborated with the [https://2014.igem.org/Team:Edinburgh Edinburgh iGEM team 2014]. Their project is focused on communication between bacteria using metabolites as communicating molecules. Combining one metabolite molecule with another quorum sensing molecule could be a solution to avoid cross-talk. We derived a model on the molecular level of their problem (see the [https://2014.igem.org/Team:ETH_Zurich/modeling/qs#Alternate_Design Alternate Design section on the quorum sensing module page]). We inserted the equations in our system, putting B (metabolite) instead of LasAHL as communicating molecule. | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Here, we present the simulation results. The four possibilities of the XOR gate are presented in the following figure. The system was the one with a feedback corresponding to the metabolite pathway. Thus, when the only input is Lux-AHL, the cell will produce the metabolite B and create a feedback loop, which will switch off the gate. This behvior can indeed be observed on the following figure. | ||
| + | <br/> | ||
| + | <br/> | ||
| + | [[File:ETH_Zurich_Collaboration_Four_Cases.jpg|800px|center|thumb|'''Figure 9''' Dynamic simulations of the deterministic single-cell model. One input is a metabolite concentration. Cross-talk is then supposed to be assumed.]] | ||
| + | <br/> | ||
| + | <br/> | ||
| + | It exhibits an XOR behavior. It could be possible to combine quorum sensing and metabolite wiring to make the pattern appear. | ||
<html></article></html> | <html></article></html> | ||
{{:Team:ETH Zurich/tpl/foot}} | {{:Team:ETH Zurich/tpl/foot}} | ||
Latest revision as of 02:39, 18 October 2014
Whole cell model
Model
The whole cell model is the combination of the Quorum sensing, Integrase and XOR modules. The model shows the behaviour of a single cell in response to incoming signals. The model enables us to understand the effect of leakiness, cross-talk and their combinations on the whole system. All the simulations here are described for a red cell .i.e. a cell producing LasI and GFP when it is ON.
Chemical Species
| Name | Description |
|---|---|
| LuxAHL | 30C6-HSL is an acyl homoserine lactone which mainly binds to LuxR. |
| LuxR | Constitutively expressed regulator protein that can bind LuxAHL and stimulate transcription of Bxb1. |
| RLux | LuxR and LuxAHL complex which can dimerize. |
| DRLux | Dimerized form of RLux. |
| mRNABxb1 | mRNA of the Bxb1 integrase being transcribed by the Lux promoter. |
| Bxb1 | Serine integrase that can fold into two conformations - Bxb1a and Bxb1b. We chose to use a common connotation for both conformations - Bxb1. |
| DBxb1 | Dimerized form of Bxb1. We chose to use a common connotation for both homodimers, DBxb1a and DBxb1b. |
| LasAHL | 30C12-HSL is an acyl homoserine lactone which mainly binds to LasR. |
| LasR | Constitutively expressed regulator protein that can bind LasAHL and stimulate transcription of ΦC31. |
| RLas | LasR and LasAHL complex which can dimerize. |
| DRLas | Dimerized form of RLas. |
| mRNAΦC31 | mRNA of the ΦC31 integrase being transcribed by the Lux promoter. |
| ΦC31 | Serine integrase that can fold into two conformations - ΦC31a and ΦC31b. We chose to use a common connotation for both conformations - ΦC31. |
| DΦC31 | Dimerized form of ΦC31. We chose to use a common connotation for both homodimers, DΦC31a and DΦC31b. |
| SIBxb1 | Inactive DNA binding site for Bxb1. No dimer is bound to this site. |
| SABxb1 | Active DNA binding site for Bxb1. A dimer is bound to this site. |
| SFBxb1 | Flipped DNA binding site for Bxb1. The site generated after recombination by integrase. |
| SIΦC31 | Inactive DNA binding site for ΦC31. No dimer is bound to this site. |
| SAΦC31 | Active DNA binding site for ΦC31. A dimer is bound to this site. |
| SFΦC31 | Flipped DNA binding site for ΦC31. The site generated after recombination by integrase. |
| Ton,i | The number of terminators which are blocking the transcription of GFP and LuxI/LasI initially. |
| ToffBxb1 | The number of terminators turned off by recombination due to Bxb1. Favours the transcription of GFP and LuxI. |
| ToffΦC31 | The number of terminators turned off by recombination due to ΦC31. Favours the transcription of GFP and LuxI. |
| Ton,f | The number of terminators blocking the transcription of GFP and LuxI/LasI after recombination by Bxb1 and ΦC31. No transcription. |
| mRNAGFP | mRNA for Green fluorescent protein which is produced when the cells are ON. |
| GFP | Green fluorescent protein which is produced when the cells are ON. |
| mRNALuxI | mRNA for LuxI which is produced when the cells are ON. |
| LuxI | Enzyme catalysing the production of LuxAHL from SAM and ACP. |
| mRNALasI | mRNA for LasI which is produced when the cell are ON. |
| LasI | Enzyme catalysing the production of LasAHL from SAM and ACP. |
Reactions
$$ \begin{align} \emptyset&\rightarrow LuxR \\ LuxAHL+LuxR & \leftrightarrow RLux\\ RLux+RLux &\leftrightarrow DRLux\\ DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ P_{luxON}&\rightarrow P_{luxON}+mRNA_{Bxb1}\\ mRNA_{Bxb1}&\rightarrow Bxb1\\ Bxb1 + Bxb1 &\leftrightarrow DBxb1 \\ DBxb1 + SI_{Bxb1} & \leftrightarrow SA_{Bxb1}\\ LuxAHL &\rightarrow \emptyset\\ LuxR &\rightarrow \emptyset\\ RLux &\rightarrow \emptyset\\ DRLux &\rightarrow \emptyset\\ mRNA_{Bxb1} &\rightarrow \emptyset\\ Bxb1 &\rightarrow \emptyset\\ DBxb1 &\rightarrow \emptyset\\ \\ \emptyset&\rightarrow LasR \\ LasAHL+LasR & \leftrightarrow RLas \\ RLas+RLas & \leftrightarrow DRLas\\ DRLas+P_{LasOFF} & \leftrightarrow P_{LasON}\\ P_{LasON}&\rightarrow P_{LasON}+mRNA_{\phi C31}\\ mRNA_{\phi C31}&\rightarrow \phi C31\\ \phi C31 + \phi C31 &\leftrightarrow D\phi C 31 \\ D\phi C 31 + SI_{\phi C31} & \leftrightarrow SA_{\phi C31}\\ LasAHL &\rightarrow \emptyset\\ LasR &\rightarrow \emptyset\\ RLas &\rightarrow \emptyset\\ DRLas &\rightarrow \emptyset\\ mRNA_{\phi C31} &\rightarrow \emptyset\\ \phi C31 &\rightarrow \emptyset\\ D\phi C31 &\rightarrow \emptyset\\ \\ SA_{Bxb1}+SA_{Bxb1}+T_{on,i}& \rightarrow T_{offBxb1}+ SF_{Bxb1}+SF_{Bxb1}\\ T_{offBxb1} &\rightarrow T_{offBxb1} + mRNA_{GFP} + mRNA_{LasI} \\ SA_{\phi C31}+SA_{\phi C31}+T_{on,i}& \rightarrow T_{off\phi C31}+SF_{\phi C31}+SF_{\phi C31}\\ T_{off\phi C31} &\rightarrow T_{off\phi C31} + mRNA_{GFP} + mRNA_{LasI} \\ SA_{Bxb1}+SA_{Bxb1}+T_{off,\phi C31}& \rightarrow T_{on,f}+SF_{Bxb1}+SF_{Bxb1}\\ SA_{\phi C31}+SA_{\phi C31}+T_{offBxb1}& \rightarrow T_{on,f}+SF_{\phi C31}+SF_{\phi C31}\\ mRNA_{GFP} &\rightarrow GFP\\ mRNA_{LasI} &\rightarrow LasI\\ mRNA_{GFP} &\rightarrow \emptyset\\ mRNA_{LasI}&\rightarrow \emptyset\\ GFP &\rightarrow \emptyset\\ LasI&\rightarrow \emptyset\\ \\ S_{LasI}+LasI & \rightarrow LasAHL\\ \end{align}$$
Equations
The following equations were used for the whole cell model. The production of Bxb1 and ΦC31 is reduced to a hill function of RLux an RLas respectively. For details, check Quorum sensing module.
The equation is for a system which produces LasI and GFP as outputs. The LasI catalyses the production of LasAHL from SAM and ACP. Since, we do not know the amount of ACP or SAM present in the cell, we assume the rate of production of LasAHL to depend only on LasI concentration.
$$\begin{align*}
\frac{d[LuxAHL]}{dt} &= -d_{LuxAHL}[LuxAHL]\\
\frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[LuxAHL][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\
\frac{d[RLux]}{dt} &= k_{RLux}[LuxAHL][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\
\frac{d[mRNA_{Bxb1}]}{dt} &= L_{P_{Lux}} + \frac{K_{mRNA_{Bxb1}}[RLux]^2}{K_{mLux}^2 + [RLux]^2 }- d_{mRNA_{Bxb1}} [mRNA_{Bxb1}]\\
\frac{d[Bxb1]}{dt} &= k_{Bxb1} [mRNA_{Bxb1}] -2 k_{DBxb1}[Bxb1]^2+ 2 k_{-DBxb1}[DBxb1] - d_{Bxb1}[Bxb1]\\
\frac{d[DBxb1]}{dt}&= k_{DBxb1}[Bxb1]^2-k_{-DBxb1}[DBxb1]-k_{SABxb1}[DBxb1][SI_{Bxb1}]+k_{-SABxb1}[SA_{Bxb1}]-d_{DBxb1}[DBxb1]\\
\frac{d[SI_{Bxb1}]}{dt}&=-k_{SABxb1}[DBxb1][SI_{Bxb1}]+k_{-SABxb1}[SA_{Bxb1}]\\
\frac{d[SA_{Bxb1}]}{dt}&=k_{SABxb1}[DBxb1][SI_{Bxb1}]-k_{-SABxb1}[SA_{Bxb1}] - 2 k_{ToffBxb1} [SA_{Bxb1}]^2 [T_{on,i}] - 2 k_{-Toff\phi C31} [SA_{Bxb1}]^2 [T_{off\phi C31}]\\
\frac{d[SF_{Bxb1}]}{dt}&= 2 k_{ToffBxb1} [SA_{Bxb1}]^2 [T_{on,i}] + 2 k_{-Toff\phi C31} [SA_{Bxb1}]^2 [T_{off\phi C31}]\\
\\
\frac{d[LasAHL]}{dt} &= -d_{LasAHL}[LasAHL] + DF * k_{LasAHL} [LasI]\\
\frac{d[LasR]}{dt} &= \alpha_{LasR} -k_{RLas}[LasAHL][LasR] + k_{-RLas}[RLas] - d_{LasR}[LasR] \\
\frac{d[RLas]}{dt} &= k_{RLas}[LasAHL][LasR] - k_{-RLas}[RLas] - d_{RLas} [RLas] \\
\frac{d[mRNA_{\phi c31}]}{dt} &= L_{P_{Las}} + \frac{K_{mRNA_{\phi C31}}[RLas]^2}{K_{mLas}^2 + [RLas]^2 } - d_{mRNA_{\phi c31}} [mRNA_{\phi c31}]\\
\frac{d[\phi c31]}{dt} &= k_{\phi c31} [mRNA_{\phi c31}] -2 k_{D\phi c31}[\phi c31]^2+ 2 k_{-D\phi c31}[D\phi c31] - d_{\phi c31}[\phi c31]\\
\frac{d[D\phi c31]}{dt}&= k_{D\phi c31}[\phi c31]^2-k_{-D\phi c31}[D\phi c31]-k_{SA\phi c31}[D\phi c31][SI_{\phi c31}]+k_{-SA\phi c31}[SA_{\phi c31}]-d_{D\phi c31}[D\phi c31]\\
\frac{d[SI_{\phi c31}]}{dt}&=-k_{SA\phi c31}[D\phi c31][SI_{\phi c31}]+k_{-SA\phi c31}[SA_{\phi c31}]\\
\frac{d[SA_{\phi C31}]}{dt}&=k_{SA\phi C31}[D\phi C31][SI_{\phi C31}]-k_{-SA\phi C31}[SA_{\phi C31}] - 2 k_{Toff\phi C31} [SA_{\phi C31}]^2 [T_{on,i}] - 2 k_{-ToffBxb1} [SA_{\phi C31}]^2 [T_{offBxb1}]\\
\frac{d[SF_{\phi C31}]}{dt}&= 2 k_{Toff\phi C31} [SA_{\phi C31}]^2 [T_{on,i}] + 2 k_{-ToffBxb1} [SA_{\phi C31}]^2 [T_{offBxb1}]\\
\\
\frac{d[T_{on,i}]}{dt}&= -k_{ToffBxb1}[T_{on,i}][SA_{Bxb1}]^2 -k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 \\
\frac{d[T_{offBxb1}]}{dt}&=k_{ToffBxb1} [T_{on,i}][SA_{Bxb1}]^2 - k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2\\
\frac{d[T_{off\phi C31}]}{dt}&=k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 - k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\
\frac{d[T_{on,f}]}{dt}&= k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2 + k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\
\\
\frac{d[mRNA_{LasI}]}{dt}&= k_{mRNA_{LasI}} (\frac{[T_{offBxb1}]}{\theta + [T_{offBxb1}]} + \frac{[T_{off\phi C31}]}{\theta + [T_{off\phi C31}]}) - d_{mRNA_{LasI}}[mRNA_{LasI}]\\
\frac{d[LasI]}{dt}&= k_{LasI} [mRNA_{LasI}] - d_{LasI}[LasI]\\
\frac{d[mRNA_{GFP}]}{dt}&= k_{mRNA_{GFP}} (\frac{[T_{offBxb1}]}{\theta + [T_{offBxb1}]} + \frac{[T_{off\phi C31}]}{\theta + [T_{off\phi C31}]}) - d_{mRNA_{GFP}}[mRNA_{GFP}]\\
\frac{d[GFP]}{dt}&= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP]\\
\end{align*}$$
Dynamics
Ideal case

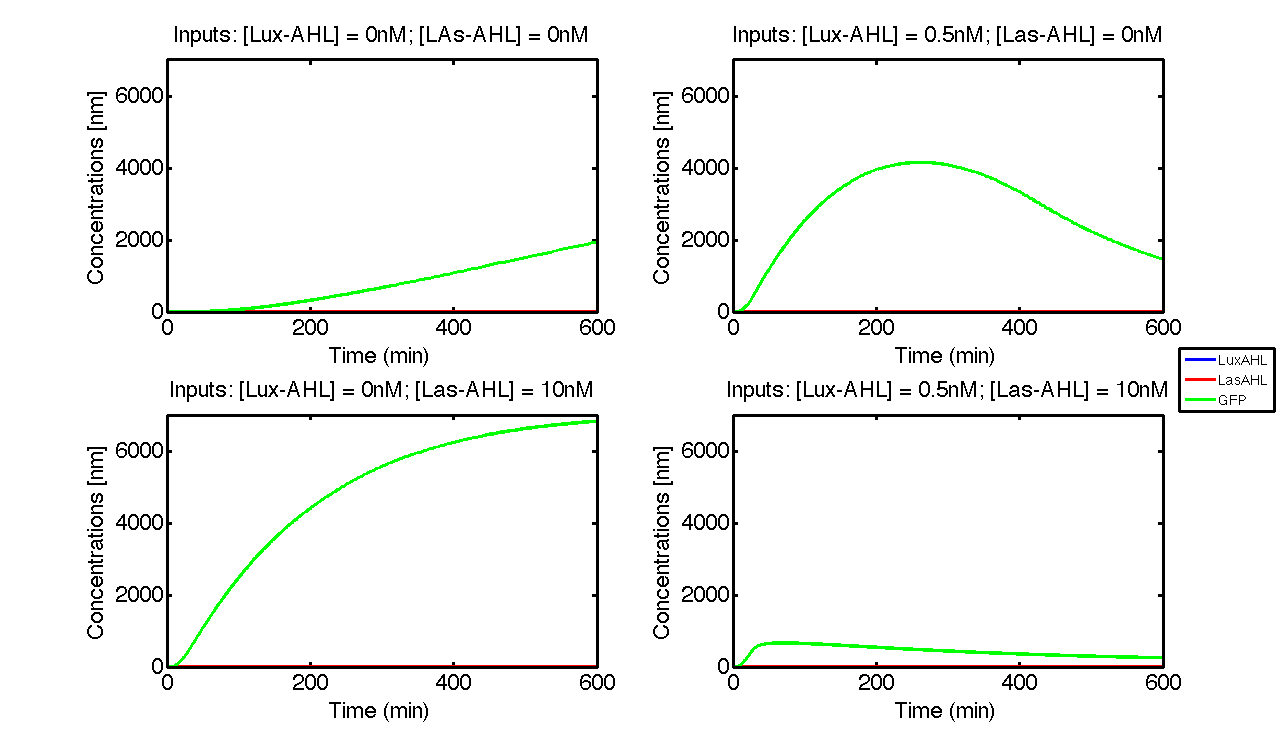
Under ideal conditions, there is no leakiness or cross-talk. The Figure 2 shows the production of GFP as a function of four different combinations of inputs in an ideal whole cell. No GFP is produced when there is no LasAHL and LuxAHL or when both are present. GFP is produced only when one of the input AHLs are present, thus emulating an XOR system. In the case with 0.5 nM of LuxAHL and no LasAHL as input, the rate of production of GFP reduces after six hours. This could be attributed to the delayed production of LasAHL from LasI. In the case with only LasAHL as input, there is a positive feedback of LasAHL.
In the case above, the cell receives 0.5 nM of LuxAHL and 10 nM LasAHL. This results in production of Bxb1 and ΦC31 respectively. Each terminator is flanked by binding sites for each of these integrases. These integrases flip the terminators by binding to their respective sites. Since, both integrases are present, the terminator is flipped twice thus eventually turning the system OFF. This is summarized in the figure above.Then, they flip the terminators again thus turning the system OFF.
At first the systems are ON either due to flipping by ΦC31 or Bxb1. This results in the production of LasI which catalyses the production of LasAHL. The LasAHL further increases the production of ΦC31 which flips the already flipped terminators by Bxb1. The remaining Bxb1 flips the already flipped terminators by ΦC31. Thus, the system eventually turns OFF.Even though there is more Bxb1 flipped terminators than those flipped by ΦC31. The dynamics of Toni, ToffBxb1, ToffΦC31 and Tonf is summarised in the figure above.
The figure above, shows the predicted XOR gate performance by a single cell model with no basal leakiness for different concentrations of LasAHL and LuxAHL.
With Leakiness
From our experimental data, we observed some basal leakiness for PLux and PLas even after using riboregulators. From the model we see that, this small basal leakiness is amplified downstream. The basal leakiness results in production of integrases which further act on the XOR module and cause the switching of the terminator. Thus, there is GFP and LasI produced, and the LasI produced further catalyses the production of more LasAHL. Thus, we observe some GFP even without inputs.
However, if we measure the fluorescence at around 400 mins, the effect of leakiness becomes negligible: in the case with null inputs, the level of the output concentration, GFP, is negligible compared to the level of the GFP concentration produced when the cell receives only one type of AHL. At this point, our model behaves like an XOR gate. Therefore, one of the solutions we propose is to kill or freeze the cells in each row after 6.5 hours.
Initially from our model we observed that the feedback was rapid and hence, the amplification was much higher. However, from literature [9] we see that the XOR module is relatively slow. We were able to correct this by modelling transcription and translation steps. The delay introduced seems more realistic although we do not have our own experimental data to validate the same. Further, we use a dilution factor (DF) which represents the density of the cells in the bead. By choosing and appropriate DF we can get a more delayed response.
$$DF = \frac{No. of cells * V_{E.coli}}{V_{Bead}}$$
With Leakiness and Crosstalk
We modelled cross-talk by fitting Hill-functions to experimental data. For each quorum sensing module, there are two levels of cross-talk. At the first level, we could have any of the two AHLs binding to a given regulator thus activating the promoter while at the second level there is cross talk between regulators and their respective native promoters. Thus, for activation of a given promoter, we can have four Hill functions corresponding to the combinations of inducer and regulator interactions. Since we are using two quorum sensing modules activating two different promoters, we have eight Hill functions.
As all the measurements were in terms of fluorescence, the Vmax for each Hill function was also in terms of fluorescence. In order to observe the effect of cross-talk we normalized the Vmax of non native interactions (in Lux system, PLux being activated by LasAHL-LuxR, LasAHL-LasR or LuxAHL-LasR complexes) with the Vmax of the native interaction (LuxR binding to LuxAHL and activating PLux). These ratios acted as weights for the effect of a non-native interaction on the promoter.
For an ideal whole cell model, it was necessary to have no or minimum leakiness and cross-talk. However, in reality this was not the case. Although we were able to reduce leakiness significantly using riboregulators, we still had the issue of cross-talk. However, we observe that the system acts as an XOR gate till about 300 mins even with cross talk.
In Figure 7 we observe the four cases with both cross-talk and leakiness.
Figure 8, shows the predicted XOR gate performance by a single cell model with basal leakiness and cross talk for different concentrations of LasAHL and LuxAHL at the end of 270 min. The system turns OFF when the input concentration of either AHLs is greater than 100 nM due to the effect of cross-talk.
Alternate Design
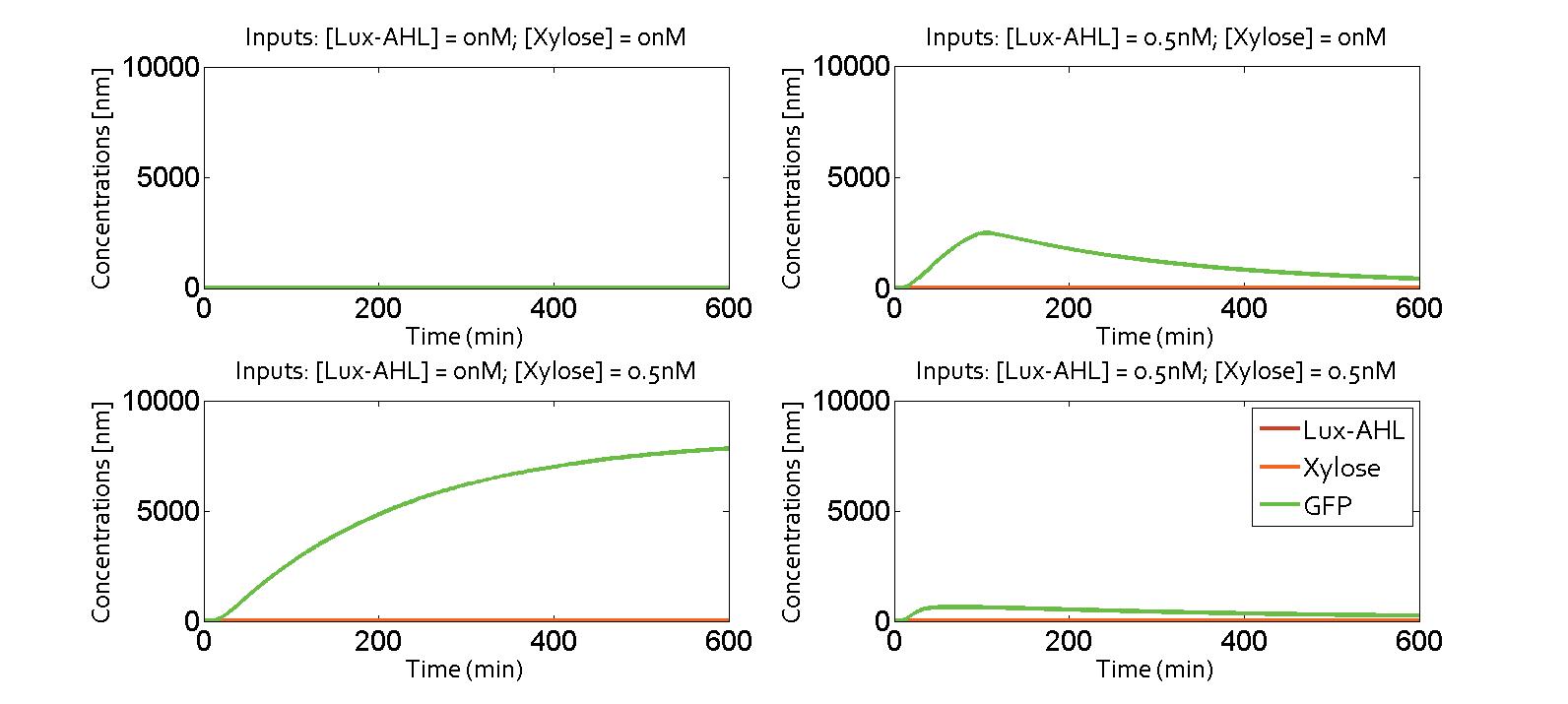
We collaborated with the Edinburgh iGEM team 2014. Their project is focused on communication between bacteria using metabolites as communicating molecules. Combining one metabolite molecule with another quorum sensing molecule could be a solution to avoid cross-talk. We derived a model on the molecular level of their problem (see the Alternate Design section on the quorum sensing module page). We inserted the equations in our system, putting B (metabolite) instead of LasAHL as communicating molecule.
Here, we present the simulation results. The four possibilities of the XOR gate are presented in the following figure. The system was the one with a feedback corresponding to the metabolite pathway. Thus, when the only input is Lux-AHL, the cell will produce the metabolite B and create a feedback loop, which will switch off the gate. This behvior can indeed be observed on the following figure.
It exhibits an XOR behavior. It could be possible to combine quorum sensing and metabolite wiring to make the pattern appear.
 "
"