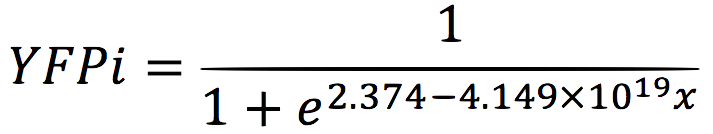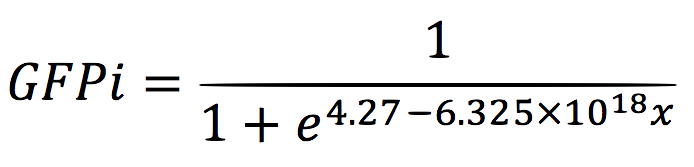Team:BIOSINT Mexico/Results
From 2014.igem.org
| (40 intermediate revisions not shown) | |||
| Line 19: | Line 19: | ||
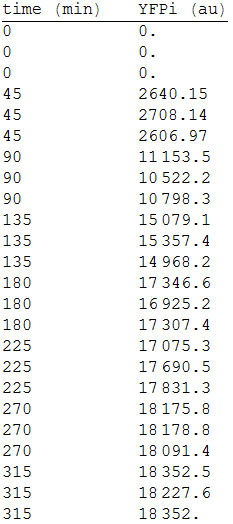
:::[[File:1res.png|150px|thumb|left|'''Figure 1''' YFP intensity every 45 minutes.]] | :::[[File:1res.png|150px|thumb|left|'''Figure 1''' YFP intensity every 45 minutes.]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
We made three repetitions, so in order to model the equation, we obtained the mean measure, therefore: | We made three repetitions, so in order to model the equation, we obtained the mean measure, therefore: | ||
| Line 24: | Line 49: | ||
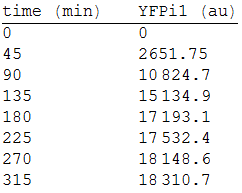
| - | :[[File:2res.png|300px|thumb| | + | ::::::[[File:2res.png|300px|thumb|left|'''Figure 2''' Media YFP intensity every 45 minutes.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
We analysed the data and using the Wolfram Mathematica software, we obtained the following equation that fits the data. | We analysed the data and using the Wolfram Mathematica software, we obtained the following equation that fits the data. | ||
If we plot this equation, we obtain: | If we plot this equation, we obtain: | ||
| - | [[File:Model1res.png|400px|center]] | + | [[File:Model1res.png|400px|center|]] |
Where we can see that the intensity of YFP grows directly proportional to the time and concentration of the molecule. | Where we can see that the intensity of YFP grows directly proportional to the time and concentration of the molecule. | ||
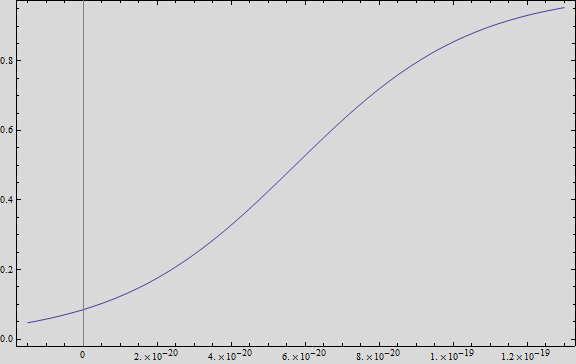
| - | [[File:4res.png|600px|center]] | + | ::::::[[File:4res.png|600px|left|center|'''Figure 3''' Intensity YFP vs time.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<h2>Mer Operon Expression</h2> | <h2>Mer Operon Expression</h2> | ||
| Line 39: | Line 97: | ||
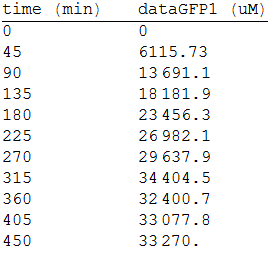
First, we measured the GFP fluorescense intensity every 45 minutes. | First, we measured the GFP fluorescense intensity every 45 minutes. | ||
| - | [[File:5res.png|400px| | + | ::::::[[File:5res.png|400px|left|thumb|'''Figure 4''' GFP fluorescense intensity every 45 minutes.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
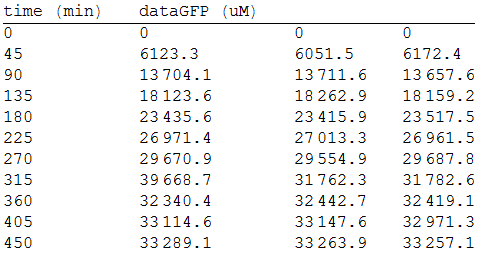
As we make three repetitions, we take the mean values as input data for the regression. The analized data was: | As we make three repetitions, we take the mean values as input data for the regression. The analized data was: | ||
| - | [[File:6res.png|400px| | + | ::::::[[File:6res.png|400px|left|thumb|'''Figure 5''' GFP fluorescense media intensity every 45 minutes.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
For the regression, we used the Wolfram Mathematica software and obtained the equation: | For the regression, we used the Wolfram Mathematica software and obtained the equation: | ||
| Line 51: | Line 146: | ||
Thus, if we plot the equation we obtain that: | Thus, if we plot the equation we obtain that: | ||
| - | [[File:Meperdi.png|400px| | + | |
| + | :::::::[[File:Meperdi.png|400px|left|thumb|'''Figure 6''' Graphic GFP fluorescense media intensity vs time.]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
And, as we see in the graph, GFP expresses directly proportional to time, given the strenght of the promoter upstream. | And, as we see in the graph, GFP expresses directly proportional to time, given the strenght of the promoter upstream. | ||
| Line 57: | Line 171: | ||
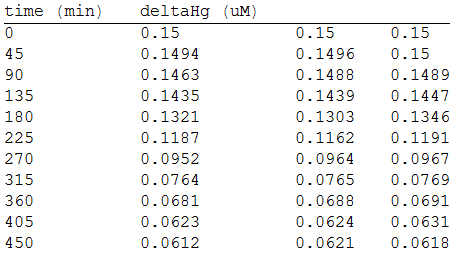
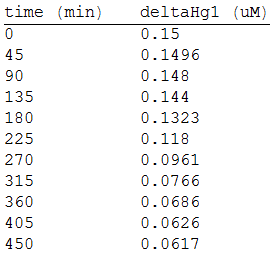
The change in the concentration of methyl mercury was also measured. We choose to measure it instead of the mercury accumulated inside the cells because it was easier. The collected data is provided in the table: | The change in the concentration of methyl mercury was also measured. We choose to measure it instead of the mercury accumulated inside the cells because it was easier. The collected data is provided in the table: | ||
| - | [[File:Ul1.png|400px| | + | |
| + | |||
| + | |||
| + | |||
| + | :::::::[[File:Ul1.png|400px|left|thumb|'''Figure 7''' Concentration of methyl mercury inside cell every 45 minutes.]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
As in the other experiments, we analyzed the mean values of the concentration in order to make the regression: | As in the other experiments, we analyzed the mean values of the concentration in order to make the regression: | ||
| - | [[File:Ul2.png|400px| | + | :::::::[[File:Ul2.png|400px|left|thumb|'''Figure 8''' Media concentration of methyl mercury inside cell every 45 minutes.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Obtaining the polynomial equation: | Obtaining the polynomial equation: | ||
| Line 69: | Line 225: | ||
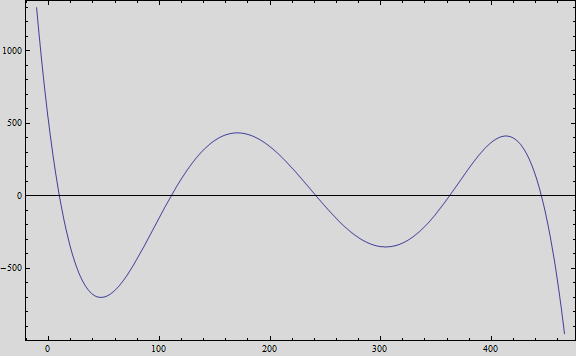
And, if we plot the equation we obtain the following graph: | And, if we plot the equation we obtain the following graph: | ||
| - | [[File:Ul3.png|400px| | + | :::::::[[File:Ul3.png|400px|left|thumb|'''Figure 9''' Graphic of concentration methyl mercury inside cell.]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
That, at short term, fits the behavior of the expected values. | That, at short term, fits the behavior of the expected values. | ||
Latest revision as of 04:00, 18 October 2014
Results
Red Light Switch
We fused the promoter PCMV (BBa_K747096) to a YFP reporter (BBa_E0030).
In order to measure its expression, we culture transformed E.coli in agar plates and measured the fluorescense intensity every 45 minutes. After that, we obtained the following data. [Fig.1]
We made three repetitions, so in order to model the equation, we obtained the mean measure, therefore:
We analysed the data and using the Wolfram Mathematica software, we obtained the following equation that fits the data.
If we plot this equation, we obtain:
Where we can see that the intensity of YFP grows directly proportional to the time and concentration of the molecule.
Mer Operon Expression
In order to measure the mer operon expression fused the composite to a GFP reporter and analized the bioremediation by measuring the change of the concentration of methyl mercury in the media. First, we measured the GFP fluorescense intensity every 45 minutes.
As we make three repetitions, we take the mean values as input data for the regression. The analized data was:
For the regression, we used the Wolfram Mathematica software and obtained the equation:
Thus, if we plot the equation we obtain that:
And, as we see in the graph, GFP expresses directly proportional to time, given the strenght of the promoter upstream. Then, as GFP expresses at aproximately the same rate that the mer operon proteins, it is posible to infer that the GFP concentration given any time is the same as the mer operon proteins concentration attached upstream. The change in the concentration of methyl mercury was also measured. We choose to measure it instead of the mercury accumulated inside the cells because it was easier. The collected data is provided in the table:
As in the other experiments, we analyzed the mean values of the concentration in order to make the regression:
Obtaining the polynomial equation:
And, if we plot the equation we obtain the following graph:
That, at short term, fits the behavior of the expected values.
 "
"