For the bioremediation aspect of DCMation, we managed to achieve the following:
dcmA-sfGFP is expressed in E. coli
 Figure 1
Figure 1
(A)A western blot showing the expression of a protein at 62 kDa (the calculated molecular weight of DCMA-sfGFP). The existence of some protein product at 0 mM IPTG suggests that the promoter is slightly ‘leaky’ and allows a basal expression level when no inducer is present.
(B) The image shows the expression of GFP under blue LED light in E. coli at various concentrations of the inducer IPTG. The graph quantifies the observed fluorescence, correcting for differences in optical density at 600 nm. Expression significantly increases with IPTG concentration as expected well above the basal level at 0 mM IPTG
Successful expression of microcompartments in E.coli
We successfully expressed the pdu-ABTUNJK microcompartment in E.coli, as indicated in the Western-blot of subunits B, U, N and K in the figure below:
 Figure 2
Figure 2
This figure shows the a western blot using anti-his tag antibodies. Subunits B, U, N and K have a C-terminal his-tag each.
Proteins can be targeted to microcompartments
Proteins can be inserted into the microcompartment when they have an N-terminal targeting sequence.
In order to show that this targeting mechanism works for our constructs, we have constructed a plasmid with sfGFP fused to the N-terminal tag. When transforming this vector into E.coli along with the pUNI-ABTUNJK vector, we observed high-density fluorescence spots in those cells that expressed both the microcompartment and microcompartment-tagged sfGFP. This is shown in the image on the left, whereas the image on the right shows a control sample without the pUNI-ABTUNJK vector, thus expressing sfGFP evenly in the cell.

 Figure 3 A and B
Figure 3 A and B
(Figure 3 A- Left) Fluorescence image of E.coli transformed with vectors containing microcompartment tagged sfGFP and the microcompartment
(Figure 3 B - Right) Fluorescence image of E.coli transformed with a vector (pOxon1) containing microcompartment-tagged sfGFP only
In order to further our understanding of the systems we are dealing with, we developed the following simulations:
1. Microcompartment Shape Model: (see
'Predicting the microcompartment structure') a model that simulates the effect of random point deviations in the microcompartment structure from the perfect icosahedral structure seen in carboxysomes.
 Figure 4
Figure 4
The output of the microcompartment shape model is a simulated microcompartment structure (blue) plotted alongside the perfect icosahedral structure of a carboxysome (red) which we used as a starting point for predicting the geometric structure of a microcompartment.
2. Prediction of number of enzymes per microcompartment: (see
'Modelling the number of enzymes in a microcompartment') By modelling enzymes as ellipsoids with axis length dependent on the maximum x,y and z dimensions of our enzyme complexes, this was broken down into the well-documented sand-packing problem. This enabled us to predict the maximum theoretical number of enzymes that can be packed into a microcompartment.
3. Effect of microcompartments on collision rates: (see
'Microcompartment rate of collision model') By using our stochastic diffusion models and discretizing the motion of our simulated particles, this compared the rate of collision of two particles when spatially constrained within a microcompartment versus in unconstrained motion.
 Figure 5
Figure 5
We have plotted the trajectories of two different molecules along random, stochastically driven discretized paths. What we illustrate here is that the rate of collision (marked in red) is substantially increased through the use of spatial constraints.
4. Stochastic diffusion of formaldehyde within microcompartments: (see
'Modelling the diffusion of formaldehyde inside the microcompartment') Stochastic diffusion of formaldehyde within cell: Building on the stochastic diffusion models developed previously, we then predicted how the concentration of formaldehyde within a cell would change over time given the restrictions imposed by the microcompartment.
5. Star-peptide model: (see
'The Star-Peptide Model') Our major collaboration with Unimelb iGEM involved modelling the effect of attaching multiple enzymes to a star peptide. This built upon the stochastic diffusion models developed earlier and represents an alternative method of reducing toxic intermediate accumulation to microcompartments.
 Figure 6
Figure 6
Plotted here is the logarithmic relationship between star peptide bond length and reaction rate. This was simulated for Melbourne iGEM and suggests that the rate of reaction will be inversely proportional to average peptide length to the power of four.
 "
"


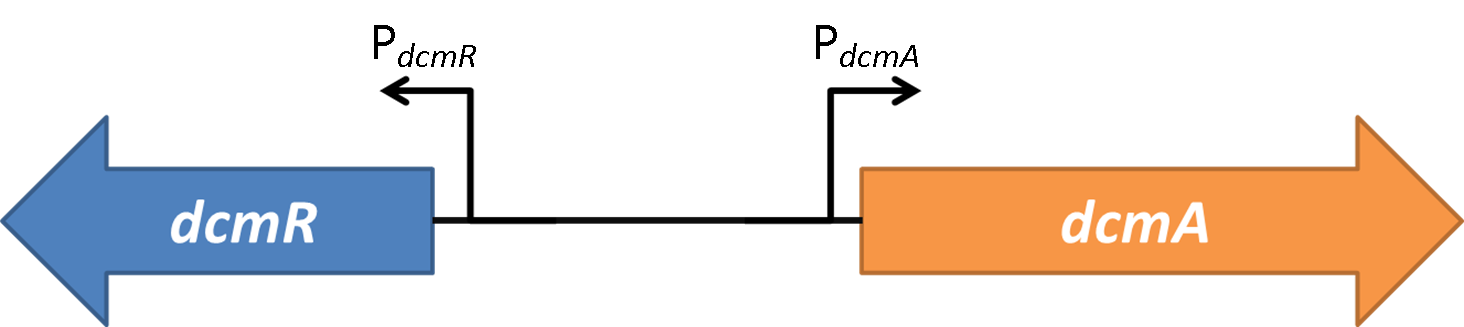





 Figure 2
Figure 2