Team:ETH Zurich/modeling/diffmodel
From 2014.igem.org
(→Reactions) |
(→Pattern developing) |
||
| (33 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{:Team:ETH Zurich/tpl/head|Diffusion model}} | {{:Team:ETH Zurich/tpl/head|Diffusion model}} | ||
| + | {{:Team:ETH Zurich/tpl/fortables}} | ||
{{:Team:ETH Zurich/tpl/read-more}} | {{:Team:ETH Zurich/tpl/read-more}} | ||
<center> | <center> | ||
| Line 14: | Line 15: | ||
=== Geometry and boundary conditions === | === Geometry and boundary conditions === | ||
| - | [[File:ETH Zurich Compartments Diffusion.png|float|500px|thumb|Millifluidic compartments used for the diffusion model]] | + | [[File:ETH Zurich Compartments Diffusion.png|float|500px|thumb|'''Figure 1''' Millifluidic compartments used for the diffusion model]] |
| Line 29: | Line 30: | ||
| - | [[File:ETHZ comsol geometry.png|center|610px|thumb|Geometry used for simulation on Comsol Multiphysics]] | + | [[File:ETHZ comsol geometry.png|center|610px|thumb|'''Figure 2''' Geometry used for simulation on Comsol Multiphysics]] |
<br> | <br> | ||
| - | In order to fulfill these conditions in Comsol Multiphysics, the cells are not drawn but instead, beads are considered as compartments with a certain density of cells. Rates of diffusion through the membrane are added as reaction rates and intracellular species are contained in beads via a | + | In order to fulfill these conditions in Comsol Multiphysics, the cells are not drawn but instead, beads are considered as compartments with a certain density of cells. Rates of diffusion through the membrane are added as reaction rates and intracellular species are contained in beads via a Neumann boundary condition applied to the surface of the beads, that is : |
| - | $$ \nabla C | + | $$ \nabla C \cdot \textbf{n} =0$$ |
$$\text{for all species except extracellular AHL}$$ | $$\text{for all species except extracellular AHL}$$ | ||
$$\text{for every vector n normal to the surface of a bead}$$ | $$\text{for every vector n normal to the surface of a bead}$$ | ||
| Line 72: | Line 73: | ||
=== Reactions === | === Reactions === | ||
| - | These reactions happen in every | + | These reactions happen in every bead of the pattern on the grid. |
$$ \begin{align} | $$ \begin{align} | ||
| Line 80: | Line 81: | ||
RLux+RLux &\leftrightarrow DRLux\\ | RLux+RLux &\leftrightarrow DRLux\\ | ||
DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ | DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ | ||
| - | P_{luxON}&\rightarrow P_{luxON}+mRNA_{GFP}\\ | + | P_{luxON}&\rightarrow P_{luxON}+mRNA_{GFP}+mRNA_{LuxI}\\ |
mRNA_{GFP}&\rightarrow GFP \\ | mRNA_{GFP}&\rightarrow GFP \\ | ||
| - | + | mRNA_{LuxI} &\rightarrow LuxI\\ | |
| + | AHLint &\rightarrow \\ | ||
| + | AHLext &\rightarrow \\ | ||
LuxR &\rightarrow \\ | LuxR &\rightarrow \\ | ||
RLux &\rightarrow\\ | RLux &\rightarrow\\ | ||
| Line 142: | Line 145: | ||
\begin{align*} | \begin{align*} | ||
\frac{d[AHLext]}{dt} &= \frac{N_0 N_m e^{rt}}{N_m+N_0(e^{rt}-1)} \alpha\ D_m \ (AHL_{int}-AHL_{ext}) -d_{AHLext}[AHL_{ext}]\\ | \frac{d[AHLext]}{dt} &= \frac{N_0 N_m e^{rt}}{N_m+N_0(e^{rt}-1)} \alpha\ D_m \ (AHL_{int}-AHL_{ext}) -d_{AHLext}[AHL_{ext}]\\ | ||
| - | \frac{d[AHLint]}{dt} &= Dm (AHL_{ext}-AHL_{int}) + k_{-RLux}[R_{Lux}]-k_{RLux}[ | + | \frac{d[AHLint]}{dt} &= Dm (AHL_{ext}-AHL_{int}) + k_{-RLux}[R_{Lux}]-k_{RLux}[AHL_{int}][LuxR]-d_{AHLint}[AHL_{int}]\\ |
\frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[AHL_{int}][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ | \frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[AHL_{int}][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ | ||
\frac{d[RLux]}{dt} &= k_{RLux}[AHL_{int}][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ | \frac{d[RLux]}{dt} &= k_{RLux}[AHL_{int}][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ | ||
\frac{d[mRNA_{GFP}]}{dt} &= \frac{k_{mRNA_{GFP}}[RLux]^2}{K_{mLux}^2 + [RLux]^2}- d_{mRNA_{GFP}} [mRNA_{GFP}]\\ | \frac{d[mRNA_{GFP}]}{dt} &= \frac{k_{mRNA_{GFP}}[RLux]^2}{K_{mLux}^2 + [RLux]^2}- d_{mRNA_{GFP}} [mRNA_{GFP}]\\ | ||
| - | \frac{d[GFP]}{dt} &= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP] | + | \frac{d[GFP]}{dt} &= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP] |
\end{align*} | \end{align*} | ||
$$ | $$ | ||
| Line 163: | Line 166: | ||
$$ [LuxR]_i=\frac{a_{LuxR}}{d_{LuxR}} $$ | $$ [LuxR]_i=\frac{a_{LuxR}}{d_{LuxR}} $$ | ||
The cells of the first row are induced by 10 μ M AHL just before they are encapsulated in alginate. Then, bead formation takes half-an-hour before these cells are added in the first well. During this half-an-hour AHL can diffuse out. Therefore initial conditions in the first cell completely depend on these previous steps. We have also simulated this bead preparation in order to get these initial conditions. | The cells of the first row are induced by 10 μ M AHL just before they are encapsulated in alginate. Then, bead formation takes half-an-hour before these cells are added in the first well. During this half-an-hour AHL can diffuse out. Therefore initial conditions in the first cell completely depend on these previous steps. We have also simulated this bead preparation in order to get these initial conditions. | ||
| + | |||
| + | [[File:ETHZ Beads in storage solution.jpg|center|300px|thumb|'''Figure 3''' Beads stored in calcium chloride, 10mM]] | ||
The geometry is a simple bead in a bigger compartment filled with calcium chloride. We look at the concentrations at the middle of the bead. Initial concentration of LuxR before bead diffusion starts is a classical steady state a<sub>LuxR</sub>/d<sub>LuxR</sub> | The geometry is a simple bead in a bigger compartment filled with calcium chloride. We look at the concentrations at the middle of the bead. Initial concentration of LuxR before bead diffusion starts is a classical steady state a<sub>LuxR</sub>/d<sub>LuxR</sub> | ||
| - | [[File:ETHZ Signaling molecules.png|600px|center]] | + | [[File:ETHZ Signaling molecules.png|600px|center|thumb|'''Figure 4''' Signaling molecules]] |
| - | [[File:ETHZ Regulators and GFP.png|600px|center]] | + | [[File:ETHZ Regulators and GFP.png|600px|center|thumb|'''Figure 5''' Regulators and GFP]] |
Extracellular AHL diffuses very fast through the membrane, which makes intracellular AHL increase, until both reach the same value and diffusion through the membrane reaches an equilibrium. From this point on AHL starts to bind to LuxR to form RLux, so AHL decreases, until RLux triggers enough production of LuxI which catalyses again AHL production, and makes AHL concentration become stable. | Extracellular AHL diffuses very fast through the membrane, which makes intracellular AHL increase, until both reach the same value and diffusion through the membrane reaches an equilibrium. From this point on AHL starts to bind to LuxR to form RLux, so AHL decreases, until RLux triggers enough production of LuxI which catalyses again AHL production, and makes AHL concentration become stable. | ||
| - | After 30 minutes, | + | After 30 minutes, all LuxR is bound to AHL and converted to RLux, so that we have |
| - | $$ [LuxR]_i= | + | $$ [LuxR]_i= 0nM$$ |
| - | $$ [RLux]_i= | + | $$ [RLux]_i= 200 nM$$ |
| + | $$ [AHLint]_i=[AHLint]_i=2 μ M$$ | ||
RLux has already started to trigger the production of LuxI and GFP, so that we have | RLux has already started to trigger the production of LuxI and GFP, so that we have | ||
| - | $$ [mRNAGFP]_i = | + | $$ [mRNAGFP]_i = 40nM$$ |
| - | $$ [GFP]_i = | + | $$ [GFP]_i = 900nM$$ |
| - | $$ [mRNALuxI]_i = | + | $$ [mRNALuxI]_i = 40nM$$ |
| - | $$ [LuxI]_i = | + | $$ [LuxI]_i = 16000nM$$ |
<html><div id='Estimation'></html> | <html><div id='Estimation'></html> | ||
| + | |||
=== Estimation of parameters from literature === | === Estimation of parameters from literature === | ||
| - | The initial number of beads is 10 million. According to Lars Müller's master thesis<sup>[[Team:ETH_Zurich/project/references|[29]]]</sup>, in picoliter beads, cells doubling time is 30 minutes. Here we are using beads with a volume in the microliter range. Because of bead volume, oxygen and nutrients are much less accessible. Therefore, we multiplied this doubling time by 4. We have a | + | The initial number of beads is 10 million. According to Lars Müller's master thesis<sup>[[Team:ETH_Zurich/project/references|[29]]]</sup>, in picoliter beads, cells doubling time is 30 minutes. Here we are using beads with a volume in the microliter range. Because of bead volume, oxygen and nutrients are much less accessible. Therefore, we multiplied this doubling time by 4. We have a growth rate of 0.006 min<sup>-1</sup> which is still above the growth rate in anaerobic conditions (0.004 min<sup>-1</sup> according to [http://bionumbers.hms.harvard.edu/search.aspx?log=y&task=searchbytrmorg&trm=growth+rate+e+coli&org= Bionumbers]) |
| - | + | In the conditions of lack of oxygen and nutrients where our cells are, we consider that they might at maximum double or triple. So we take 8 . 10<sup>7</sup> cells per bead for N<sub>m</sub>. | |
| Line 198: | Line 205: | ||
| - | <html></ | + | <html></div></html> |
| Line 212: | Line 219: | ||
The background in our experimental setup is very high and this is high we see actual fluorescence appear only after 11 hours. In order to account for this, we also set up a background in the simulated pattern by adjusting the scale. | The background in our experimental setup is very high and this is high we see actual fluorescence appear only after 11 hours. In order to account for this, we also set up a background in the simulated pattern by adjusting the scale. | ||
| - | ----- | + | |
| - | ------------------ | + | {|class="wikitable" style="background-color: white; text-align:center; width:auto; margin: auto; font-size:10pt;" |
| + | |colspan="2" style='font-size:10pt';text-align:left|{{:Team:ETH_Zurich/Templates/Video|width=1080px|id=video3|ratio=1920/720|srcMP4=<html>https://static.igem.org/mediawiki/2014/b/b1/ETH_Zurich_2014_signal_propagation_with_simulation.mp4</html>|poster=<html>https://static.igem.org/mediawiki/2014/6/69/ETH_Zurich_2014_signal_propagation_with_simulation_preview.png</html>}} | ||
| + | |- | ||
| + | |colspan="2" style='font-size:10pt';text-align:left|'''Video 1''' '''Row wise, self-propagating [https://2014.igem.org/Team:ETH_Zurich/project/background/biotools#Quorum_Sensing cell-to-cell communication] of ''E. coli'' cells confined in [https://2014.igem.org/Team:ETH_Zurich/lab/bead alginate beads] (d=3 mm, initially 10<sup>7</sup> cells/bead) on a [https://2014.igem.org/Team:ETH_Zurich/lab/chip custom-made millifluidic PDMS chip].''' | ||
| + | |- | ||
| + | |style="width:50%"|All fluorescent cells contained [https://2014.igem.org/Team:ETH_Zurich/expresults/rr#Riboregulators riboregulated] sfGFP followed by [http://parts.igem.org/Part:BBa_C0161 LuxI (BBa_C0161)] together under the control of the [http://parts.igem.org/Part:BBa_R0062 pLux promoter (BBa_R0062)], and [http://parts.igem.org/Part:BBa_J23100 constitutively (BBa_J23100)] expressed [http://parts.igem.org/Part:BBa_C0062 LuxR (BBa_C0062)]. LuxI catalyzes the production of the autoinducer 3OC6-HSL, which is then diffusing from cell to cell. For initialization, the cells in one bead of the top row were induced with 3OC6-HSL before encapsulation. Imaging was implemented with a [https://2014.igem.org/Team:ETH_Zurich/lab/protocols#Biostep_Dark-Hood_DH-50.E2.84.A2__and_the_Argus-X1.E2.84.A2_software Biostep Dark-Hood DH-50 (Argus X1 software)] fitted with a Canon EOS 500D DSLR camera and a fluorescence filter (545 nm filter). Pictures were usually taken every 2 min at an excitation wavelength of 470 nm with the standard Canon EOS Utility software. Time-lapse movies were created with Adobe After Effects CC software. 1950x faster than real-time, the video shown starts 10 h after the initiation of the experiment (however the time scale shown corresponds to minutes after loading of the chip). For precise experimental setup, check the [https://2014.igem.org/Team:ETH_Zurich/expresults#Diffusion Results] page. | ||
| + | ||Simulation of the propagation of the pattern in the millifluidic chip. [http://www.comsol.com/comsol-multiphysics Comsol Multiphysics Simulation software] was used in order to simulate a detailed diffusion model including quorum sensing steps in colonies and cell growth. Overall GFP concentration in beads has been scaled in order to account for the high background of the experimental setup. Green Fluorescence Protein is produced earlier in the wells, but can be seen only above a certain threshold.<br>Accurate prediction of experimental data by the model has been achieved, with parameters from our own fittings or from the literature. Experimental observation combined with simulation enables to show that a pattern is able to develop in the millifluidic chip in a reasonable time scale. | ||
| + | |} | ||
=== Dynamics by row === | === Dynamics by row === | ||
| Line 221: | Line 235: | ||
<br> | <br> | ||
| - | + | [[File:ETHZ AHL-regulators-pattern.png|center|900px|thumb|'''Figure 6''']] | |
| - | + | ||
| - | [[File:ETHZ AHL-regulators-pattern.png|center]] | + | |
| - | + | ||
<br> | <br> | ||
| Line 232: | Line 243: | ||
<br> | <br> | ||
| - | + | [[File:ETHZ GFP in beads.png|600px|center|thumb|'''Figure 7''' GFP in beads ]] | |
| - | [[File:ETHZ GFP in beads.png|600px|center]] | + | [[File:ETHZ GFP in single cell.png|600px|center|thumb|'''Figure 8''' GFP in single cell]] |
| - | [[File:ETHZ GFP in single cell.png|600px|center]] | + | |
| - | + | ||
{{:Team:ETH_Zurich/tpl/topbutton|green}} | {{:Team:ETH_Zurich/tpl/topbutton|green}} | ||
Latest revision as of 01:13, 18 October 2014
Diffusion model
Model
The main experiment for investigating diffusion is a propagation of the whole pattern through the chip via the quorum sensing module only. We have used beads containing cells which are able to sense luxAHL, produce GFP when they sense it, and amplify the signal for the next row. The combination of the quorum sensing module with diffusion enables to check that cells will amplify the signal enough from one row to the next one, and to check what would be the time scale of the pattern formation. We used a reaction-diffusion model to combine quorum sensing reactions and diffusion.
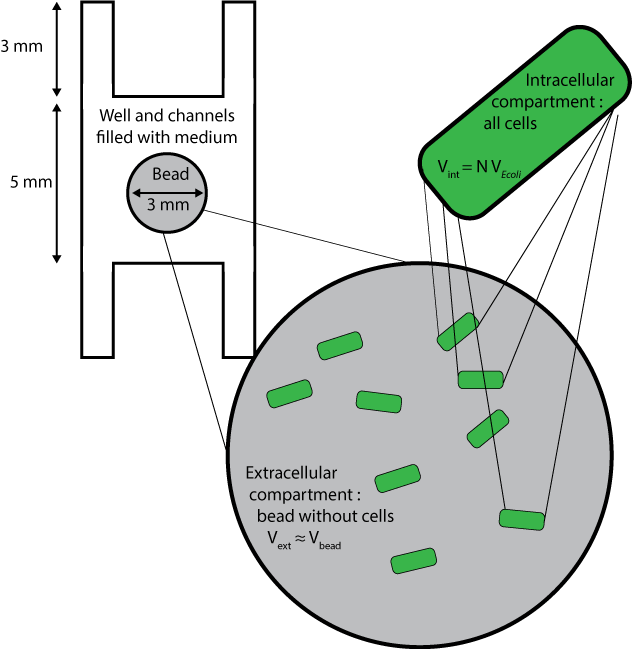
Geometry and boundary conditions
Three different compartments are considered :
- The wells and channels, which are filled with liquid medium and where extracellular AHL only can diffuse, with its diffusion coefficient D, and degrade with the degradation rate dAHLext.
- The beads without the cells inside them, whose volumes are approximated to the volume of beads themselves, and where extracellular AHL only can degrade and diffuse, with an a priori different diffusion coefficient Cbeads* DAHLext.
- The cells, which are considered altogether as one compartment, and which contains all species except extracellular AHL.
In order to fulfill these conditions in Comsol Multiphysics, the cells are not drawn but instead, beads are considered as compartments with a certain density of cells. Rates of diffusion through the membrane are added as reaction rates and intracellular species are contained in beads via a Neumann boundary condition applied to the surface of the beads, that is : $$ \nabla C \cdot \textbf{n} =0$$ $$\text{for all species except extracellular AHL}$$ $$\text{for every vector n normal to the surface of a bead}$$
Species
| Name | Description |
|---|---|
| AHLint | LuxAHL inside cells |
| AHLext | LuxAHL outside cells |
| LuxR | Constitutively expressed regulator protein that can bind LuxAHL and stimulate transcription of GFP. |
| RLux | LuxR and LuxAHL complex which can dimerize. |
| mRNAGFP | mRNA for Green fluorescent protein which is produced when the cells are ON. |
| GFP | Green fluorescent protein which is produced when the cells are ON. |
| mRNALuxI | mRNA for LuxI which is produced when the cells are ON. |
| LuxI | Enzyme catalysing the production of LuxAHL from SAM and ACP. |
Reactions
These reactions happen in every bead of the pattern on the grid.
$$ \begin{align} \emptyset&\rightarrow LuxR \\ AHLext & \leftrightarrow AHLint\\ AHLint+LuxR & \leftrightarrow RLux\\ RLux+RLux &\leftrightarrow DRLux\\ DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ P_{luxON}&\rightarrow P_{luxON}+mRNA_{GFP}+mRNA_{LuxI}\\ mRNA_{GFP}&\rightarrow GFP \\ mRNA_{LuxI} &\rightarrow LuxI\\ AHLint &\rightarrow \\ AHLext &\rightarrow \\ LuxR &\rightarrow \\ RLux &\rightarrow\\ mRNA_{GFP} &\rightarrow\\ mRNA_{LuxI} &\rightarrow\\ GFP &\rightarrow \\ LuxI &\rightarrow \end{align}$$
Equations
Deriving diffusion rates
We are using a reaction-diffusion model, which means that for internal and external AHL species which diffuse, we have to include a diffusion rate in addition to reaction rates from the quorum sensing module :
$$\frac{d[AHL]}{dt}=\mathcal{Diff}(AHL)+\mathcal{R}(AHL)$$
In the extracellular compartment of the bead, Diff(AHL) is made of two components : a diffusion rate due to isotropic diffusion of AHL, and a rate due to diffusion of AHL through the cell membrane. In the intracellular compartment, much smaller compared to the extracellular, we can consider that the only component is the rate of diffusion through the cell membrane.
According to Fick's law of diffusion, the flow of AHL Φ(AHLint) (number of molecules per second) from the bead into the cells and the flow of AHL Φ (AHLext) from cells into the bead are $$\Phi(AHL_{int}) = N \sigma \mathcal{A} ([AHL_{ext}]-[AHL_{int}]) \\ \Phi(AHL_{ext}) = N \sigma \mathcal{A} ([AHL_{int}]-[AHL_{ext}])$$ $$\text{where }\sigma \text { is the membrane permeability}$$ $$\mathcal{A} \text{ is the area of the membrane}$$ $$N \text{ is the number of cells per bead.}$$
Thus the diffusion rate of internal AHL (concentration per second) is :
$$ Diff(AHL_{int})=\frac{N \sigma \mathcal{A}}{V_{int}} ([AHL_{ext}]-[AHL_{int}])=D_m ([AHL_{ext}-[AHL_{int}]) $$
$$\text{where } V_{int} \text{ is the total volume of all cells}$$
$$D_m \text{ is a lumped coefficient for diffusion through the membrane}$$
and the diffusion rate of external AHL is $$ \begin{align*} Diff(AHL_{ext})&=D_{AHLext}\nabla^2[AHLext]+\frac{N \sigma \mathcal{A}}{V_{bead}} ([AHL_{ext}]-[AHL_{int}]\\ &= D_{AHLext}\nabla^2[AHLext]+\frac{N V_{E.coli}}{V_{bead}}D_m([AHL_{ext}]-[AHL_{int}]) \\ &= D_{AHLext}\nabla^2[AHLext]+N \alpha D_m([AHL_{ext}]-[AHL_{int}]) \end{align*}$$
$$ \text{where } \alpha = \frac{V_{E.coli}}{V_{bead}}$$ $$V_{E.coli} \text{ is the volume of one cell }$$ $$V_{bead}\text{ is the volume of one bead.} $$
Modeling growth
We have used a logistic growth function for the number of cells: $$ N = \frac{N_0 N_m e^{rt}}{N_m+N_0(e^{rt}-1)} $$ $$\text{where } N_0 \text{ is the initial number of cells per bead} $$ $$N_m \text{ is the maximum number of cells per bead}$$ $$r \text{ is the growth rate }$$
Set of equations used
$$ \begin{align*} \frac{d[AHLext]}{dt} &= \frac{N_0 N_m e^{rt}}{N_m+N_0(e^{rt}-1)} \alpha\ D_m \ (AHL_{int}-AHL_{ext}) -d_{AHLext}[AHL_{ext}]\\ \frac{d[AHLint]}{dt} &= Dm (AHL_{ext}-AHL_{int}) + k_{-RLux}[R_{Lux}]-k_{RLux}[AHL_{int}][LuxR]-d_{AHLint}[AHL_{int}]\\ \frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[AHL_{int}][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ \frac{d[RLux]}{dt} &= k_{RLux}[AHL_{int}][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ \frac{d[mRNA_{GFP}]}{dt} &= \frac{k_{mRNA_{GFP}}[RLux]^2}{K_{mLux}^2 + [RLux]^2}- d_{mRNA_{GFP}} [mRNA_{GFP}]\\ \frac{d[GFP]}{dt} &= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP] \end{align*} $$
Parameter estimation
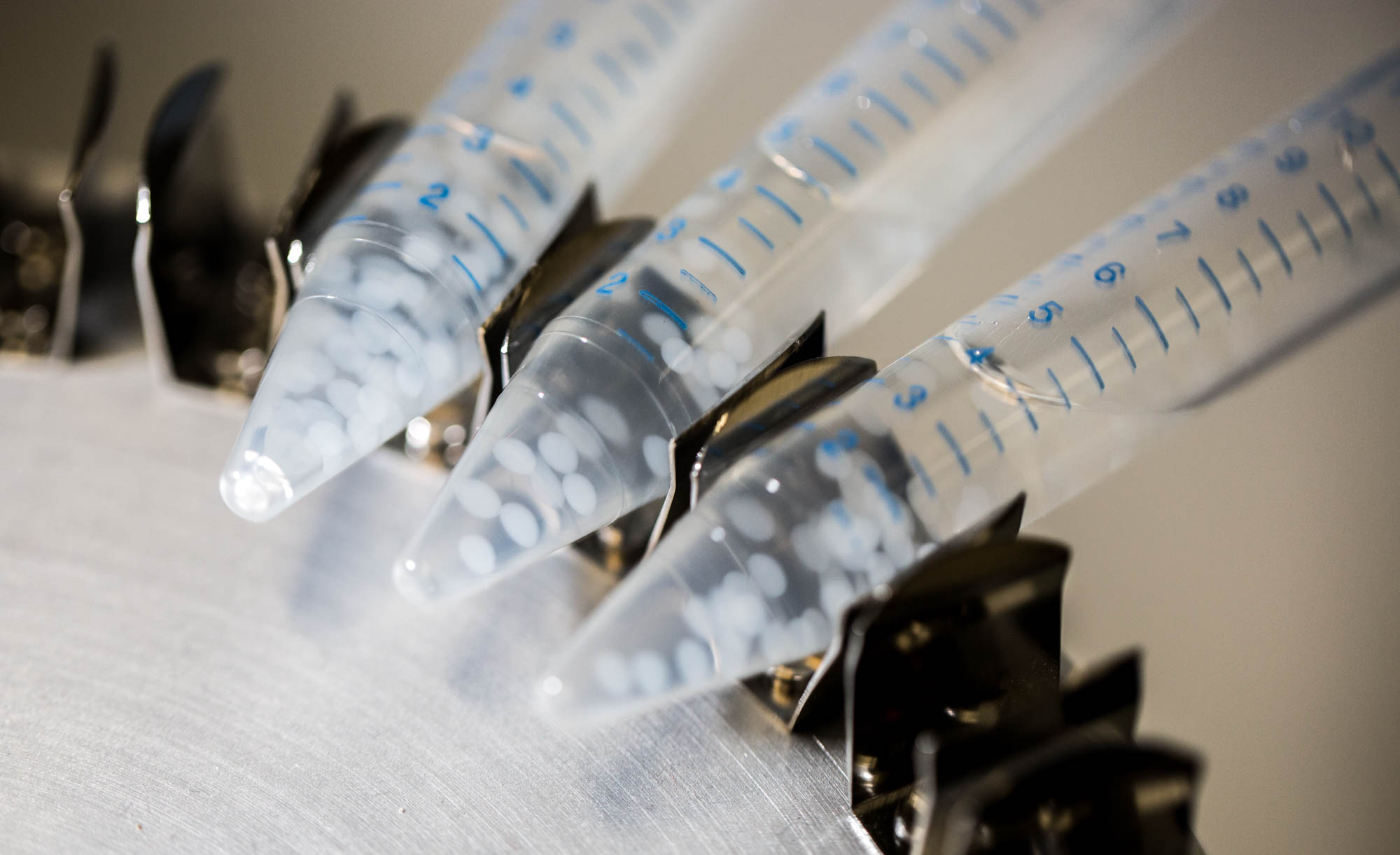
Initial conditions determined by bead preparation step
Non-induced cells, that is all cells except the one from the middle well of the first row have an initial LuxR concentration of LuxR due to constitutive production and degradation : $$ [LuxR]_i=\frac{a_{LuxR}}{d_{LuxR}} $$ The cells of the first row are induced by 10 μ M AHL just before they are encapsulated in alginate. Then, bead formation takes half-an-hour before these cells are added in the first well. During this half-an-hour AHL can diffuse out. Therefore initial conditions in the first cell completely depend on these previous steps. We have also simulated this bead preparation in order to get these initial conditions.
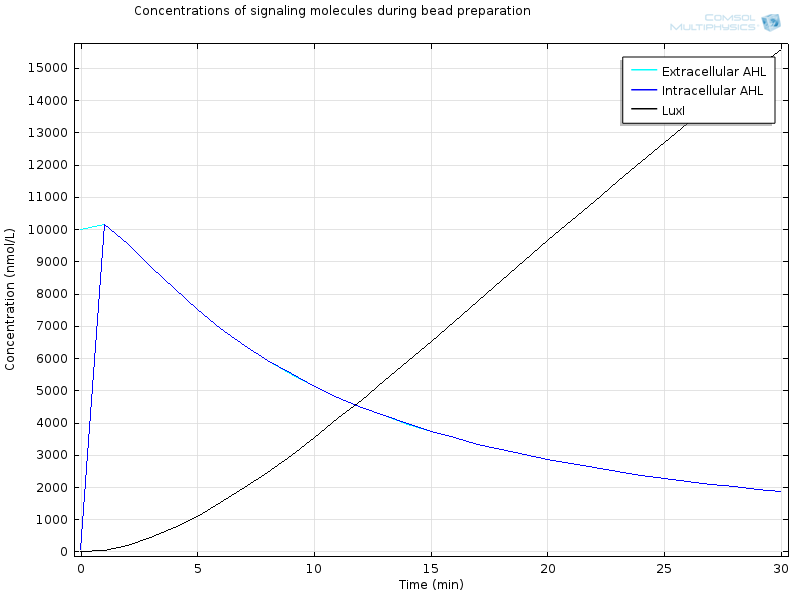
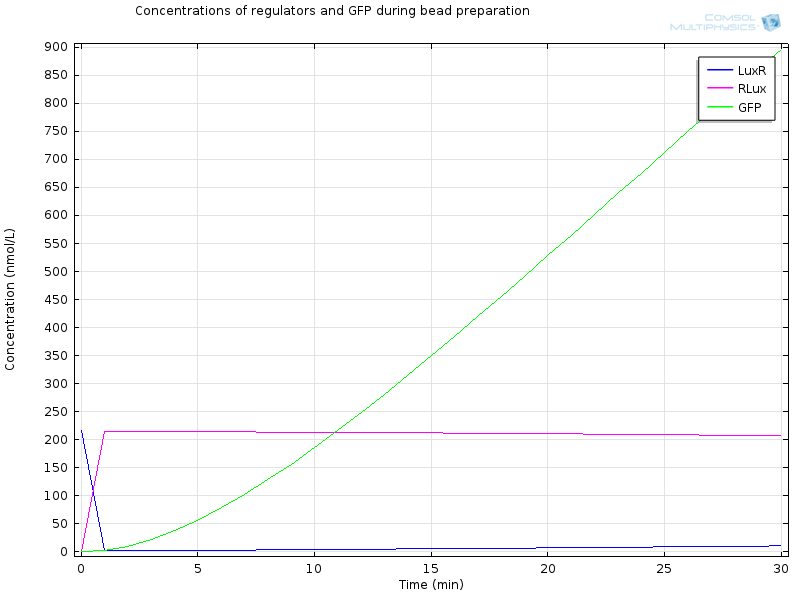
The geometry is a simple bead in a bigger compartment filled with calcium chloride. We look at the concentrations at the middle of the bead. Initial concentration of LuxR before bead diffusion starts is a classical steady state aLuxR/dLuxR
Extracellular AHL diffuses very fast through the membrane, which makes intracellular AHL increase, until both reach the same value and diffusion through the membrane reaches an equilibrium. From this point on AHL starts to bind to LuxR to form RLux, so AHL decreases, until RLux triggers enough production of LuxI which catalyses again AHL production, and makes AHL concentration become stable.
After 30 minutes, all LuxR is bound to AHL and converted to RLux, so that we have $$ [LuxR]_i= 0nM$$ $$ [RLux]_i= 200 nM$$ $$ [AHLint]_i=[AHLint]_i=2 μ M$$
RLux has already started to trigger the production of LuxI and GFP, so that we have $$ [mRNAGFP]_i = 40nM$$ $$ [GFP]_i = 900nM$$ $$ [mRNALuxI]_i = 40nM$$ $$ [LuxI]_i = 16000nM$$
Estimation of parameters from literature
The initial number of beads is 10 million. According to Lars Müller's master thesis[29], in picoliter beads, cells doubling time is 30 minutes. Here we are using beads with a volume in the microliter range. Because of bead volume, oxygen and nutrients are much less accessible. Therefore, we multiplied this doubling time by 4. We have a growth rate of 0.006 min-1 which is still above the growth rate in anaerobic conditions (0.004 min-1 according to [http://bionumbers.hms.harvard.edu/search.aspx?log=y&task=searchbytrmorg&trm=growth+rate+e+coli&org= Bionumbers])
In the conditions of lack of oxygen and nutrients where our cells are, we consider that they might at maximum double or triple. So we take 8 . 107 cells per bead for Nm.
According to Kaplan's paper[28], LuxAHL diffuses very fast through the membrane : "This report demonstrates that V. fischeri and E. coli are freely permeable to autoinducer. When autoinducer was added to cell suspensions, internal concentrations approximated external concentrations, and equilibration was rapid (within 20 s)."
Therefore we take 100 min-1 for Dm, and indeed external and internal concentrations become very quickly almost equal.
According to Hannoun et al[30], diffusion coefficient of glucose in 2% calcium alginate (which is the material of our beads) is the same as in water. 3O-C6HSL and glucose have similar molecular weights (199.2 g/mol for 3O-C6HSL and 180.16 g/mol for glucose). Therefore we can consider that 3O-C6HSL will diffuse the same way and we took Cbead=1.
Results
Pattern developing
The developing pattern shows that every row senses the signal coming from above, amplifies it and is capable to send a signal to the next row, which is high enough to enable propagation until the bottom of the grid. We can see that the dynamics of the model are very well fitted to experimental conditions.
The background in our experimental setup is very high and this is high we see actual fluorescence appear only after 11 hours. In order to account for this, we also set up a background in the simulated pattern by adjusting the scale.
|
| |
| Video 1 Row wise, self-propagating cell-to-cell communication of E. coli cells confined in alginate beads (d=3 mm, initially 107 cells/bead) on a custom-made millifluidic PDMS chip. | |
| All fluorescent cells contained riboregulated sfGFP followed by [http://parts.igem.org/Part:BBa_C0161 LuxI (BBa_C0161)] together under the control of the [http://parts.igem.org/Part:BBa_R0062 pLux promoter (BBa_R0062)], and [http://parts.igem.org/Part:BBa_J23100 constitutively (BBa_J23100)] expressed [http://parts.igem.org/Part:BBa_C0062 LuxR (BBa_C0062)]. LuxI catalyzes the production of the autoinducer 3OC6-HSL, which is then diffusing from cell to cell. For initialization, the cells in one bead of the top row were induced with 3OC6-HSL before encapsulation. Imaging was implemented with a Biostep Dark-Hood DH-50 (Argus X1 software) fitted with a Canon EOS 500D DSLR camera and a fluorescence filter (545 nm filter). Pictures were usually taken every 2 min at an excitation wavelength of 470 nm with the standard Canon EOS Utility software. Time-lapse movies were created with Adobe After Effects CC software. 1950x faster than real-time, the video shown starts 10 h after the initiation of the experiment (however the time scale shown corresponds to minutes after loading of the chip). For precise experimental setup, check the Results page. | Simulation of the propagation of the pattern in the millifluidic chip. [http://www.comsol.com/comsol-multiphysics Comsol Multiphysics Simulation software] was used in order to simulate a detailed diffusion model including quorum sensing steps in colonies and cell growth. Overall GFP concentration in beads has been scaled in order to account for the high background of the experimental setup. Green Fluorescence Protein is produced earlier in the wells, but can be seen only above a certain threshold. Accurate prediction of experimental data by the model has been achieved, with parameters from our own fittings or from the literature. Experimental observation combined with simulation enables to show that a pattern is able to develop in the millifluidic chip in a reasonable time scale. |
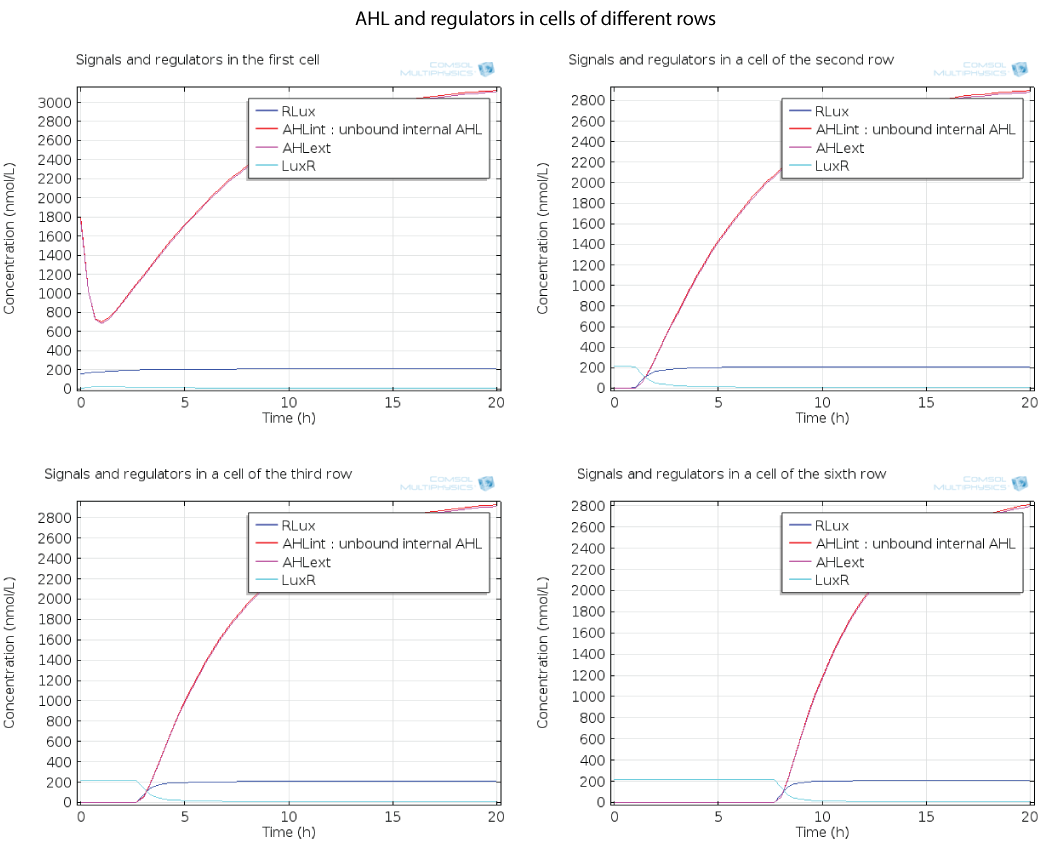
Dynamics by row
Here you can see the quorum sensing mechanism happening in several rows at different moments. The first colony has a high initial concentration of AHL so at the beginning, AHL diffuses quickly out of the first colony. However as the first cell is strongly induced because of this AHL, a positive feedback is produced which will enable AHL concentration to reach a steady state. The colonies in the row below receive AHL progressively as opposed to the first colony which had an initial concentration, so the feedback in these colonies below has the time to happen immediately when AHL is received, and this is why AHL increases so fast in these colonies.
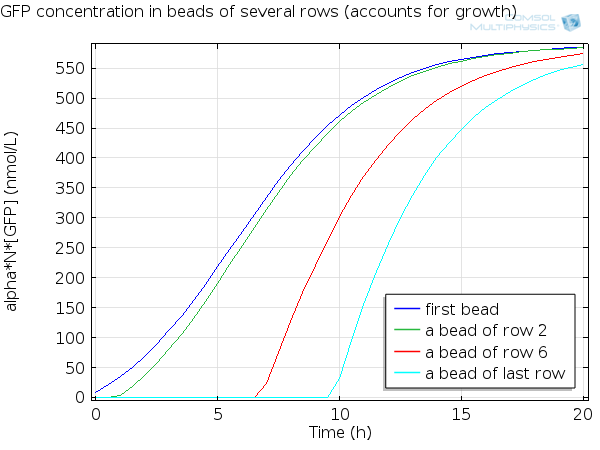
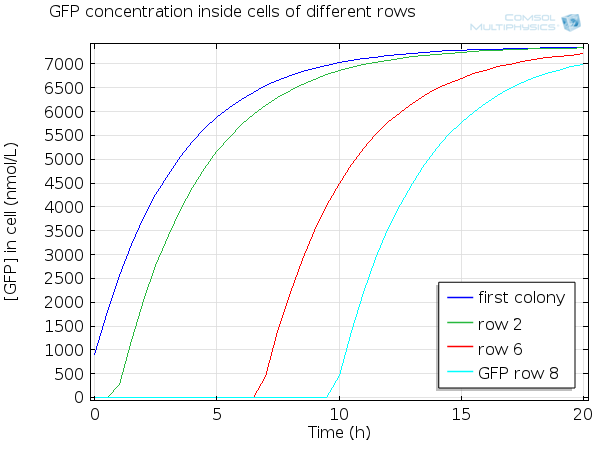
For simulation of the pattern, in order to be able to simulate fluorescence of the beads which is influenced by cell growth, we had to plot the concentration of GFP overall in a bead as opposed to the concentration of GFP in cells. Here we compare concentration of GFP in cells (doesn't account for growth) and overall concentration of GFP in a bead (accounts for growth) :
 "
"