Team:ETH Zurich/modeling/xor
From 2014.igem.org
m (→Principle) |
(→Deterministic simulation) |
||
| (31 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{:Team:ETH Zurich/tpl/head|XOR Gate}} | {{:Team:ETH Zurich/tpl/head|XOR Gate}} | ||
| + | {{:Team:ETH Zurich/tpl/fortables}} | ||
| + | <center> | ||
| + | {{:Team:ETH Zurich/tpl/scrollbutton3|Model|blue}} | ||
| + | {{:Team:ETH Zurich/tpl/scrollbuttontworows|Transfer|Function|red}} | ||
| + | </center> | ||
| - | <html><article></html> | + | <html><article id="Model"></html> |
== Model == | == Model == | ||
| Line 9: | Line 14: | ||
=== XOR Logic Gate === | === XOR Logic Gate === | ||
| - | + | We consider a binary exclusive or (XOR) logic gate, with two inputs and one output. | |
| - | + | <br/> | |
| - | + | <br/> | |
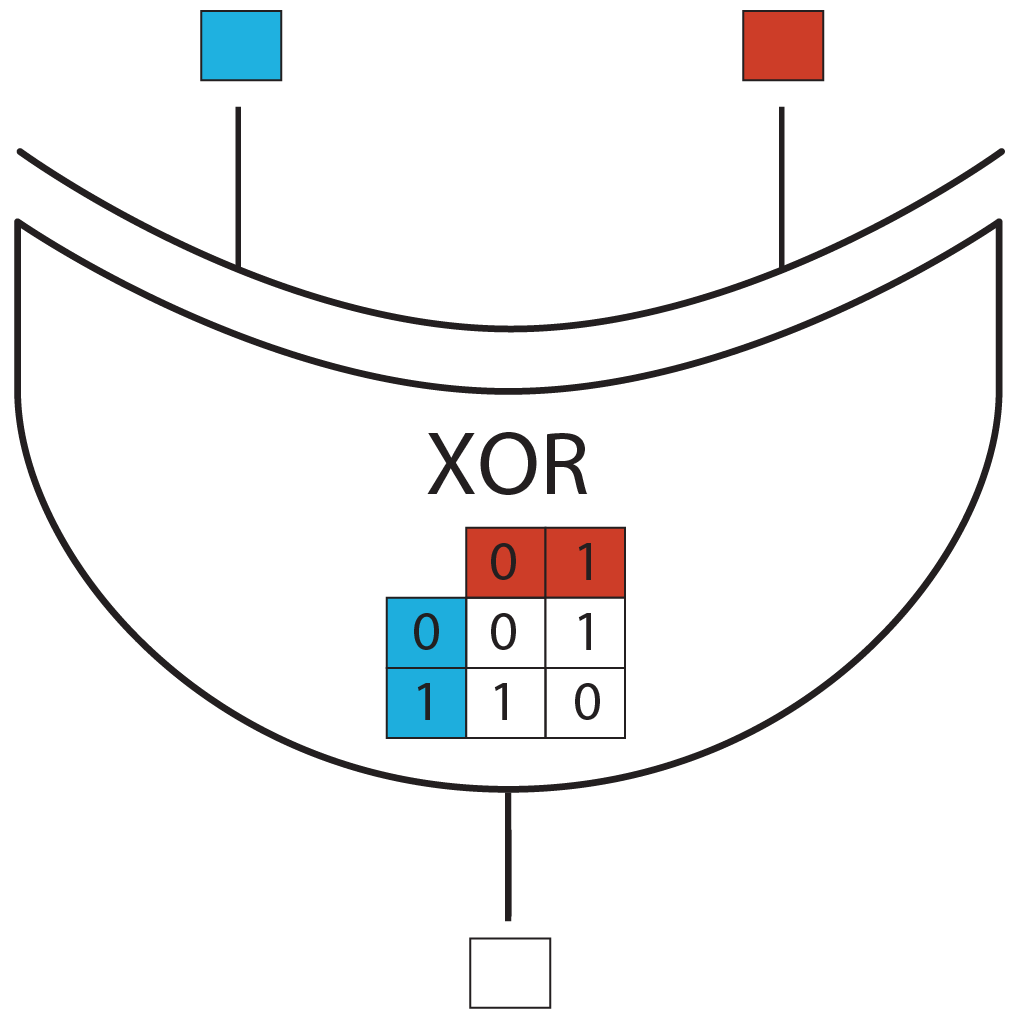
| + | [[File:ETH_Zurich_XOR_Logic_Gate.png|400px|center|thumb|'''Figure 1''' Truth table of the XOR logic gate.]] | ||
=== Biological Principles === | === Biological Principles === | ||
| Line 24: | Line 30: | ||
<br> | <br> | ||
<br> | <br> | ||
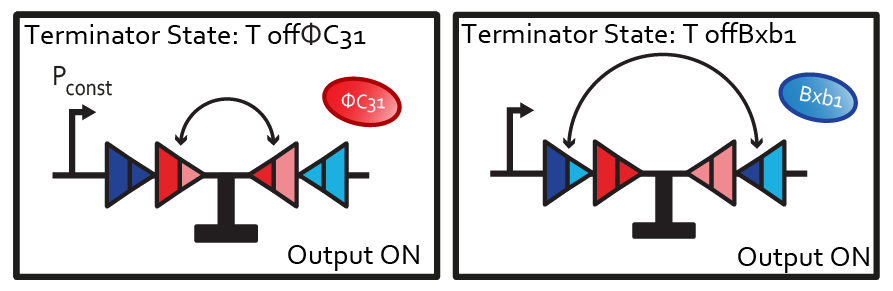
| - | The terminator can be flipped once if either DBxb1 or ΦC31 is present. The state T<sub>off</sub> can be | + | The terminator can be flipped once if either DBxb1 or ΦC31 is present. The state T<sub>off</sub> can be reached via two possible transitions. We further decompose it into two different states: T<sub>offBxb1</sub>(flipping due to presence of Bxb1) and T<sub>offΦC31</sub>(flipping due to presence of ΦC31). |
| + | <br> | ||
| + | <br> | ||
| + | [[File:ETH Zurich XOR Toffs.png|400px|center|thumb|'''Figure 2''' Decomposition of the on output into two terminator states.]] | ||
<br> | <br> | ||
<br> | <br> | ||
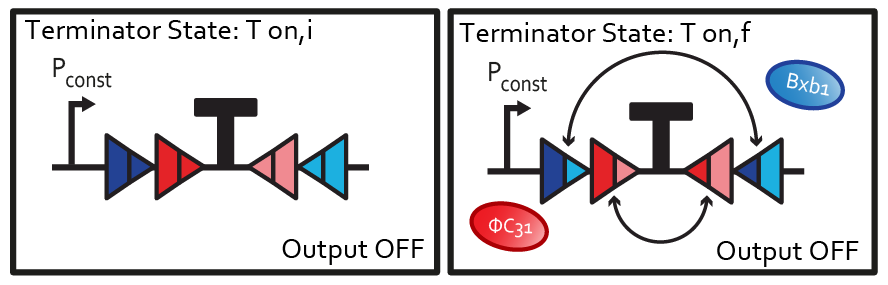
Flipping by integrases is irreversible. The initial state, in which the terminator is on, is different from the state after two switches. From this last state, no further evolution of the system is possible. Therefore, we decompose the T<sub>on</sub> into two different states: T<sub>on,i</sub>(initial state of the system, no flipping) and T<sub>on,f</sub>(final state of the system after two flips). | Flipping by integrases is irreversible. The initial state, in which the terminator is on, is different from the state after two switches. From this last state, no further evolution of the system is possible. Therefore, we decompose the T<sub>on</sub> into two different states: T<sub>on,i</sub>(initial state of the system, no flipping) and T<sub>on,f</sub>(final state of the system after two flips). | ||
| + | <br> | ||
| + | <br> | ||
| + | [[File:ETH Zurich XOR Tons.png|400px|center|thumb|'''Figure 3''' Decomposition of the off output into two terminator states.]] | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | === XOR bio''logic'' gate === | ||
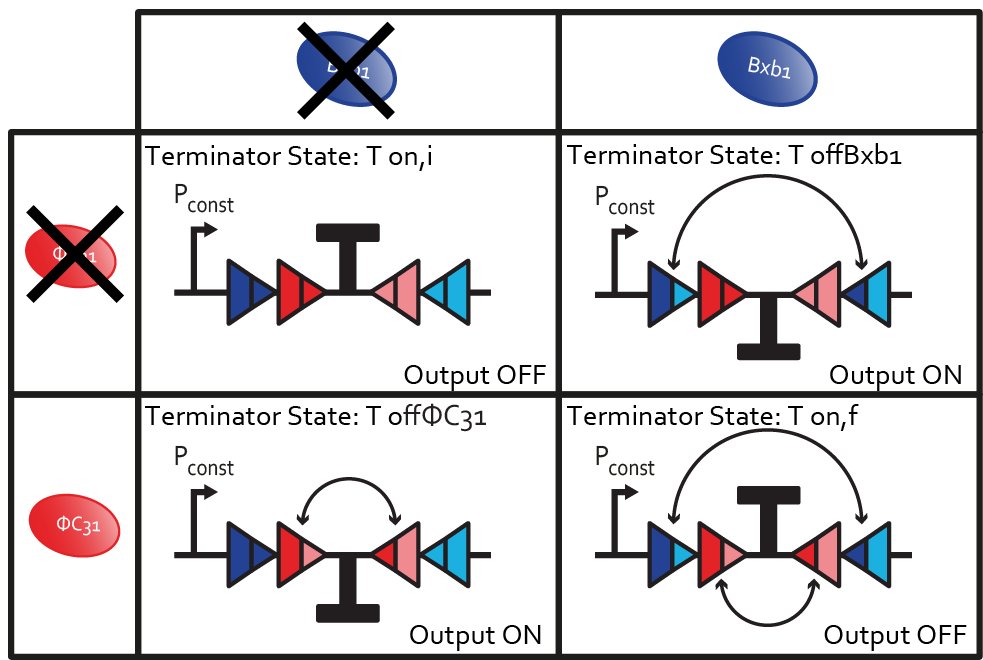
| - | '' | + | [[File:ETH_Zurich_XOR_Biologic_Gate.png|center|600px|thumb|'''Figure 4''' Truth table of the XOR biologic gate: Summary of the model, coupled with the biological explanation.]] |
=== Other Chemical Species === | === Other Chemical Species === | ||
| Line 59: | Line 75: | ||
=== Reactions === | === Reactions === | ||
| - | The following reactions are valid for the strain producing LasAHL as output (It corresponds to the blue cells [https://2014.igem.org/Team:ETH_Zurich/project/overview#Implementation_in_E._Coli here]) | + | The following reactions are valid for the strain producing LasAHL as output (It corresponds to the blue cells [https://2014.igem.org/Team:ETH_Zurich/project/overview#Implementation_in_E._Coli here]). |
| - | $$\begin{align*} | + | |
| + | <html><center></html>$$\begin{align*} | ||
SA_{Bxb1}+SA_{Bxb1}+T_{on,i}& \rightarrow T_{offBxb1}+ SF_{Bxb1}+SF_{Bxb1}\\ | SA_{Bxb1}+SA_{Bxb1}+T_{on,i}& \rightarrow T_{offBxb1}+ SF_{Bxb1}+SF_{Bxb1}\\ | ||
T_{offBxb1} &\rightarrow T_{offBxb1} + mRNA_{GFP} + mRNA_{LasI} \\ | T_{offBxb1} &\rightarrow T_{offBxb1} + mRNA_{GFP} + mRNA_{LasI} \\ | ||
| Line 73: | Line 90: | ||
GFP &\rightarrow \emptyset\\ | GFP &\rightarrow \emptyset\\ | ||
LasI&\rightarrow \emptyset | LasI&\rightarrow \emptyset | ||
| - | \end{align*}$$ | + | \end{align*}$$<html></center></html> |
| + | |||
| + | To have the equivalent for the strain producing LuxAHL as output, it suffices to replace every occurence of LasI by LuxI. | ||
<html></article></html> | <html></article></html> | ||
| + | |||
| + | <html><article id="Transfer"></html> | ||
| + | |||
| + | == Transfer Function == | ||
| + | |||
| + | === Determistic Differential Equations === | ||
| + | We modeled the XOR gate module deterministically. Thus, we considered a continuous approximation of variables, like the number of integrases-DNA binding sites or the number of terminator. We wrote them as concentration. We do not take the species LasI and mRNA<sub>LasI</sub> into account because they are only produced by the XOR biologic gate and GFP is another product of this biologic gate that can be read out. | ||
| + | $$\begin{align*} | ||
| + | \frac{d[T_{on,i}]}{dt}&= -k_{ToffBxb1}[T_{on,i}][SA_{Bxb1}]^2 -k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 \\ | ||
| + | \frac{d[T_{offBxb1}]}{dt}&=k_{ToffBxb1} [T_{on,i}][SA_{Bxb1}]^2 - k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2\\ | ||
| + | \frac{d[T_{off\phi C31}]}{dt}&=k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 - k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\ | ||
| + | \frac{d[T_{on,f}]}{dt}&= k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2 + k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\ | ||
| + | \frac{d[mRNA_{GFP}]}{dt}&= k_{mRNA_{GFP}} (\frac{[T_{offBxb1}]}{\theta + [T_{offBxb1}]} + \frac{[T_{off\phi C31}]}{\theta + [T_{off\phi C31}]}) - d_{mRNA_{GFP}}[mRNA_{GFP}]\\ | ||
| + | \frac{d[GFP]}{dt}&= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP]\\ | ||
| + | \end{align*}$$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | As there is a strong codon bias in both integrases' seuquences <sup>[[Team:ETH_Zurich/project/references|[14]]]</sup>, the flipping parameters were assumed such that they would not be a rate limiting step. (see the [https://2014.igem.org/Team:ETH_Zurich/modeling/parameters parameter pages]) | ||
| + | <br/> | ||
| + | <br/> | ||
| + | |||
| + | === Deterministic simulation === | ||
| + | At steady state, the transfer function obtained by simulation is shown on the next figure. It is remarkable to see that even a little amount of one integrase is sufficient to switch the XOR gate on. | ||
| + | <br> | ||
| + | [[File:ETHZ_XORmodule.png|center|600px|thumb|'''Figure 5''' The behaviour of XOR module as a function of activated Bxb1 sites (SABxb1) and ΦC31 sites (SAΦC31). The XOR behaviour is continuous since we modelled it deterministically.]] | ||
| + | |||
| + | <html></article></html> | ||
| + | |||
{{:Team:ETH Zurich/tpl/foot}} | {{:Team:ETH Zurich/tpl/foot}} | ||
Latest revision as of 23:33, 17 October 2014
XOR Gate
Model
After binding to DNA, integrases can flip the fragment and thus compute the output of the XOR logic gate.
XOR Logic Gate
We consider a binary exclusive or (XOR) logic gate, with two inputs and one output.
Biological Principles
The fragment integrases can flip is a terminator. Thus, the terminator can either be on or off.
- Ton: terminator is on, transcription is blocked.
- Toff: terminator is off, transcription is active. It corresponds to one flipping of the terminator.
In our design, we are interested in a double flipping. That is to say that two pairs of binding sites surrounds the fragment to be flipped. One pair of binding sites can be bound by DBxb1 and the other one by ΦC31.
The terminator can be flipped once if either DBxb1 or ΦC31 is present. The state Toff can be reached via two possible transitions. We further decompose it into two different states: ToffBxb1(flipping due to presence of Bxb1) and ToffΦC31(flipping due to presence of ΦC31).
Flipping by integrases is irreversible. The initial state, in which the terminator is on, is different from the state after two switches. From this last state, no further evolution of the system is possible. Therefore, we decompose the Ton into two different states: Ton,i(initial state of the system, no flipping) and Ton,f(final state of the system after two flips).
XOR biologic gate
Other Chemical Species
| Name | Description |
|---|---|
| mRNAGFP | mRNA for Green fluorescent protein which is produced when the cells are ON. |
| GFP | Green fluorescent protein which is produced when the cells are ON. |
| mRNALuxI | mRNA for LuxI which is produced when the cells are ON. |
| LuxI | Enzyme catalysing the production of LuxAHL from SAM and ACP. |
| mRNALasI | mRNA for LasI which is produced when the cell are ON. |
| LasI | Enzyme catalysing the production of LasAHL from SAM and ACP. |
Reactions
The following reactions are valid for the strain producing LasAHL as output (It corresponds to the blue cells here).
To have the equivalent for the strain producing LuxAHL as output, it suffices to replace every occurence of LasI by LuxI.
Transfer Function
Determistic Differential Equations
We modeled the XOR gate module deterministically. Thus, we considered a continuous approximation of variables, like the number of integrases-DNA binding sites or the number of terminator. We wrote them as concentration. We do not take the species LasI and mRNALasI into account because they are only produced by the XOR biologic gate and GFP is another product of this biologic gate that can be read out.
$$\begin{align*}
\frac{d[T_{on,i}]}{dt}&= -k_{ToffBxb1}[T_{on,i}][SA_{Bxb1}]^2 -k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 \\
\frac{d[T_{offBxb1}]}{dt}&=k_{ToffBxb1} [T_{on,i}][SA_{Bxb1}]^2 - k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2\\
\frac{d[T_{off\phi C31}]}{dt}&=k_{Toff\phi C31} [T_{on,i}][SA_{\phi C31}]^2 - k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\
\frac{d[T_{on,f}]}{dt}&= k_{-ToffBxb1} [T_{offBxb1}] [SA_{\phi C31}]^2 + k_{-Toff\phi C31} [T_{offBxb1}] [SA_{Bxb1}]^2\\
\frac{d[mRNA_{GFP}]}{dt}&= k_{mRNA_{GFP}} (\frac{[T_{offBxb1}]}{\theta + [T_{offBxb1}]} + \frac{[T_{off\phi C31}]}{\theta + [T_{off\phi C31}]}) - d_{mRNA_{GFP}}[mRNA_{GFP}]\\
\frac{d[GFP]}{dt}&= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP]\\
\end{align*}$$
As there is a strong codon bias in both integrases' seuquences [14], the flipping parameters were assumed such that they would not be a rate limiting step. (see the parameter pages)
Deterministic simulation
At steady state, the transfer function obtained by simulation is shown on the next figure. It is remarkable to see that even a little amount of one integrase is sufficient to switch the XOR gate on.
 "
"