Chemotaxis

Motivation

To stay true to its title 'pathogen-hunting microbe', BaKillus should ideally be able to swim towards its prey via chemotaxis. However, the ability to react to an AIP- or CSP-gradient requires the introduction of a chimeric receptor into Bacillus subtilis. Chemotaxis receptors are quite complex and can, for example, take different methylation states to allow for attenuation of the chemotactic response. This complexity puts the construction of a custom receptor beyond the scope of an iGEM project.

To evaluate how a hypothetical chemotactic BaKillis would act in an experimental setting, we developed a model to simulate the movement of chemotactic hunters in response to an attractant gradient produced by a growing colony of prey bacteria.

Overview

Our multi-scale hybrid model essentially consists of 3 components: growth of prey bacteria (algebraic model), diffusion of attractant molecules (spatial partial differential equation) and chemotactic behavior of the hunter bacteria (stochastic spatial agent model coupled to differential equations for internal state with a stochastic driving force). All these processes take place in a defined geometric space (representing, for example, a microfluidic device). The experimental scenario we wish to capture in our model is the following: a colony of prey bacteria is spotted onto the arena, growing in place and producing attractant molecules. A fixed population of hunter bacteria is placed into the arena as well. Their reaction (biased movement) to the building attractant gradient is what we seek to observe.

Growth of prey

The prey bacteria will grow on a population level, according to a logistic growth curve with explicit solutions (ref!):

\[ y = ln \frac{N}{N_0} = \frac{A}{1 + e^{\frac{4\mu_m}{A} (\lambda - t) + 2}}\]

Here, \(N_0\) is the population size at \(t = 0\), \(A = ln \frac{N_\infty}{N_0}\) is the asymptote, \(\mu_m\) is the growth rate and \(\lambda\) the duration of the lag-phase.

Diffusion of attractants

The concentration of attractant molecules (\(c\)) in space changes according to a partial differential equation comprising diffusion, degradation and production by the prey bacteria.

\[ \frac{\partial c}{\partial t} = D\Delta c + p c_{prey} - a c\]

\(D\) is the diffusion coefficient, \(a\) is the degradation rate, \(p\) the rate of production and \(c_{prey}\) the concentration of prey/producer bacteria.

Chemotaxis

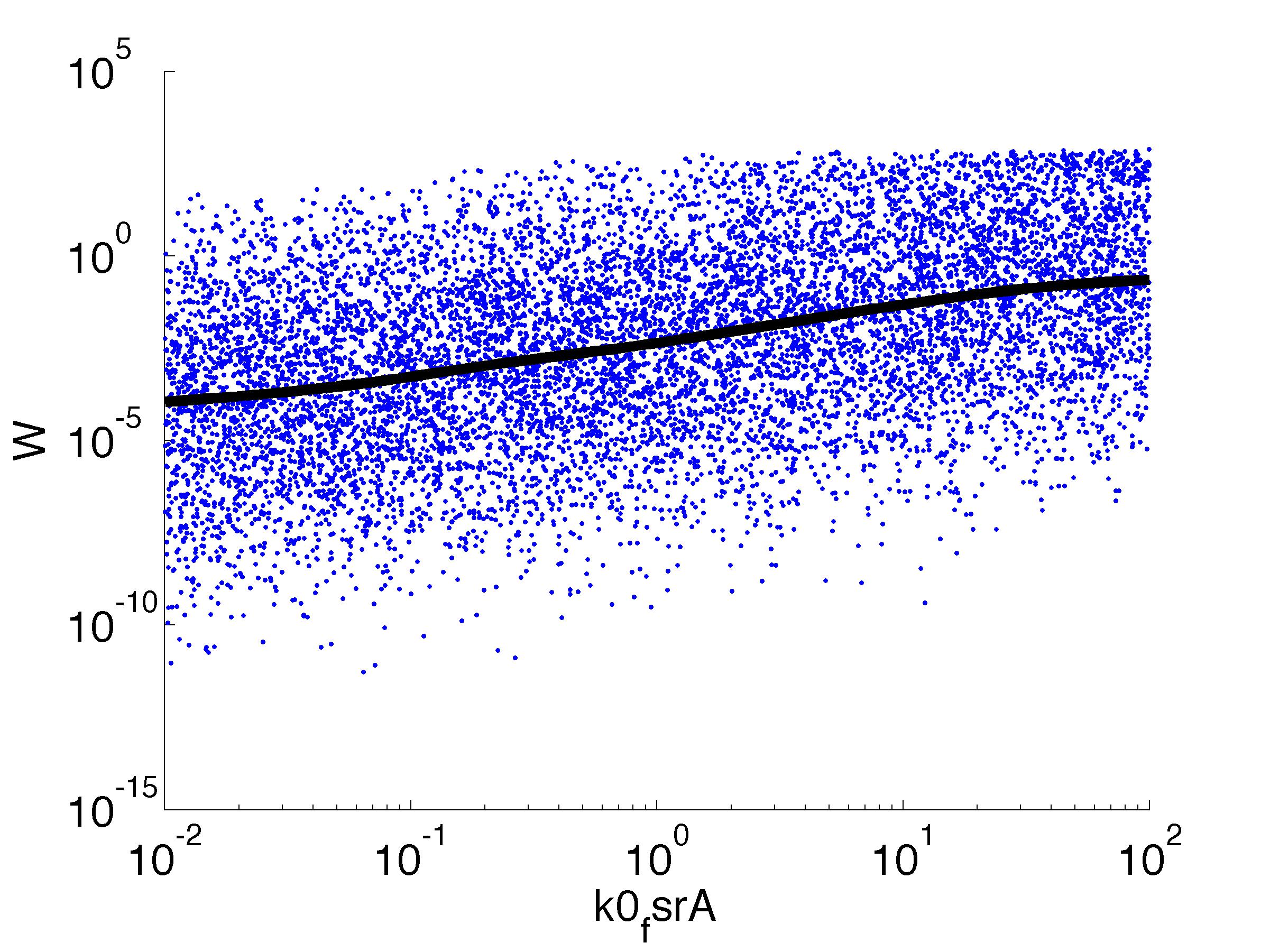
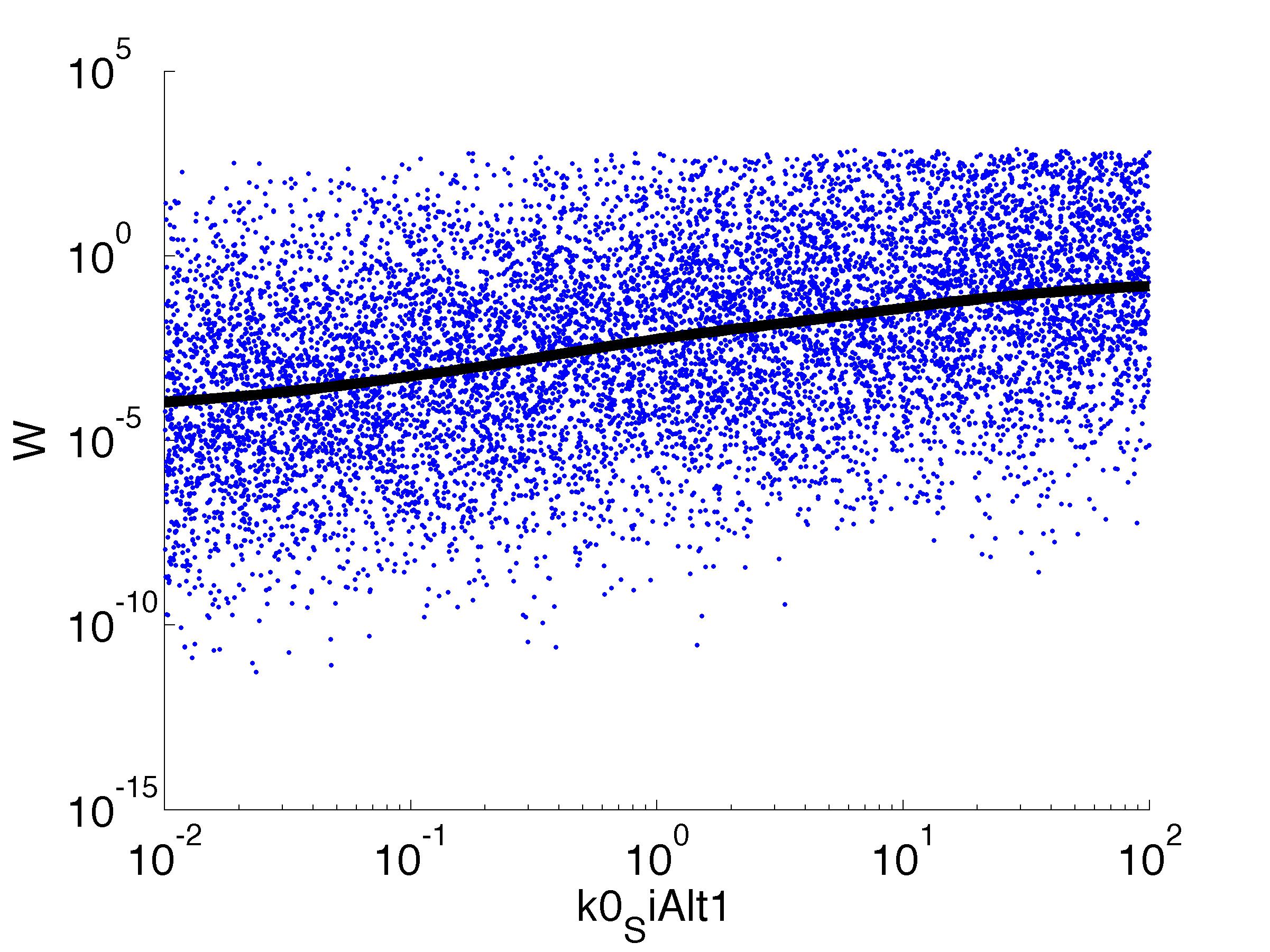
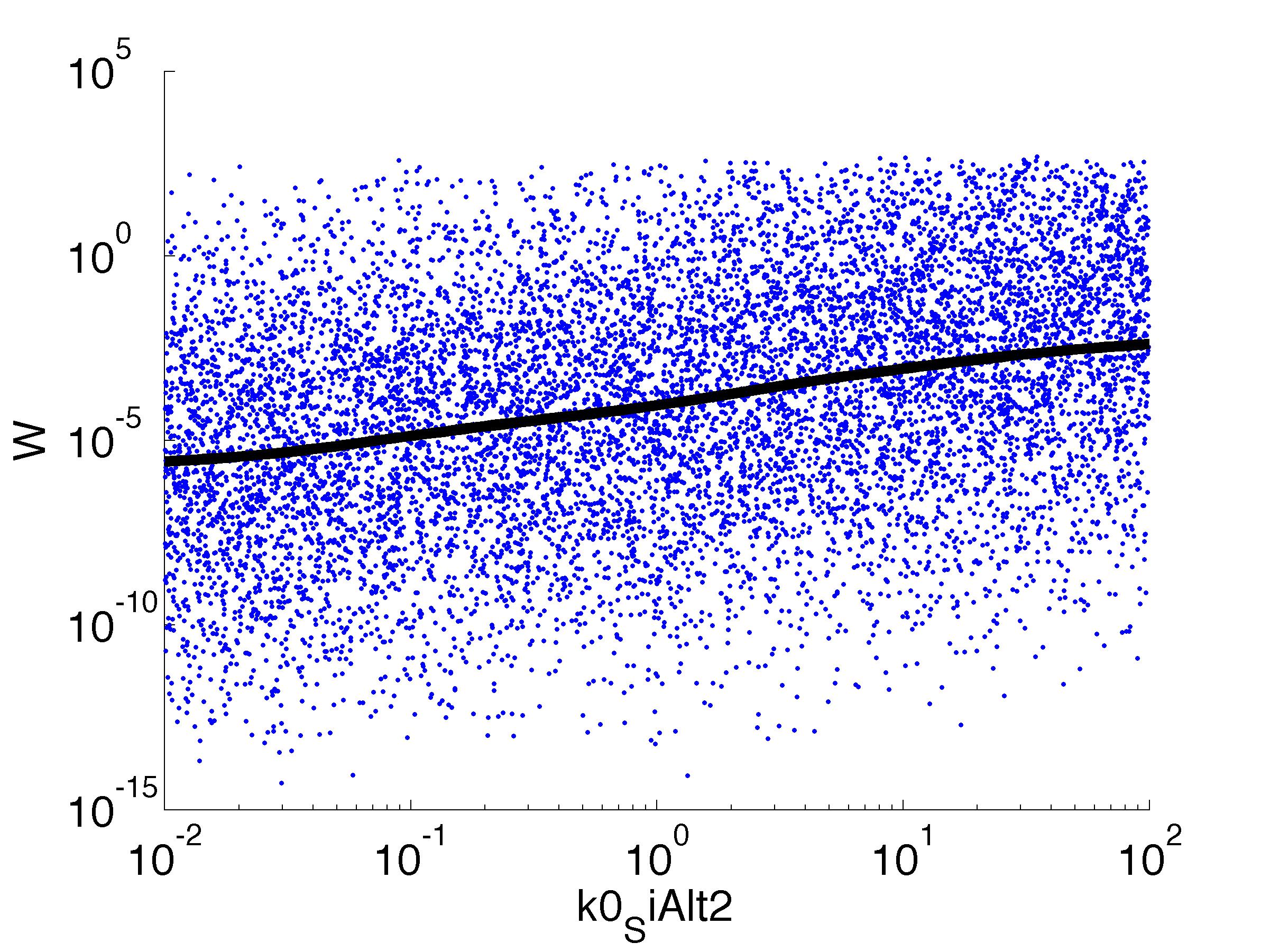
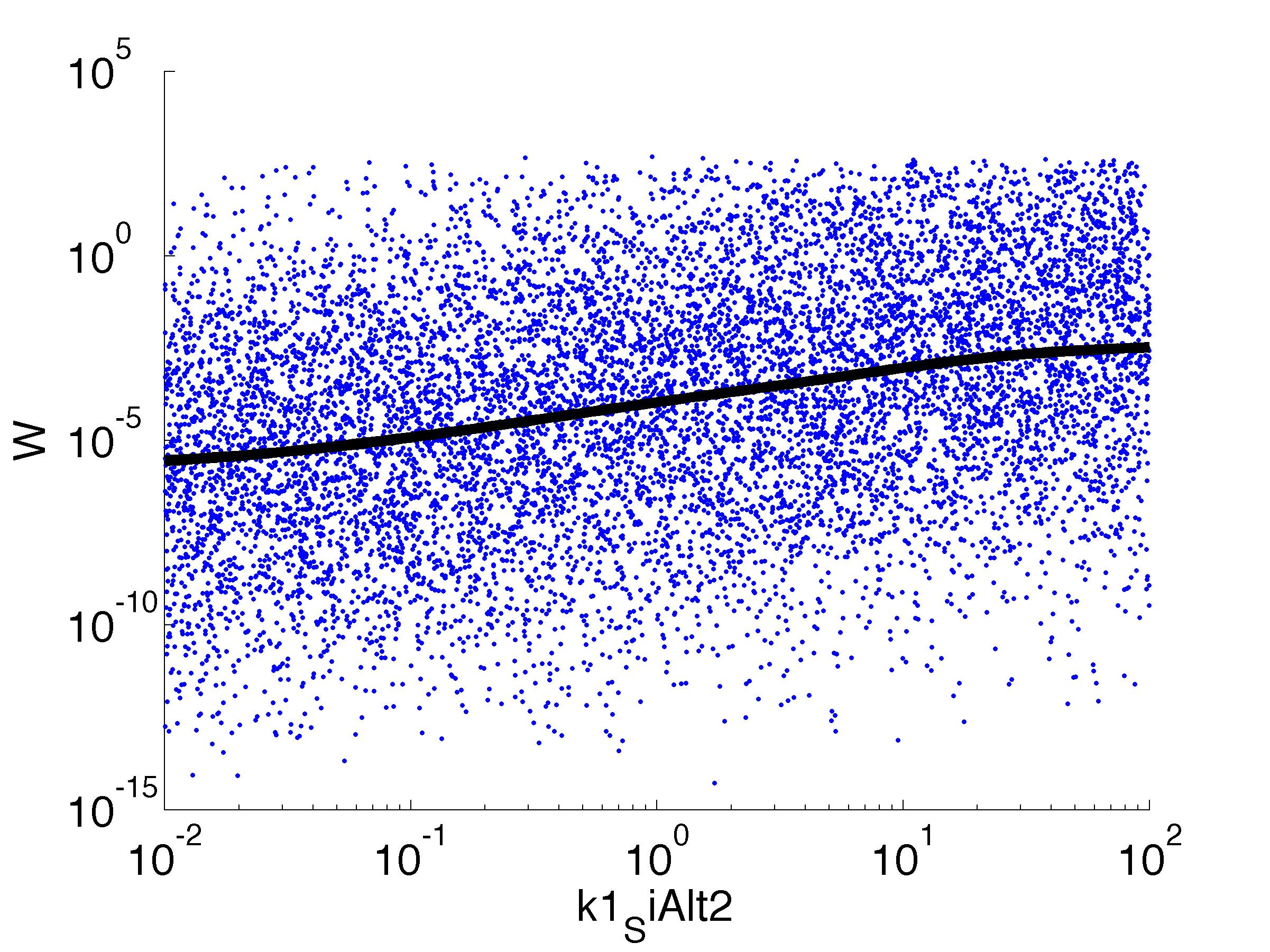
The chemotaxis of the hunter bacteria (BaKillus) is represented by an agent-based model adapted from [Matthäus ref]. Each bacterium has its own methylation and phosphorylation states of the chemotactic pathway which change according to a system of ordinary differential equations in response to attractant concentrations. In a classical 2-state model of bacterial chemotaxis, each bacterium will be in either running or tumbling state at each time point. In a running step, bacteria will swim forward in a straight line whereas in a tumbling step, they will change their direction by a random angle picked from a gamma distribution.

It should be noted that the model used here actually describes chemotaxis of E. coli. While the wiring of the chemotaxis pathway differs slightly, the same behavior is expected for B. subtilis . Therefore, we opted for the use of the better studied E. coli-model.

Implementation

We implemented the model in C++, making extensive use of the Boost libraries for numerical integration, among other things. In addition, we wrote gateway routines to allow handling of the model from a MATLAB script. This way, parameters can easily be changed and results can be visualized using the plotting functionality of MATLAB.

Initially, the arena in which chemotaxis should take place is defined as a polygon. An equally spaced 2-dimensional grid covering the polygon is created to store concentrations of prey bacteria and attractant molecules (fig. x). The area in which prey bacteria grow (a 'colony') is defined as a rectangle and their initial concentration is set.

[scheme of grid]

A desired number of virtual hunter bacteria are created at set spacial coordinates. Initially, these bacteria have a random orientation and their chemotactic pathway is inactive (methylation and phosphorylation levels are zero).

The model is then updated by defined time steps until a desired end time is reached.

At each time step, the number of prey bacteria in the colony is updated according to their logistic growth curve. The concentration of attractant molecules changes according to the diffusion equation (see above). The Laplacian is discretized on the grid using a standard 5-point stencil (pseudocode??).

In each time step, the bacteria will update their chemotactic pathway (according to the system of differential equations) in response to the attractant concentration at their location (the mean of the nonnegative concentrations at the neighboring 4 grid nodes). Each bacterium will then swim forward (run) or change its orientation (tumble) dependent on the phosphorylation level of CheY.

Results & Discussion