Team:ETH Zurich/modeling/int
From 2014.igem.org
m (→Characterization: KDBxb1) |
m (→Data) |
||
| Line 216: | Line 216: | ||
[[File:ETH Zurich Bonnet S4.jpg|center|800px|thumb|Transfer function from aTc to Bxb1. The experimental data corresponds to the points. They fitted this data with their own model. Supplementary figure S4 of Bonnet's paper ''Amplifying Genetic Logic Gates''<sup>[[Team:ETH_Zurich/project/references|[9]]]</sup>]] | [[File:ETH Zurich Bonnet S4.jpg|center|800px|thumb|Transfer function from aTc to Bxb1. The experimental data corresponds to the points. They fitted this data with their own model. Supplementary figure S4 of Bonnet's paper ''Amplifying Genetic Logic Gates''<sup>[[Team:ETH_Zurich/project/references|[9]]]</sup>]] | ||
| - | We do the same modeling steps, as for the [https://2014.igem.org/Team:ETH_Zurich/modeling/int#Characterization:_KSABxb1 previous characterization].Thus, we obtain the following set of differential equations: | + | We do the same modeling steps, as for the [https://2014.igem.org/Team:ETH_Zurich/modeling/int#Characterization:_KSABxb1 previous characterization].Thus, we obtain the following set of differential equations:$$\begin{align*} |
| - | + | ||
| - | $$\begin{align*} | + | |
\frac{d[Bxb1]}{dt} &= a_{}*(A_L + B_L * \frac{[aTc]^n}{[aTc]^n+K_L^n})- 2 k_{DBxb1}*[Bxb1]^2 + 2k_{-DBxb1}*[DBxb1] - d_{Bxb1}*[Bxb1] \\ | \frac{d[Bxb1]}{dt} &= a_{}*(A_L + B_L * \frac{[aTc]^n}{[aTc]^n+K_L^n})- 2 k_{DBxb1}*[Bxb1]^2 + 2k_{-DBxb1}*[DBxb1] - d_{Bxb1}*[Bxb1] \\ | ||
\frac{d[DBxb1]}{dt} &= k_{DBxb1}*[Bxb1]^2 - k_{-DBxb1}*[DBxb1] - k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] + k_{-SABxb1}*[SA_{Bxb1}] - d_{DBxb1}*[DBxb1] \\ | \frac{d[DBxb1]}{dt} &= k_{DBxb1}*[Bxb1]^2 - k_{-DBxb1}*[DBxb1] - k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] + k_{-SABxb1}*[SA_{Bxb1}] - d_{DBxb1}*[DBxb1] \\ | ||
Revision as of 15:00, 12 October 2014
Integrases
Model
In our design, integrases compute the output of the logic gates. Integrases allow to flip one fragment of DNA. The model we developped is described here.
Chemical Species
| Name | Description |
|---|---|
| Bxb1 | Serine integrase that can fold into two conformations called Bxb1a and Bxb1b. Even if those conformations have the same sequence of amino acids, their tertiary structure is different. As it is experimentally difficult to differentiate these two conformations, we chose to to use a common notation for both conformations. |
| ΦC31 | Serine integrase that can fold into two conformations called ΦC31a and ΦC31b. Similarly to Bxb1, we chose to use a common notation for both conformations. |
| DBxb1 | Dimer of Bxb1. Bxb1a (respectively Bxb1b) forms a dimer DBxb1a (respectively DBxb1b). To be coherent, dimers are not differentiated depending on their spatial configuration. |
| DΦC31 | Dimer of ΦC31. ΦC31a (respectively ΦC31b) forms a dimer DΦC31a (respectively DΦC31b). The different spatial configuration are not taken into account. |
Modeling DNA-binding sites
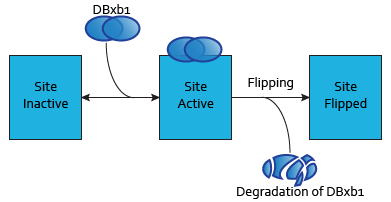
Each dimer of integrases can specifically bind to a DNA binding site. As the flipping is irreversible, these DNA binding sites can be three possible states:
- SIIntegraseName: inactive DNA binding site. No dimer is bound to this site, which has never been flipped.
- SAIntegraseName: active DNA binding site. A dimer is to this site.
- SFIntegraseName: flipped DNA binding site. This DNA binding site has been used by a flipping.
Reactions
- For Bxb1
$$ \begin{align} Bxb1 + Bxb1 &\leftrightarrow DBxb1 \\ DBxb1 + SI_{Bxb1} & \leftrightarrow SA_{Bxb1}\\ Bxb1 &\rightarrow \\ DBxb1 &\rightarrow \end{align}$$
- For ΦC31
\begin{align} \phi C31 + \phi C31 &\leftrightarrow D\phi C 31 \\ D\phi C 31 + SI_{\phi C31} & \leftrightarrow SA_{\phi C31}\\ \phi C31 &\rightarrow \\ D\phi C31 &\rightarrow \end{align}
Differential Equations
Applying mass action kinetic laws, we obtain the following set of differential equations for Bxb1.
$$\frac{d[Bxb1]}{dt}=-2 k_{DBxb1}[Bxb1]^2+ 2 k_{-DBxb1}[DBxb1]-d_{Bxb1}[Bxb1]$$
$$\frac{d[DBxb1]}{dt}=-k_{SABxb1}[DBxb1][SI_{Bxb1}]+k_{-SABxb1}[SA_{Bxb1}]+k_{DBxb1}[Bxb1]^2-k_{-DBxb1}[DBxb1]-d_{DBxb1}[DBxb1]$$
$$\frac{d[SA_{Bxb1}]}{dt}=k_{SABxb1}[DBxb1][SI_{Bxb1}]-k_{-SABxb1}[SA_{Bxb1}]$$
Replacing every occurence of Bxb1 by ΦC31 gives the set of differential equations for ΦC31.
State of the Art
| Name | Description | Status from literature | Status after characterization |
|---|---|---|---|
| kDBxb1 | Dimerization rate of Bxb1 | Unknown | Fitted |
| k-DBxb1 | Dissociation rate of DBxb1 | Unknown | Fitted |
| kSABxb1 | Rate of formation of SABxb1 from DBxb1 and SIBxb1 | Unknown | Fitted |
| k-SABxb1 | Dissociation rate of SABxb1 | Unknown | Fitted |
| dBxb1 | Degradation rate of Bxb1 | Unknown | Assumed |
| dDBxb1 | Degradation rate of DBxb1 | Unknown | Assumed |
Replacing every occurence of Bxb1 by ΦC31 gives the set of parameters for ΦC31. The same status can be applied to those parameters.
Even if degradation rates were not determined specifically for the serine integrases and their dimerized form, degradation rates of proteins in E. coli are available. To characterize integrases behavior, we focus on finding the parameters for dimerization and DNA-binding.
Characterization: KSABxb1
Data
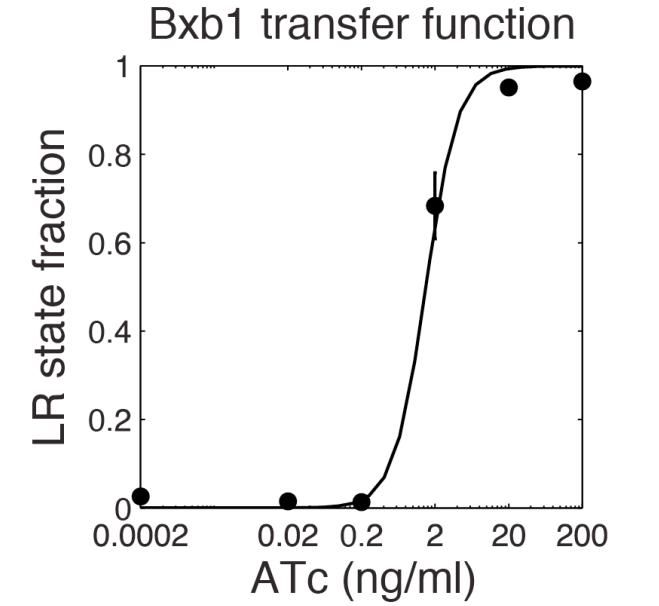
The parameter fitting is based on Bonnet's paper[9]. Their experimental setup is different from ours. However, they experimentally retrieve a transfer function between aTc and Bxb1 switching rate. Here is the figure of interest in our case.
To use their experimental data, we have to model their induction mechanism using aTc. We use a simplify version of it proposed by the 2013 iGEM team UCSF. They modeled the induction with aTc as a leaky Hill function. In the following table are the set of parameters introduced to model induction.
| Name | Value | Description | Reference |
|---|---|---|---|
| AL | 8.904 mRNA min-1 | Basal expression level of tet promoter | [2013 iGEM team UCSF] |
| BL | 443.7 mRNA min-1 | Maximal expresion level of tet promoter | [2013 iGEM team UCSF] |
| n | 2.551 (no units) | Hill exponent | [2013 iGEM team UCSF] |
| Km | 11.45 µmoles | Half-maximal effective concentration of aTc | [2013 iGEM team UCSF] |
| kmRNABxb1 | Unknown | Translation rate of Bxb1 |
We obtain the following set of differential equations:
$$\begin{align*} \frac{d[Bxb1]}{dt} &= k_{mRNA_{Bxb1}}*(A_L + B_L * \frac{[aTc]^n}{[aTc]^n+K_L^n})- 2 k_{DBxb1}*[Bxb1]^2 + 2k_{-DBxb1}*[DBxb1] - d_{Bxb1}*[Bxb1] \\ \frac{d[DBxb1]}{dt} &= k_{DBxb1}*[Bxb1]^2 - k_{-DBxb1}*[DBxb1] - k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] + k_{-SABxb1}*[SA_{Bxb1}] - d_{DBxb1}*[DBxb1] \\ \frac{d[SA_{Bxb1}]}{dt} &= k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] - k_{-SABxb1}*[SA_{Bxb1}] \end{align*}$$
Assumptions
- Assumption A
- The back-reaction from DBxb1 binding to site inactive is considered to be negligible, compared to the flipping rate. That is to say that once a site is active, it can only be flipped. Thus, an active site would only be a transitional state in our whole cell model. As the flipping is not modeled in our integrase subsystem, active sites are not transformed into flipped sites at the end of the information pipeline. Thus, we consider that we can express the switching rate given active site concentration.
- Assumption B
- As switching needs two active sites to be effective (for more information on flipping, check the XOR gate page), the switching rate is approximated to: $${(\frac{SA_{Bxb1}}{S_{TOT}})}^2$$ This approximation is understated by statistical considerations.
- Assumption C
- Given the normalization of the paper, basal rate of production of Bxb1 is not taken into account. Thus, we consider that $$A_L = 0$$
- Assumption E
- The activation by aTc is assumed to be dominant over degradation of Bxb1 and dimerization of Bxb1. It is supposed to be valid on the range of aTc concentration considered.$$\frac{k_{mRNA_{Bxb1}}*(A_L + B_L * \frac{[aTc]^n}{[aTc]^n+K_L^n})}{d_{Bxb1}K_{DBxb1}} >> 1$$ with $$K_{DBxb1} = \frac{k_{-DBxb1} + d_{DBxb1}}{k_{DBxb1}}$$
Parameter fitting
We consider the system at steady-state. After derivation, the following explicit equation can be retrieved:
$$[SR]_{qss} = {(\frac{B_{L} * [aTc]^{n}}{ \lambda_1 K_L^{n} + (B_{L} +\lambda_1) [aTc]^{n}})}^2$$
where
$$\lambda_1 = \frac{2*d_{Bxb1}*K_{SABxb1}}{k_{mRNA_{Bxb1}}} ; K_{SABxb1} = \frac{k_{-SABxb1}}{k_{SABxb1}}$$
Range of validity of the assumptions
Characterization: KDBxb1
Data
The parameter fitting is based on Bonnet's paper[9]. Their experimental setup is different from ours. However, they experimentally retrieve a transfer function between aTc and Bxb1 switching rate. Here is the figure of interest in our case.

We do the same modeling steps, as for the previous characterization.Thus, we obtain the following set of differential equations:$$\begin{align*} \frac{d[Bxb1]}{dt} &= a_{}*(A_L + B_L * \frac{[aTc]^n}{[aTc]^n+K_L^n})- 2 k_{DBxb1}*[Bxb1]^2 + 2k_{-DBxb1}*[DBxb1] - d_{Bxb1}*[Bxb1] \\ \frac{d[DBxb1]}{dt} &= k_{DBxb1}*[Bxb1]^2 - k_{-DBxb1}*[DBxb1] - k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] + k_{-SABxb1}*[SA_{Bxb1}] - d_{DBxb1}*[DBxb1] \\ \frac{d[SA_{Bxb1}]}{dt} &= k_{SABxb1}*[DBxb1]*[SI_{Bxb1}] - k_{-SABxb1}*[SA_{Bxb1}] \end{align*}$$
Assumptions
- Assumption A
- The back-reaction from DBxb1 binding to site inactive is considered to be negligible, compared to the flipping rate. That is to say that once a site is active, it can only be flipped. Thus, an active site would only be a transitional state in our whole cell model. As the flipping is not modeled in our integrase subsystem, active sites are not transformed into flipped sites at the end of the information pipeline. Thus, we consider that we can express the switching rate given active site concentration.
- Assumption B
- As switching needs two active sites to be effective (for more information on flipping, check the XOR gate page), the switching rate is approximated to: $${(\frac{SA_{Bxb1}}{S_{TOT}})}^2$$ This approximation is understated by statistical considerations.
- Assumption F
- We neglect the degradation rate of DBxb1, dDBxb1, with respect to the dimerization reaction.
Parameter fitting
Range of validity of the assumptions
 "
"