"

From 2014.igem.org

You might be wondering where these patterns on snea snail shells come from. What if they would come from a simple rule, followed by all cells on the shell ?

   
    
    
    
    
    
    
    
    
    
    
    
    
Automaton Explorer
    

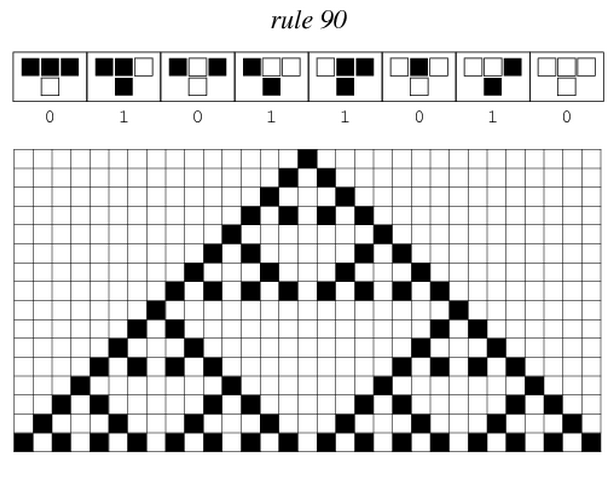
    rule: 30
    
    start: 
    point
    
    random
    
    

    
    
From MathWorld:
    "A cellular automaton is a collection of 'colored' cells on a grid of
    specified shape that evolves through a number of discrete time steps
    according to a set of rules based on the states of neighboring cells." This
    example explores binary, nearest-neighbor, one-dimensional automata, of
    which there are 256 (28) possible rules. The eight possible
    outcomes for the current rule are shown across the top; click to toggle the
    selected bit.
    
    

Gitorious

   Activities
   Projects
   Teams
   About

<script>

   /** Depends on globals: rule, w, h, mode. */
   function cell() {
   var d = pv.range(h).map(function() {
   return pv.range(w).map(function() { return 0; });
   }),
   r = pv.range(8).map(function(i) {
   return rule >> i & 1;
   });
   if (start == "point") {
   d[0][w >> 1] = 1;
   } else {
   for (var x = 0; x < w; x++) {
   d[0][x] = cell.random(x);
   }
   }
   for (var y = 1; y < h; y++) {
   var p = d[y - 1], c = d[y];
   for (var x = 0; x < w; x++) {
   c[x] = r[p[x - 1] << 2 | p[x] << 1 | p[x + 1]];
   }
   }
   return d;
   }
   cell.$random = {};
   /** Caches random output to make exploration deterministic. */
   cell.random = function(i) {
   return i in cell.$random ? cell.$random[i]
   : (cell.$random[i] = Math.random() < .5 ? 0 : 1);
   };

</script>