Team:ETH Zurich/modeling/diffmodel
From 2014.igem.org
Diffusion model
Model
The main experiment for investigating diffusion is a propagation of the whole pattern through the chip via the quorum sensing module only. We have used beads containing cells which are able to sense luxAHL, produce GFP when they sense it, and amplify the signal for the next row. The combination of the quorum sensing module with diffusion enables to check that cells will amplify the signal enough from one row to the next one, and to check what would be the time scale of the pattern formation. We used a reaction-diffusion model to combine quorum sensing reactions and diffusion.
Geometry and boundary conditions
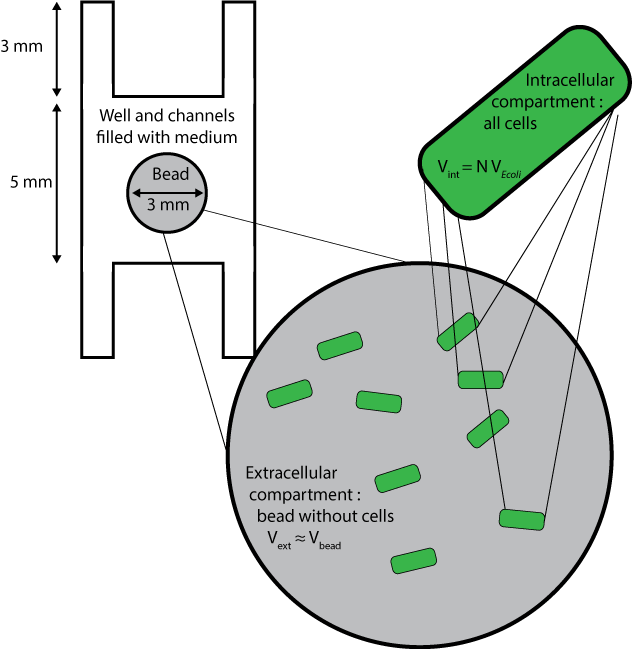
Three different compartments are considered :
- The wells and channels, which are filled with liquid medium and where extracellular AHL only can diffuse, with its diffusion coefficient D, and degrade with the degradation rate dAHLext.
- The beads without the cells inside them, whose volumes are approximated to the volume of beads themselves, and where extracellular AHL only can degrade and diffuse, with a slighty lower diffusion coefficient 0.9*D.
- The cells, which are considered altogether as one compartment, and which contains all species except extracellular AHL.
In order to fulfill these conditions in Comsol Multiphysics, the cells are not drawn but instead, beads are considered as compartments with a certain density of cells. Rates of diffusion through the membrane are added as reaction rates and intracellular species are contained in beads via a Newmann's boundary condition applied to the surface of the beads, that is : $$ \nabla C . \textbf{n} =0$$ $$\text{for all species except extracellular AHL}$$ $$\text{for every vector n normal to the surface of a bead}$$
Species and reactions
| Name | Description |
|---|---|
| AHLint | LuxAHL inside cells |
| AHLext | LuxAHL outside cells |
| LuxR | Constitutively expressed regulator protein that can bind LuxAHL and stimulate transcription of GFP. |
| RLux | LuxR and LuxAHL complex which can dimerize. |
| mRNAGFP | mRNA for Green fluorescent protein which is produced when the cells are ON. |
| GFP | Green fluorescent protein which is produced when the cells are ON. |
| mRNALuxI | mRNA for LuxI which is produced when the cells are ON. |
| LuxI | Enzyme catalysing the production of LuxAHL from SAM and ACP. |
The beads are the compartments containing the cells. The number of cells per bead is called N. The fraction of volume occupied by cells to total bead volume is $$\frac{V_{\text{internal to cells}}}{V_{\text{bead}}}=N \ \ V_{E. coli}$$
$$ \begin{align} \emptyset&\rightarrow LuxR \\ LuxAHLext & \leftrightarrow LuxAHLint\\ LuxAHLint+LuxR & \leftrightarrow RLux\\ RLux+RLux &\leftrightarrow DRLux\\ DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ P_{luxON}&\rightarrow P_{luxON}+mRNA_{GFP}\\ mRNA_{GFP}&\rightarrow GFP \end{align}$$
Equations
Deriving diffusion rates
We are using a reaction-diffusion model, which means that for internal and external AHL species which diffuse, we have to include a diffusion rate in addition to reaction rates from the quorum sensing module :
$$\frac{d[AHL]}{dt}=\mathcal{Diff}(AHL)+\mathcal{R}(AHL)$$
According to Fick's law of diffusion, the flow of AHL Φ(AHLint) (number of molecules per second) from the bead into the cells and the flow of AHL Φ (AHLext) from cells into the bead are
$$\Phi(AHL_{int}) = N \sigma \mathcal{A} ([AHL_{ext}]-[AHL_{int}]) \\ \Phi(AHL_{ext}) = N \sigma \mathcal{A} ([AHL_{int}]-[AHL_{ext}])$$
$$\text{where }\sigma \text { is the membrane permeability}$$
$$\mathcal{A} \text{ is the area of the membrane}$$
$$N \text{ is the number of cells per bead.}$$
Thus the diffusion rate of internal AHL (concentration per second) is :
$$ Diff(AHL_{int})=\frac{N \sigma \mathcal{A}}{V_{int}} ([AHL_{ext}]-[AHL_{int}])=D_m ([AHL_{ext}-[AHL_{int}]) $$
$$\text{where } V_{int} \text{ is the total volume of all cells}$$
$$D_m \text{ is a lumped coefficient for diffusion through the membrane}$$
and the diffusion rate of external AHL is $$Diff(AHL_{ext})=\frac{N \sigma \mathcal{A}}{V_{bead}} ([AHL_{ext}]-[AHL_{int}])= \frac{N V_{E.coli}}{V_{bead}}D_m([AHL_{ext}]-[AHL_{int}]) = N \alpha D_m([AHL_{ext}]-[AHL_{int}]) $$
$$ \text{where } \alpha = \frac{V_{E.coli}}{V_{bead}}$$ $$V_{E.coli} \text{ is the volume of one cell }$$ $$V_{bead}\text{ is the volume of one bead.} $$
Modeling growth
We have used a function of logistic growth function for the number of cells: $$ \frac{N_0 N_m e^{rt}}{N_m+N_0(e^{rt}-1)} $$ $$\text{where } N_0 \text{ is the initial number of cells per bead} $$ $$N_m \text{ is the maximum number of cells per bead}$$ $$r \text{ is the growth rate }$$
Set of equations used
$$ \begin{align*} \frac{d[AHLext]}{dt} &= \rho \ V_{E. coli}\ D_m \ (AHL_{int}-AHL_{ext}) -d_{AHLext}[AHL_{ext}]\\ \frac{d[AHLint]}{dt} &= Dm (AHL_{ext}-AHL_{int}) + k_{-RLux}[R_{Lux}]-k_{RLux}[LuxAHL_{int}][LuxR]-d_{AHLint}[AHL_{int}]\\ \frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[AHL_{int}][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ \frac{d[RLux]}{dt} &= k_{RLux}[AHL_{int}][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ \frac{d[mRNA_{GFP}]}{dt} &= \frac{k_{mRNA_{GFP}}[RLux]^2}{K_{mLux}^2 + [RLux]^2}- d_{mRNA_{GFP}} [mRNA_{GFP}]\\ \frac{d[GFP]}{dt} &= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP]\\ \end{align*} $$
Initial conditions
Parameter estimation
The initial number of beads is 10 million. A master thesis showed that in picoliter beads, the growth rate of cells is
Results
Pattern developing
The developing pattern shows that every row senses the signal coming from above, amplifies it and is capable to send a signal to the next row, which is high enough to enable propagation until the bottom of the grid. We can see that the dynamics of the model are very well fitted to experimental conditions.
The background in our experimental setup is very high and this is high we see actual fluorescence appear only after 11 hours. In order to account for this, we also set up a background in the simulated pattern by adjusting the scale.
Video --------------------
Dynamics by row
Here you can see the quorum sensing mechanism happening in several rows at different moments.
 "
"