Matt says:

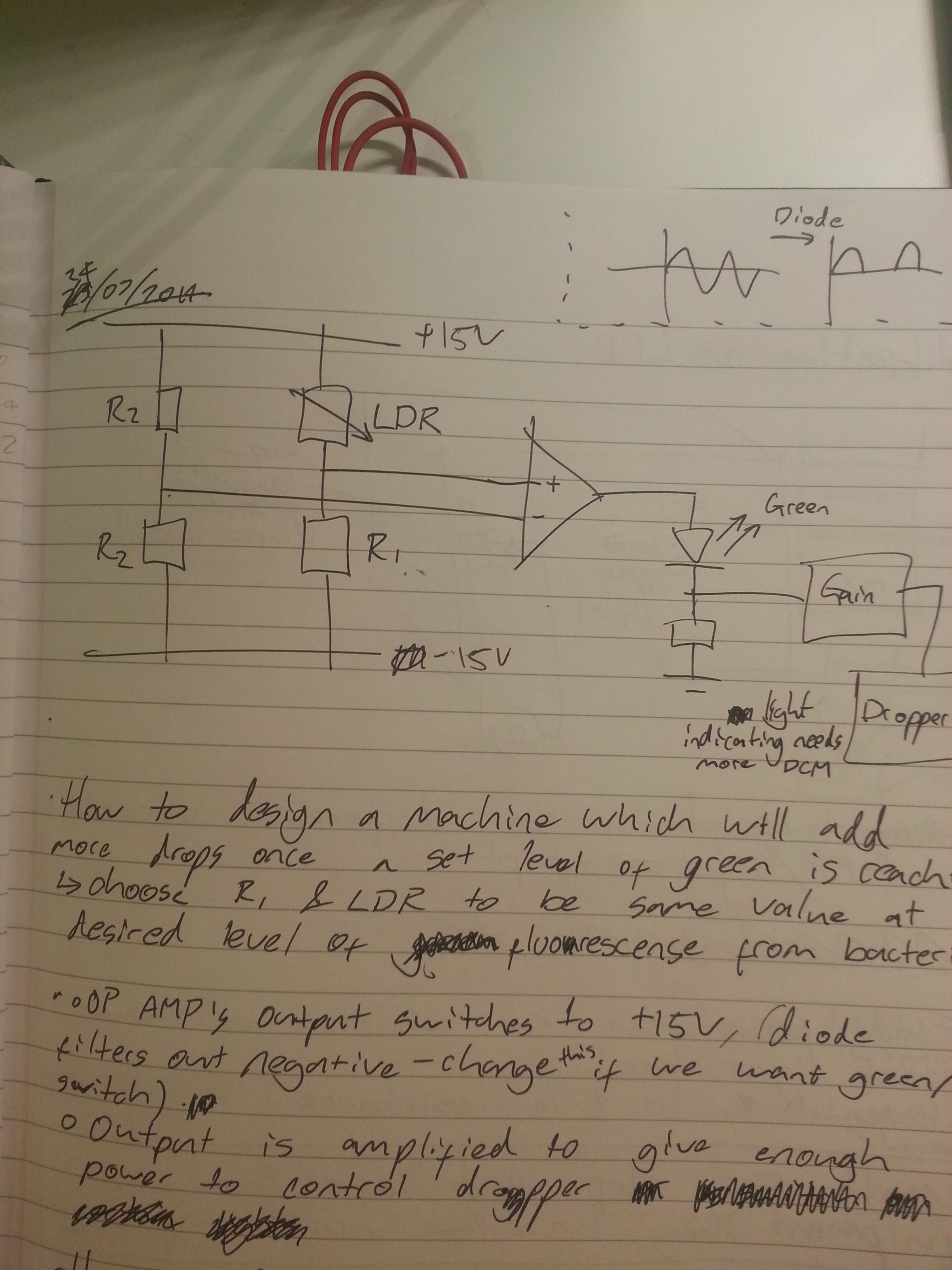
Spent this morning learning how to produce 2D/3D graphs on matlab. In the afternoon, we thought about some ideas for having a digital (and continuous) test for when the DCM had been used up to a defined level, using comparators and light dependent resistors.

Above is a basic design for a circuit which will have a glowing (Green) LED when the fluorescent bacteria reach a certain light level (level to be found later). Once the light level is found, i will record the value of the LDR's resistance at this level, i will set R1 to this value so that the comparator will switch at this point. Depending on the design for the container this could then possibly be linked to a digital dispencer of DCM/Nutrients for bacteria.

Oliver says:

The effect of changing the activation and degradation rate of the sfGFP protein.

The effect of changing the degradation rate of the sfGFP protein.

Oliver says:

Had a long chat with Fran, George, Ciaran and Glen this morning about the surface plot, we established that if the system behaves as the model predicts it will be very beneficial. This is because it provides a sharp cut off when the amount of DCM gets low, this is exactly what is needed as we're designing an on/off biosensor.

We established that as long as the concentration of TCY stays above a certain threshold (this threshold will remain unknown until we get lab data), the response of the system isn't affected by the concentration of TCY. Therefore, in experiments and models from now on, we will be holding TCY constant while changing the concentration of DCM. In some experiments it will be a step up and a ramp down (to simulate real life as the DCM gets degraded) and in other experiments we will be using a step up and a step down in concentration of DCM to check that our biosensor is responding correctly and robustly.

I think that the model will help to cut down the number of experiments necessary by quite a lot.

I will now plot graphs of how the GFP expression will change in response to a step up and step down in DCM concentration depending on varying expression rate and degradation rate of GFP. The biochemists assure me that these two parameters are the only two that we can realistically play around with.

Also had a chat with Jack about doing surface plots that displayed the expected output of the variation in diffusivity of DCM and H2O through the polymer that he's making, depending on the thickness of the polymer and the AcCl stoichoimetry in synthesis. This polymer will coat the agarose beads that will contain the bacteria. It will be important to maintain the correct concentration of DCM inside the beads so obtaining the correct surface plot will be important.

Plated up some bacteria cultures with Phil in the evening!

Matt says:

I spent today reading up on lecture notes for modelling biochemical systems and catching up with Ollie's progress. Also qualitatively described the effect of GFP's ( or DCMA) degradation rate on its production over time as it uses up the DCM.

Oliver says:

Today I pretty much nailed the time varying 3D surface plot. It allows the user to see the variation in fluorescence over time when varying amounts of DCM and tetracycline are added. It has shown how important varying time will be when taking measurements of GFP to allow the characterization of this system.

Oliver says:

Today was spent sat at the computer writing code. Last Thursday George introduced me to a few extra levels that were involved in the real system and so would require these extra levels to be built into the model. I have been thinking about these complications over the weekend and I'm pretty sure that I was able to work out how to modify the relevant equations accordingly.

The new model that I built in the morning took into account not only the addition of Tetracycline, but also the addition of DCM to the system. This means that the model responds much more robustly and accurately to extreme circumstances, such as when either TCY or DCM is set to zero.

In the afternoon I successfully plotted the variation in the value of steady state GFP after addition of varying amounts of DCM and TCY. Next goal is to combine these to get a surface plot!

Jack says:

(Part D): A very productive day designing the bacterial containment system and overall chemical/mechanical logistics;

1 uL (agarose or agar or ... )-bacteria 'beads' will be coated with a partially permeable polymer to DCM -this is doable by exploiting the difference in polarity of DCM and H2O/HCl/things we want free movement of through the capsule-, with rate of DCM diffusion across it less than or equal to the rate of DCM breakdown. The aim is maintaining an internal capsule steady state [DCM], while enabling direct capsule exposure to high [DCM]. In our physical system, the beads will have intermediate density between water, 1.000 g/ml, and DCM, 1.325 g/ml, lying at the interface of a biphasic mixture of the two, giving our bacteria access to both components.

The DCM permeability will be controlled by the polymer type and coating thickness, while overall capsule density may be modified, if necessary, by introducing a second permeable coating of tunable density.

Solving the pH drop problem (without anion exchange diffusion dialysis/pumps):
our viable pH range is 5.5-8

1. We will have a buffer, minimising the effect of HCl production.
2. As HCl is much more soluble in water than DCM, it will be predominantly in the aqueous layer; we will replace it when it gets to {specific pH chosen, near viable limits}, shown with the appropriate pH indicator (added with the buffer and other 'biochem. compounds...' as 'powder mix')

To summarise, how it will work in practice:

1. To the graduated PTFE container with tap, add in any order, the ratios:
   
   X mL DCM : Y mL water : Z g 'powder mix'
   
2. When the aqueous layer goes {insert pH indicator colour}, empty the aqueous layer using the side-tap (run-off can be put through HCl reclamation, or neutralised e.g. by ammonia to produce ammonium chloride -important in agrochem. industry as fertilizer- or then safety poured down a sink).
3. See remaining volume of DCM layer, re-add water and 'powder mix' to maintain ratios.
4. repeat 2-3 until bottom darker, yellow (DCM) layer is gone.

The strengths of this setup are that it eliminates the need for pump and dispensing systems, so no (expensive) moving or electrical parts to go wrong, while keeping minimal user intervention. The larger the H2O/DCM vol. ratio, the slower the pH drop, so we can model & optimise this.

Next, for me, is to experiment producing agarose etc. beads by various methods, identify candidate coating materials and do kinetic calculations based on permeability data to determine required coating thicknesses, and identify coating methods (spray-coating, etc) that the bacteria will survive. Once we have our working bacteria and all data the biochemists want, I suggest making just the beads (no polymer) and seeing what they do in e.g. 10mM DCM, followed by the complete system.

Oliver says:

Sheffield meet up!

Oliver says:

Spent the morning with Jack looking at where the parameters come in. Played with the model and after speaking with George discovered that I hadn't modelled quite what the system is.

Jack says:

(Part A): Modelled the thermodynamics of solution-vapour equilibration, justifying our [DCM] approximation by calculating its deviation due to this effect.

Oliver says: - Major Breakthrough

Finished the first draft of the model, will leave it until we have real data to feed back into the system. The model is very robust and allows any user to input a large variety of parameters and scenarios that could be realistically expected in the laboratory results. The output of the model is the colour that you can expect over time (the outputs of the real system will be from a combination of mCherry and GFP).

The model reveals surprising results, including how even a small basal rate of gene expression (due to leakage of the promoters) can really change the results.

The way that I finally got the model to work was by returning to the ODE15s function in Matlab and not bothering with Laplace transforms. Information on how to use Matlab to model repressor and activator networks very easily, accurately and quickly will be uploaded to this wiki soon! If you want more details please don't hesitate to contact us.

Oliver says:

Today was difficult. It was spent trying to write Matlab code to solve the differential equations. Having already written the code successfully for an autorepressor and an autoactivator using the built in function ode15s, I thought it would be relatively easy to use similar code to model a network. However, I ran into quite a lot of problems with transferring all of the required values back and forth between the function script and the data entry script.

In the afternoon, I tried to get the model to work using Laplace transforms and more specifically Matlab's incredible computing ability at calculating the inverse laplace transform of complex functions to allow solutions to be obtained. However, this presented more problems than the ode15s function due to vector sizes and things that quite quickly got quite messy.

Help with the autorepressor/autoactivator code will be up on the wiki shortly, please don't hesitate to contact us in the meantime for more info though.

Jack says:

(Part B): day 1 modelling was spent setting up a kinetic 'map' of the tetR system as a biological repressor analogue to uncharacterised dcmR. Stochastic kinetic data was found 2 and required coefficients approximated (relative orders of magnitude) from these data sets will be fed into Ollie's ODE Model.

Oliver says:

The morning was spent with Glen and Fran (who are working on part B) discussing exactly what network of activation and repression we were trying to categorize and turning it from Snapgene files (that the Biochemists understand) into a series of possible repression and activation scenarios.

Then, it was a matter of condensing the network of seemingly complex interactions into a set of differential equations with the relevant constants. This allows the response of the system to an external known input be accurately modeled.