Team:Oxford/biosensor characterisation
From 2014.igem.org
(Difference between revisions)
MatthewBooth (Talk | contribs) |
|||
| Line 384: | Line 384: | ||
| - | Stochastic modelling uses probability theory to predict the behaviour of a system. For our project, we used it to model the expression of | + | Stochastic modelling uses probability theory to predict the behaviour of a system. For our project, we used it to model the expression of the mCherry protein from bacteria. |
<br><br> | <br><br> | ||
| - | We started with the Gillespie Algorithm, which considers the expression of | + | We started with the Gillespie Algorithm, which considers the expression of mCherry to be binary; a molecule of GFP is either expressed or degraded. Before we determined which event happened, we had to work out when the event happened. Using the random number r1 (taken from a uniform distribution between 0 and 1), we produced another random number τ, which determined the time until the next reaction. |
<br><br> | <br><br> | ||
<img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:8%; width:20%;" /> | <img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:8%; width:20%;" /> | ||
| Line 397: | Line 397: | ||
<br><br><br><br><br><br> | <br><br><br><br><br><br> | ||
| - | We modelled the probability of a molecule of | + | We modelled the probability of a molecule of mCherry being created using the Michaelis-Menten model (α1), incorporating a basal transcription rate (b1). For the degradation, we assumed a simple proportional relationship: the more mCherry you have, the more likely it is that a molecule degrades (δ1). The constant of proportionality will be a function of the intrinsic life time of the protein in the cell. We considered there to be no ATC originally, then a large step in ATC at time=50. |
<br><br> | <br><br> | ||
| - | To decide if | + | To decide if mCherry was expressed, we looked at the percentage of events which were expressions. Then we compared this to a second random number r2 (again taken from a uniform distribution from 0 to 1). If the random number was lower, then mCherry was expressed. If it was higher, then a mCherry was degraded. In this way we make a weighted random choice about whether mCherry was expressed or degraded. We only stored the time and amount of mCherry when there was a event, to save on computation time. |
<br><br> | <br><br> | ||
| Line 405: | Line 405: | ||
<br><br><br><br><br><br> | <br><br><br><br><br><br> | ||
| - | Stochastic modelling is useful because it can show us the stochastic effects which are often observed in individual bacteria. By calculating the variation of the mean of multiple | + | Stochastic modelling is useful because it can show us the stochastic effects which are often observed in individual bacteria. By calculating the variation of the mean of multiple mCherry producing bacteria, we can also work out the standard deviation. Then if we assume that the system varies with respect to the normal distribution, we can produce error bounds for the production of GFP, such that we can say that 90% of the time we can expect the production of mCherry from a single bacterium to be within these two curves. This could be useful for seeing if results are unexpected, or, if there are multiple outliers, that our model is incorrect. If we average an increasing number bacteria, then the mean curve tends towards the deterministic response. This is to be expected, as we are now looking at the system as a whole and fluctuations in the production from individual bacteria are averaged out. In terms of their use, when looking at small amounts of bacterium the stochastic model would be better, because real random fluctuations can be seen. For larger bacterial populations, the deterministic response models the growth very well. The stochastic model can also model large groups but requires large number of realisations which causes simulations to take a lot longer to run. |
<br><br> | <br><br> | ||
| - | When | + | When we originally ran the models, we picked arbitrary constants to view the general response. Later we created a code which was able to produce a line of best fit for fluorescence data from the lab; from this line the constants (a1,b1,d1,k1) could be determined. |
<br><br> | <br><br> | ||
Revision as of 23:56, 17 October 2014


























 "
"








 Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.
Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.



 Oxford iGEM 2014
Oxford iGEM 2014














 This simplifies the equation to:
This simplifies the equation to:
 As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
 Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:
Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:

 alongside the correct inputs:
alongside the correct inputs:
 The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
 Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:
Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:


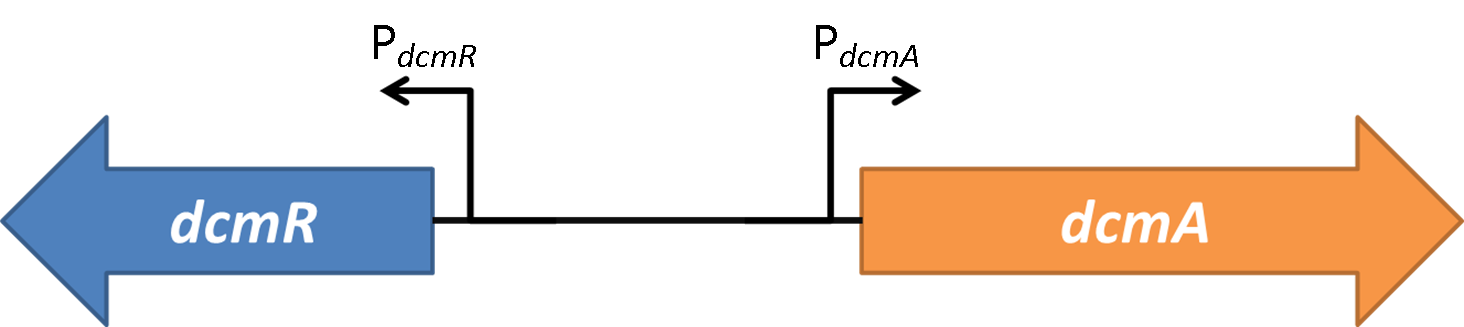
 The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
 The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
 Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!
Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!



































