Team:Oxford/biosensor characterisation
From 2014.igem.org
(Difference between revisions)
| Line 212: | Line 212: | ||
Where α_0 represents the probability that any reaction will happen, given by the following equation: | Where α_0 represents the probability that any reaction will happen, given by the following equation: | ||
<br> | <br> | ||
| - | <img src="https:// | + | <img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:4%; width:47%;" /> |
<br><br><br> | <br><br><br> | ||
| Line 222: | Line 222: | ||
We only stored the time and amount of GFP when there was a reaction, to save on computation. However this made calculating the mean of realisation harder, but we got over the problem by…. | We only stored the time and amount of GFP when there was a reaction, to save on computation. However this made calculating the mean of realisation harder, but we got over the problem by…. | ||
<br><br> | <br><br> | ||
| - | <img src="https:// | + | <img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:8%; width:47%;" /> |
<br><br> | <br><br> | ||
Stochastic modelling is useful because it can show us the stochastic effects which are often seen in real bacteria. By calculating the variation of the mean of multiple GFP producing bacteria, we can also work out the standard deviation. Then if we assume that the system varies with respect to the normal distribution, we can produce error bounds for the production of GFP. Such that we can say, 90% of the time we can expect the production of GFP from a single bacterium to be within these 2 curves. This could be useful for seeing if results are unexpected, or, if there are multiple outliers, that our model is incorrect. If we average more and more bacteria then the mean curve tend towards the deterministic response. This is to be expected as we are now looking at the system as a whole and fluctuations in the production from individual bacteria are averaged out. In terms of their use, when looking at small amounts of bacterium the stochastic model would be better, because real random fluctuations can be seen. For larger bacterium groups, the deterministic response models the growth very well. The stochastic model can also model large groups but requires large number of realisations which causes simulations to take a lot longer to run. | Stochastic modelling is useful because it can show us the stochastic effects which are often seen in real bacteria. By calculating the variation of the mean of multiple GFP producing bacteria, we can also work out the standard deviation. Then if we assume that the system varies with respect to the normal distribution, we can produce error bounds for the production of GFP. Such that we can say, 90% of the time we can expect the production of GFP from a single bacterium to be within these 2 curves. This could be useful for seeing if results are unexpected, or, if there are multiple outliers, that our model is incorrect. If we average more and more bacteria then the mean curve tend towards the deterministic response. This is to be expected as we are now looking at the system as a whole and fluctuations in the production from individual bacteria are averaged out. In terms of their use, when looking at small amounts of bacterium the stochastic model would be better, because real random fluctuations can be seen. For larger bacterium groups, the deterministic response models the growth very well. The stochastic model can also model large groups but requires large number of realisations which causes simulations to take a lot longer to run. | ||
Revision as of 18:16, 17 October 2014
 "
"








 Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.
Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.



 Oxford iGEM 2014
Oxford iGEM 2014












 This simplifies the equation to:
This simplifies the equation to:
 As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
 Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:
Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:

 alongside the correct inputs:
alongside the correct inputs:
 The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
 Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:
Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:


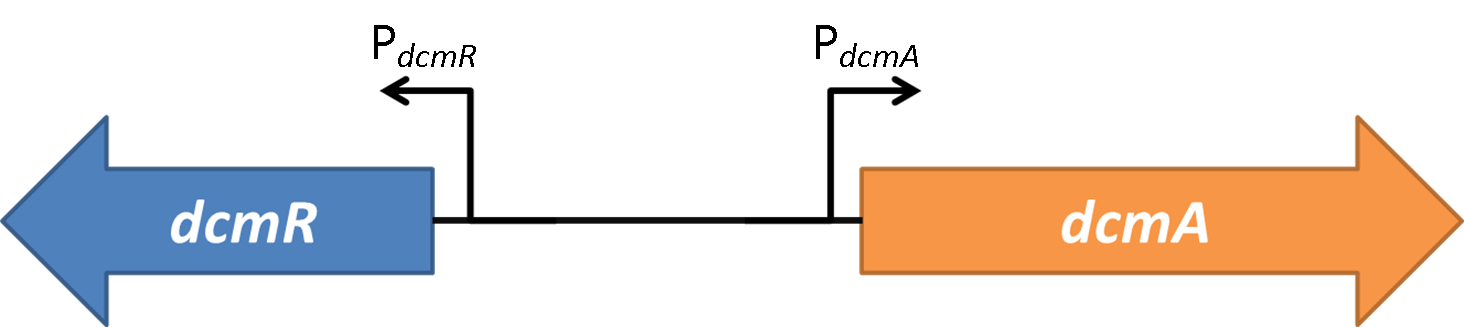
 The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
 The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
 Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!
Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!