Team:Valencia UPV/Modeling/fba
From 2014.igem.org
| Line 120: | Line 120: | ||
<br/> | <br/> | ||
</html> | </html> | ||
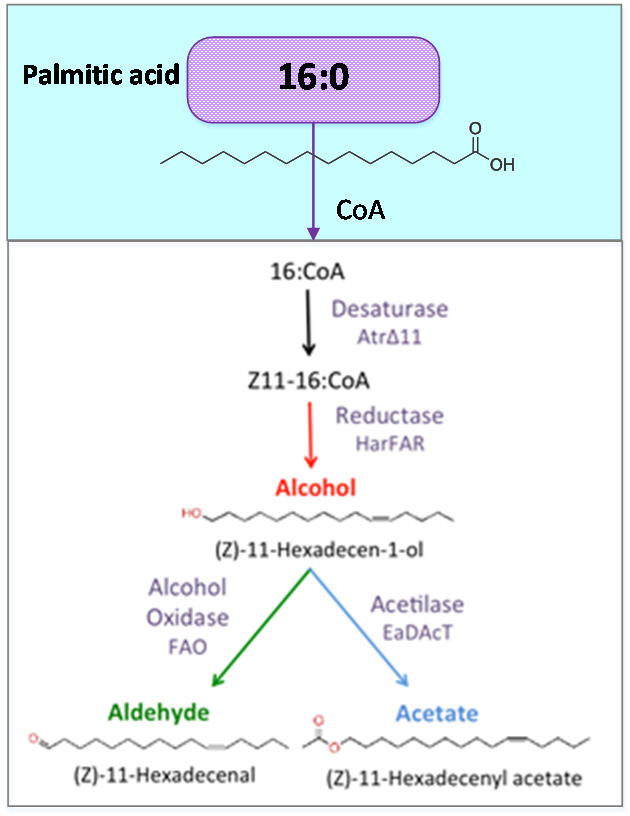
| - | [[File:Precursor.png| | + | [[File:Precursor.png|350px|left|Figure 1. Palmitic acid is a common fatty acid in plants and animals. This metabolite is the precursor of our pheromone. ]] |
<html> | <html> | ||
<p style="text-align: justify; font-style: italic; font-size: 0.8em; width: 700px;"><span class="black-bold">Figure 1</span>. Palmitic acid is a common fatty acid in plants and animals. This metabolite is the precursor of our pheromone.</p> | <p style="text-align: justify; font-style: italic; font-size: 0.8em; width: 700px;"><span class="black-bold">Figure 1</span>. Palmitic acid is a common fatty acid in plants and animals. This metabolite is the precursor of our pheromone.</p> | ||
Revision as of 10:50, 17 October 2014
Modeling > Pheromone Production
The Idea
Pheromones production rates can be estimated using constrained-based modeling of metabolic networks.This can be useful to know the amount of pheromone that can be produced by the synthetic plant.
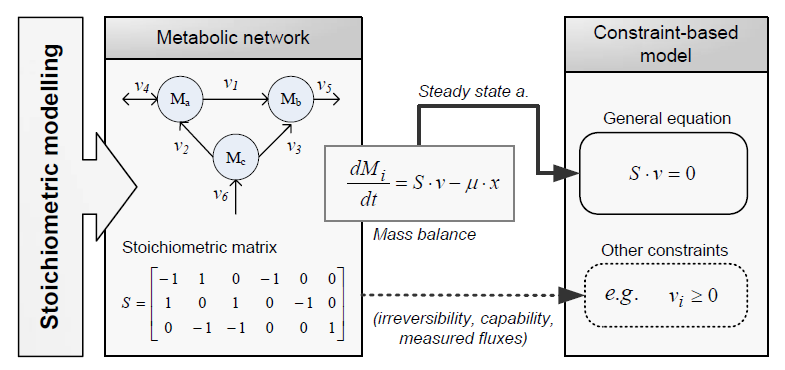
Constraint-based modeling
Constraint-based modeling use models of the cell metabolism that are derived from a metabolic network (stoichiometric models) and assume steady-state for the intracellular metabolites. These two constraints are the base of constraint-based modeling: the fact that cells are subject to constraints that limit their behaviour [1]. In principle, if all constraints operating under a given set of circumstances were known, the actual state of a metabolic network could be elucidated. So by imposing the known constraints, it is possible to determine which functional states can and cannot be achieved by a cell.
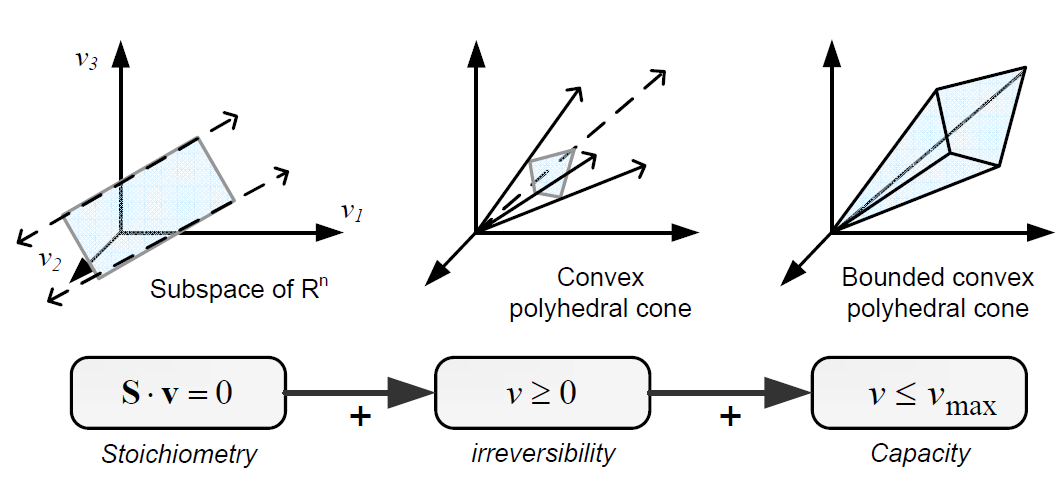
Types of contraints
Constraints can be divided in two main types: non adjustable (invariant) and adjustable ones. The former are time-invariant restrictions of possible cell behaviour, whereas the latter depend on environmental conditions, may change through evolution, and may vary from one individual cell to another. Examples of non adjustable constraints are those imposed by thermodynamics (e.g, irreversibility of fluxes) and enzyme or transport capacities (e.g, maximum flux values). Enzyme kinetics, regulation, and experimental measurements are examples of adjustable constraints. To study the invariant properties of a network, only invariant constraints can be used, because they are those that are always satisfied (i.e, they limit the cell capabilities). If adjustable constraints are used, the elucidated cell states will be only valid under the particular set of circumstances in which these constraints operate [2].
Flux Balance Analysis
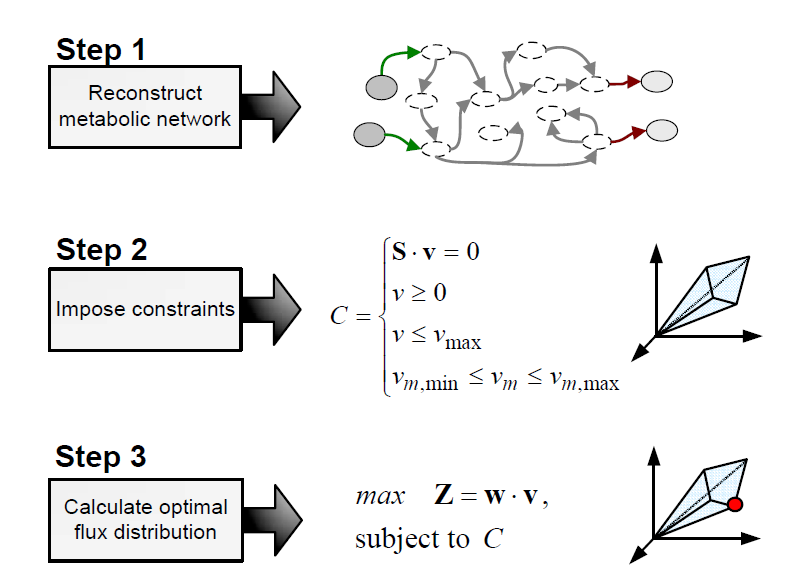
Flux balance analysis (FBA) is a methodology that uses optimisation to get predictions from a constraint-based model by invoking an assumption of optimal cell behaviour. Basically, one particular state among those that cells can show, accordingly to a constraint-based model, is chosen based on the assumption that cells have evolved to be optimal, i.e., that cells regulate its fluxes toward optimal flux states. The following procedure is used to develop a flux balance analysis model:
Flux balance analysis is used to investigate hypothesis (e.g., test if a reduced uptake capacity can be the cause of an unexpected cell behaviour) and to evaluate a range of possibilities (e.g, find the best combination of substrates).
Metabolic objectives and optimization
It must be taken into account that FBA predictions, the optimal flux state, may not correspond to the actual fluxes exhibited by cells. To support the assumption of optimal behaviour, it must be hypothesised that: (i) cells, forced by evolutionary pressure, evolved to achieve an optimal behaviour with respect to certain objective, (ii) we know which this objective is, and (iii) the objective can be expressed, at least approximately, in convenient mathematical terms.
Clearly, predictions of flux balance analysis are dependent on the objective function being used. To date, the most commonly used objective function has been the maximisation of biomass, which leaded to predictions consistent with experimental data for different organisms, such as Escherichia coli [3].
Genome-scale and plant models
FBA is widely used for predicting metabolism, in particular the genome-scale metabolic network reconstructions that have been built in the past decade. These reconstructions contain all of the known metabolic reactions in an organism, and the genes that encode each enzyme. In our case, FBA will calculate the flow of metabolites through our metabolic network to obtain the maximum production of pheromone. It must be noted that plant genome-scale models are very rare and, indeed, plant FBA is a very new research topic. One of the very few available plant models is the AraGEM model [4], a genome-scale of Arabidopsis Thaliana.
References
- Palsson BO (2006). Systems biology: properties of reconstructed networks. New York, USA: Cambridge University Press New York.
- Llaneras F, Picó J (2008). Stoichiometric Modelling of Cell Metabolism. Journal of Bioscience and Bioengineering, 105:1.
- Edwards JS, Covert M, Palsson B (2002). Metabolic modelling of microbes: the flux-balance approach. Environmental Microbiology, 4:133-140.
- de Oliveira Dal'Molin CG1, Quek LE, Palfreyman RW, Brumbley SM, Nielsen LK. AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. NCBI, Plant Physiol. 2010 Feb;152(2):579-89. doi: 10.1104/pp.109.148817. Epub 2009 Dec 31.
COBRA
The COnstraints Based Reconstruction and Analysis (COBRA) approach to systems biology accepts the fact that we do not possess sufficiently detailed parameter data to precisely model, in the biophysical sense, an organism or plant at the genome scale [1]. The COBRA Toolbox is a freely available Matlab toolbox can be used to perform a variety of COBRA methods, including many FBA-based methods. Models for the COBRA Toolbox are saved in the Systems Biology Markup Language (SBML).
AraGEM Model
AraGEM [2] is the genome-scale metabolic network model covering primary metabolism for a compartmentalized plant cell based on the Arabidopsis (Arabidopsis Thaliana) genome. AraGEM is a comprehensive literature-based model, that accounts for the functions of 1,419 unique open reading frames, 1,748 metabolites, 5,253 gene-enzyme reaction-association entries, and 1,567 unique reactions compartmentalized into the cytoplasm, mitochondrion, plastid, peroxisome, and vacuole. Using efficient resource utilization as the optimality criterion, AraGEM has already been used to predict the classical photorespiratory cycle as well as known key differences between redox metabolism in photosynthetic and nonphotosynthetic plant cells.
AraGEM is a viable framework for in silico functional analysis and can be used to derive new, nontrivial hypotheses for exploring plant metabolism. We take for granted that AraGEM is the genome-scale metabolic network model that currently better approximates the metabolism model of N. benthamiana. In Sexy Plant we have added in silico the reactions from the network of pheromone production. As optimality criterion we sought to maximize the pheromone flux produced by the plant.
Pheromone pathway location
Figure 1. Palmitic acid is a common fatty acid in plants and animals. This metabolite is the precursor of our pheromone.
Palmitic acid (16:0) is the most common fatty acid (saturated) found in animals, plants and microorganisms.
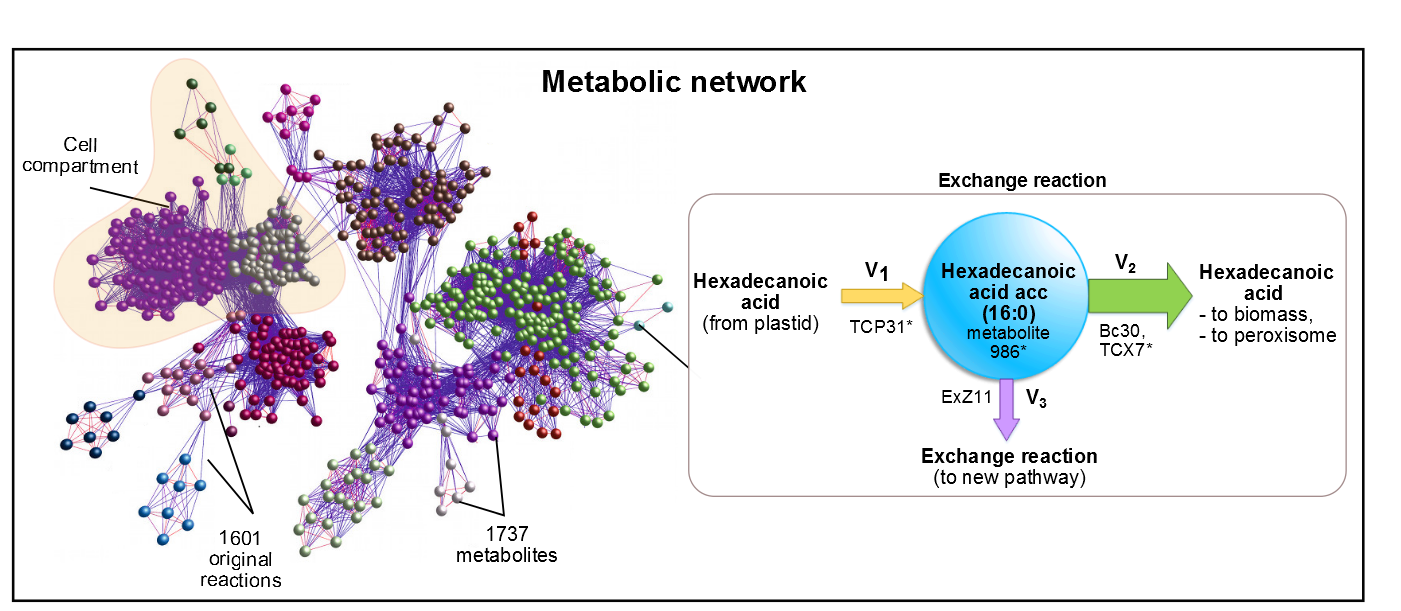
As precursor of our pathway, our efforts were aimed at the optimization of palmitic acid. In the AraGEM model, this is denoted as Hexadecanoic acid_acc (16:0) and is located in the cytosol (see Figure 1). To model the pathway, we introduced the reaction using one influx V1 and two effluxes V2, V3 (see Figure 2). The efflux V2 was incorporated as an exchange reaction, in order to generate a branch in the original pathway of 16:0 metabolism. As our metabolic pathway is linear, starting from 16:0, this new added branch represents the whole synthetic pathway of our pheromone.
Figure 2. In AraGEM, palmitic acid is also called Hexadecanoic32 Acid_acc. The reaction added ExZ11 produces the efflux V3 known as palmitic acidexchange.
Defining scenarios
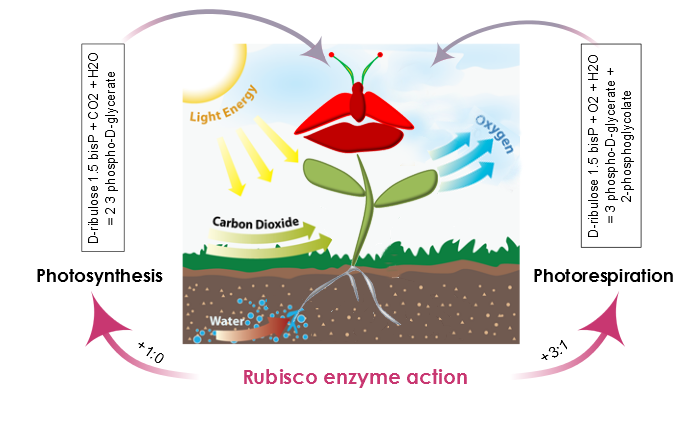
AraGEM is a generic plant cell model capable of representing both photosynthetic and nonphotosynthetic cell types [1]. In order to reproduce the classical physiological scenarios of plant cell metabolism, we explored two photosynthetic scenarios: i) Photosynthesis and ii) Photorespiration. The difference comes from the carboxylation reaction of Rubisco. This enzyme in the presence of oxygen (O2) reduces the energy efficiency of photosynthetic output by 25% in C3 plants.
Figure 3. Rubisco enzyme action defines two scenarios in plant metabolism: Photosynthesis and Photorespiration. During Photosynthesis, the carboxylation-oxygenation ratio is +1:0 and there is no oxygenation of ribulose 1.5-bisP. Moreover, the presence of oxygen and rubisco also catalyzes an oxygen reaction, photosynthesis efficiency is reduced and the carboxylation-oxygenation ratio is +3:1.
Model assumptions
In plants, the most genome-scale metabolic network reconstructions minimize the photons consumption (Ex16) while growth rate or biomass (BIO_L) rate is kept fixed. This is true if we mainly seek the survival of the plant, and photons consumption will be the optimization objective.
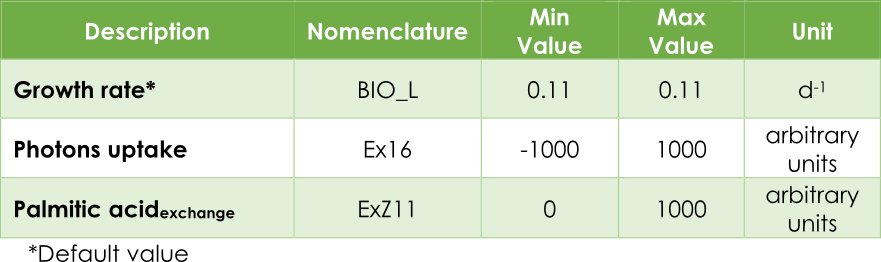
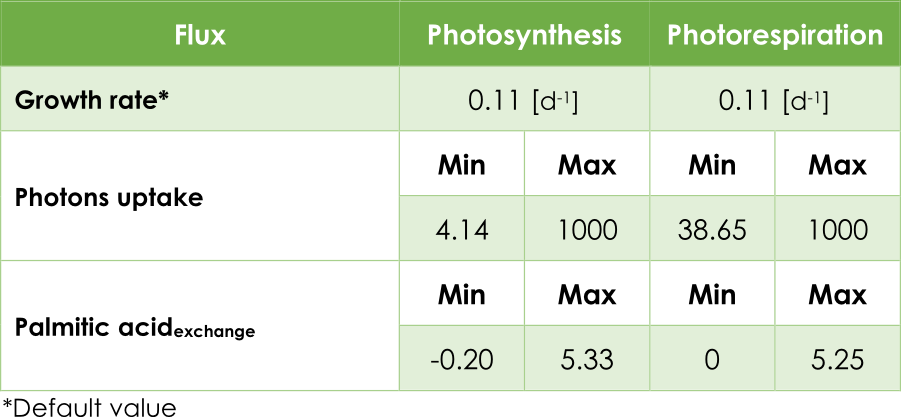
In our case, the principal objective is maximizing the pheromone production, in other words, optimizing the efflux V3 from the exchange reaction ExZ11. In addition, we must introduce the low (lb) and up (ub) bound for each reaction. In AraGEM, the bounds for flux reactions Ex16, BIO_L and ExZ11 were fitted according to Table 1.
Table 1. Upper and lower bounds in AraGEM.
Optimal pheromone production using FBA
Table 2. FBA results in each scenario.
The optimum flux distribution is here defined as the flux distribution that maximizes palmitic acid flux, for a fixed rate of biomass synthesis and free photon uptake.
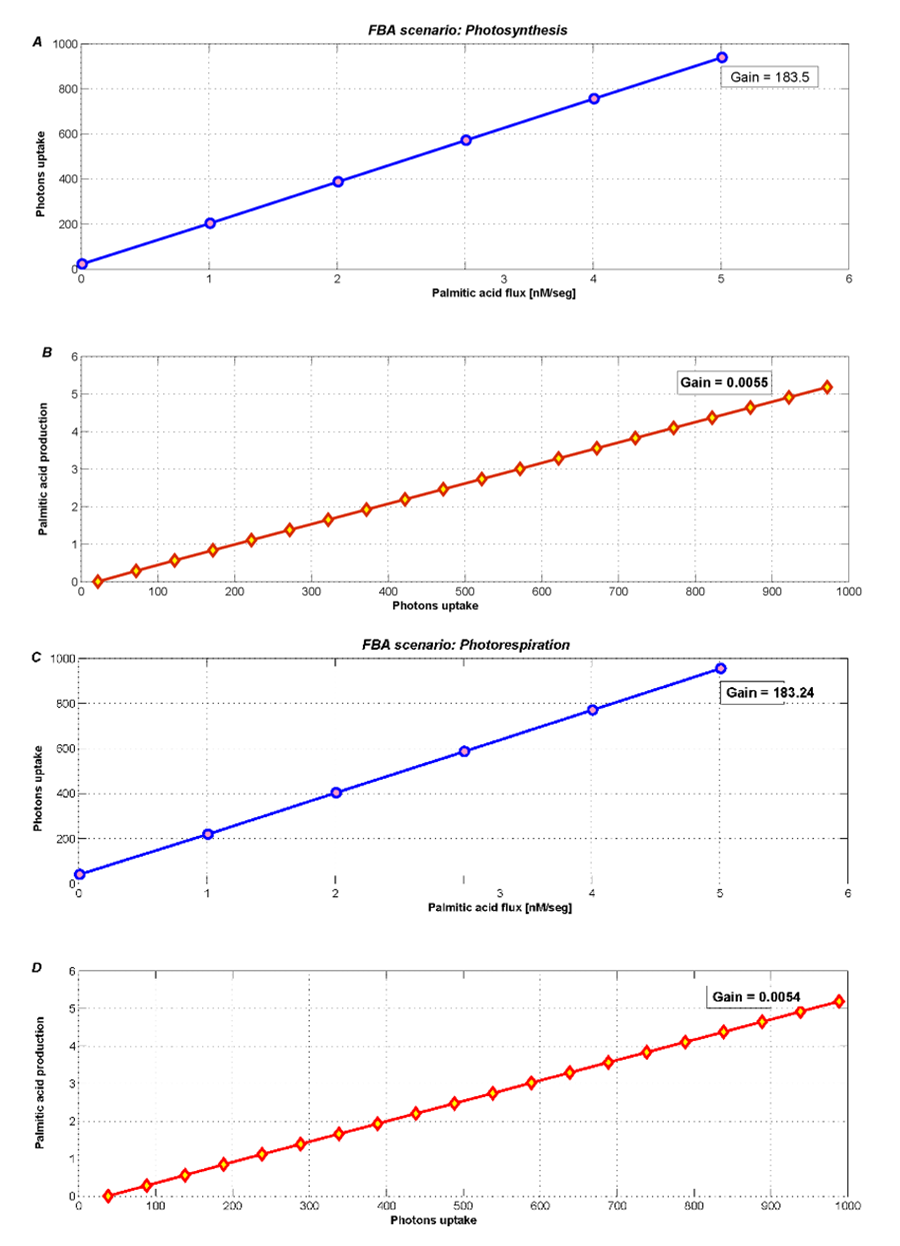
The metabolic contrast between photosynthesis and photorespiration is illustrated in Figure 4. Photosynthesis (Figure 4A and 4B) shows an increase of the palmitic acidexchange flux, when the photons uptake are unconstraint and takes values until 1000 (default maximum flux COBRA).
Even when the photons flux freely increase, the most palmitic acid is used by the biomass or plant growth. Therefore, the new palmitic acid_{exchange} flux only becomes 5.33 nM/seg. However, this level also depends of the high growth rate fixed from the literature.
Figure 4. Optimization during photosynthesis with two different objectives fluxes A) minimizing photons uptake and B) maximizing palmitic acidexchange. During photorespiration, metabolism products decrease, such as C) photons uptake and D) palmitic acidexchange.
During photorespiration, we used FBA to optimize and analyze both palmitic acidexchange and photons uptake. Figure 4C and 4D shows an imperceptible loss (2%) in the palmitic acidexchange flux. The new flux is 5.24 nM/seg and its behavior is similar to the photosynthesis scenario.
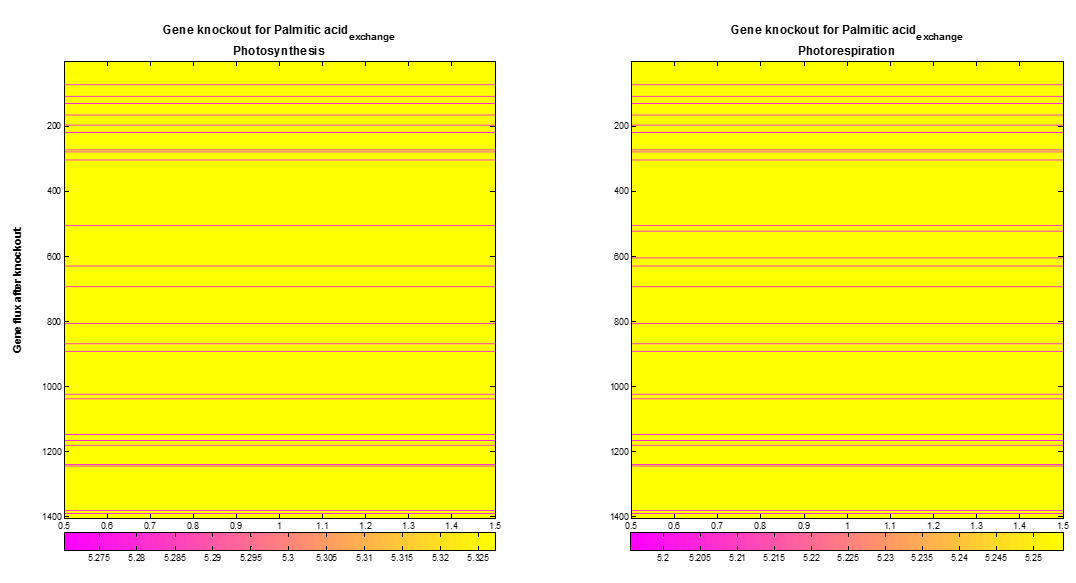
We included a supplementary analysis produced by FBA optimization called Gene knockout. COBRA toolbox knock outs one by one gene of the AraGEM model to optimize the desired objective flux. The Figure 5 shows the maximum palmitic acidexchange flux obtained after gene knockout of each gene During photosynthesis or photorespiration, the optimal palmitic acidexchange flux presents a decrease when around 33 from 1404 gene were knocked out.
Figure 5. Palmitic acidexchange flux after gene knockout. From 1404 gene in AraGEM model, 33 (pink lines) gene show an influence over the optimal Palmitic acidexchange flux.
References
- Daniel Hyduke, Jan Schellenberger, Richard Que, Ronan Fleming, Ines Thiele, Jeffery Orth, Adam Feist, Daniel Zielinski, Aarash Bordbar, Nathan Lewis, Sorena Rahmanian, Joseph Kang & Bernhard Palsson. COBRA Toolbox 2.0 Link: http://systemsbiology.ucsd.edu/Downloads/Cobra_Toolbox.
- de Oliveira Dal'Molin CG1, Quek LE, Palfreyman RW, Brumbley SM, Nielsen LK. AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. NCBI, Plant Physiol. 2010 Feb;152(2):579-89. doi: 10.1104/pp.109.148817. Epub 2009 Dec 31.
- Rajib Saha,Patrick F. Suthers, Costas D. Maranas mail. Zea mays iRS1563: A Comprehensive Genome-Scale Metabolic Reconstruction of Maize Metabolism. Plos One. Published: July 06, 2011 DOI: 10.1371/journal.pone.0021784.
NetLogo is an agent-based programming language and integrated modeling environment. NetLogo is free and open source software, under a GPL license.
Tab #4 content goes here!
Donec pulvinar neque sed semper lacinia. Curabitur lacinia ullamcorper nibh; quis imperdiet velit eleifend ac. Donec blandit mauris eget aliquet lacinia! Donec pulvinar massa interdum risus ornare mollis. In hac habitasse platea dictumst. Ut euismod tempus hendrerit. Morbi ut adipiscing nisi. Etiam rutrum sodales gravida! Aliquam tellus orci, iaculis vel.
Go to Modeling Overview Go to Diffusion and Moth Response
 "
"