Team:ETH Zurich/labblog/20140829mod
From 2014.igem.org
| Line 1: | Line 1: | ||
| - | <html><article class="all modeling parameter" date="20140829"></html> | + | <html><article class="all modeling parameter" id="intparam" date="20140829"></html> |
== Integrase parameters == | == Integrase parameters == | ||
Revision as of 10:51, 8 September 2014
Integrase parameters
Friday, August 29th
In order to predict accurately the experiments we designed, we defined two different strategies to retrieve parameters for the integrase system.
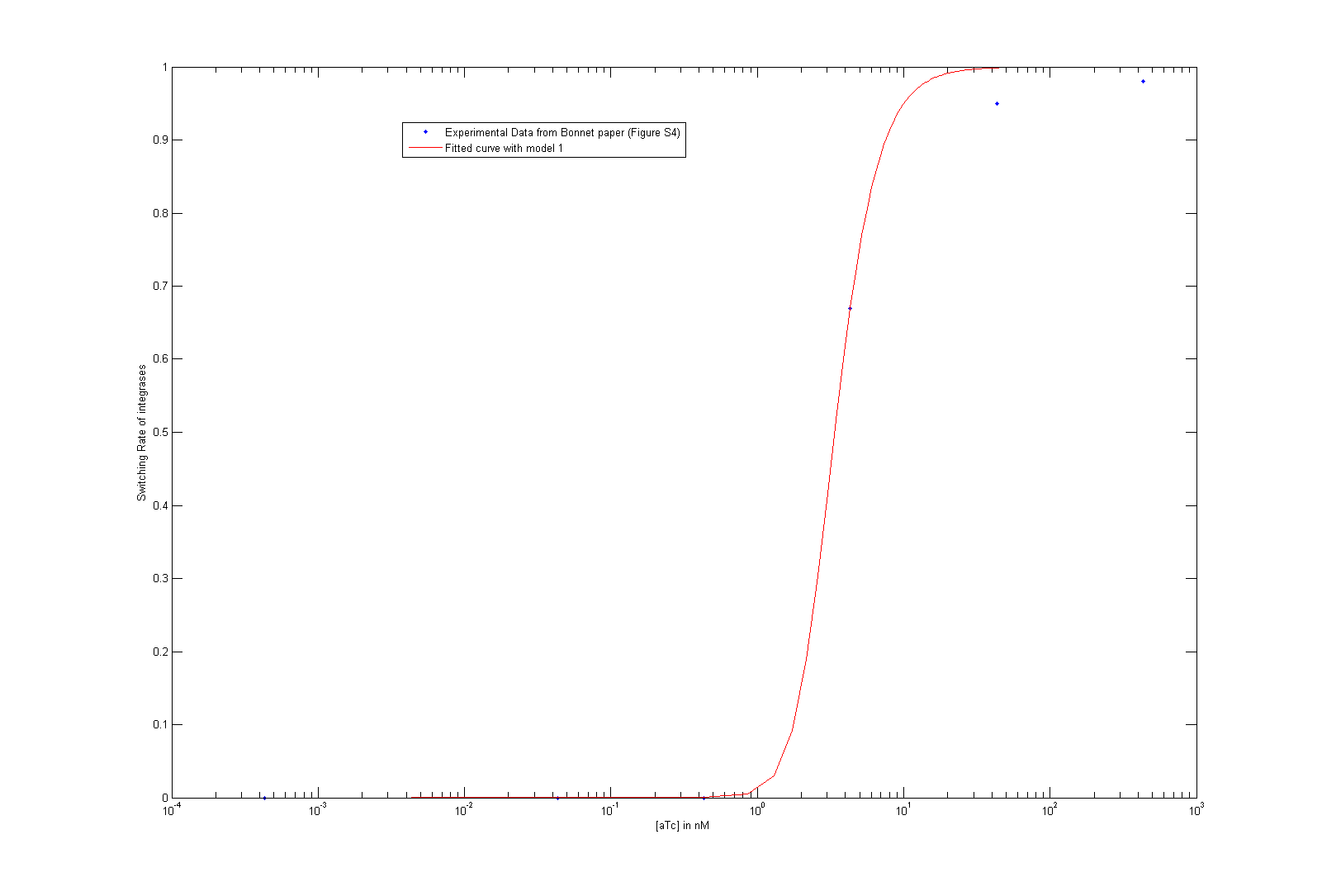
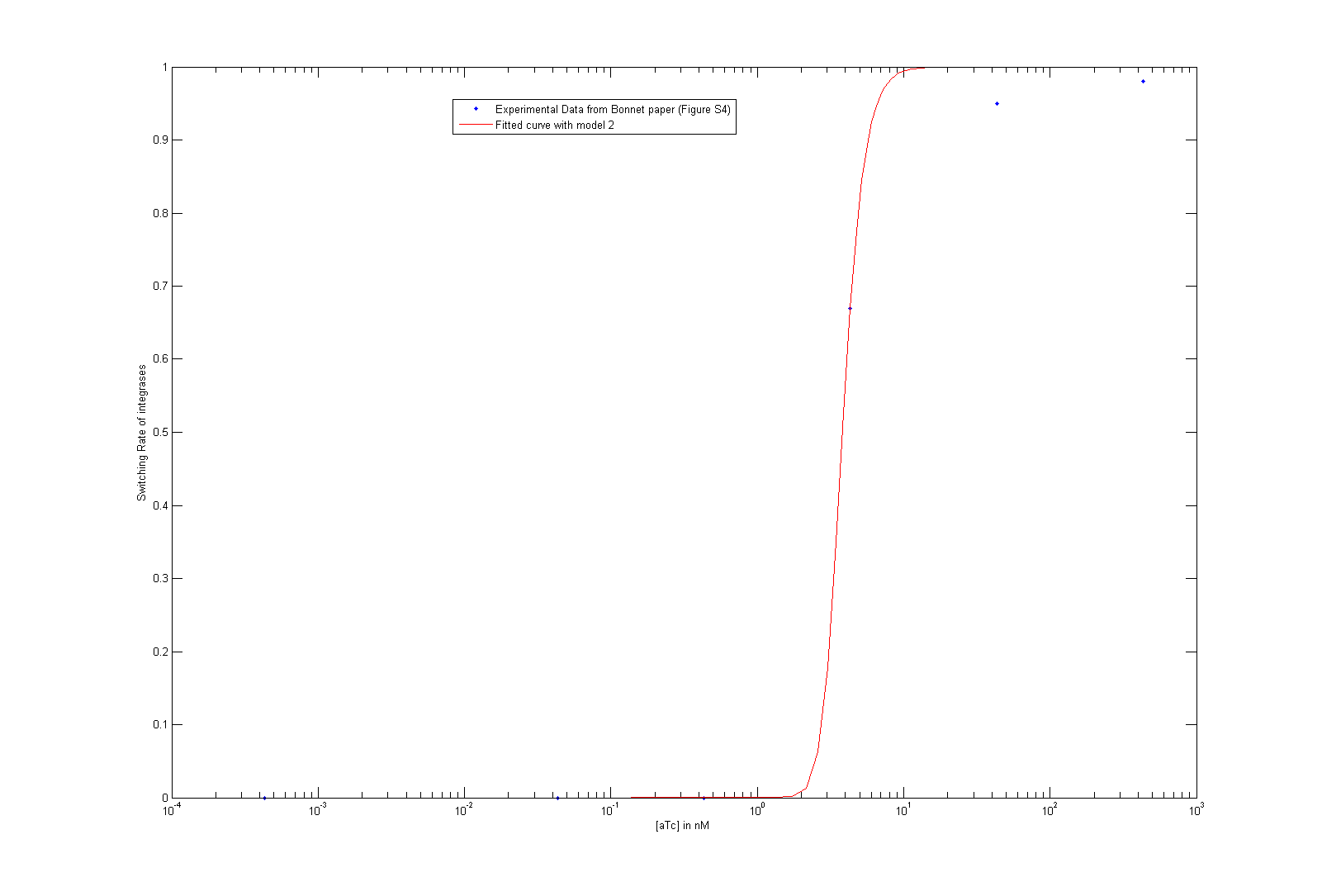
As we did not find these parameters on the web, we used the data given by the Bonnet paper "Amplifying genetic logic gates". The figure S4 is particularly interesting, even if it does not give any information on the dynamics of the system. We modeled and wrote the equations corresponding to Bonnet's experiment.
At first, we try to fit the dynamic parameters of the system with only the steady states values. To fit the parameters with the data, we first try to use a minimum search for the difference between the data and the parametric function. Then, using these first approximations, we tried to do a Markov Chain Monte Carlo approach to find a more suited curve. As these two methods are strongly prior dependent, we planned another step of screening in order to have meaningful results. However, our knowledge on the parameters, the number of data points compared to the high number of parameters did not give any meaningful results.
We then decided to simplify our system :
- We consider that Bxb1a and Bxb1b have the same behavior. Therefore, they don't appear as differentiated in our system anymore.
- The paper uses the tet system to induce their system. This was modeled explicitly before. We approximated this part to a Hill function, which takes leakiness into consideration. The parameters for the Hill function are the result from a study of an other iGEM team UCSF from last year. Please visit their page for more information. The same biobrick is indeed used in their work and in Bonnet's paper.
- We consider that the dimer of the integrase and the binding to DNA were at quasi steady-state.
As we tried to fit the steady state, we obtained two different models, depending on which assumption we made. As these two models fit the Bonnet's curve well, we used them both to derive more precisely the dissociation constant of the dimerization reaction and the one of the DNA binding reaction. Each of them appear in one of the lumped parameters we fitted.
By considering reasonable order of magnitude for other parameters present in the lumped parameters, we find that the value of the dissociation constants are both of the order of 10-4. This order of magnitude is not surprising at all, as we know that the binding of integrases to DNA is very specific (which is underlined by the low value of the dissociation constant of this reaction) and that integrases are more stable as dimer than as monomer.
 "
"