Team:Oxford/biosensor characterisation
From 2014.igem.org
(Difference between revisions)
MatthewBooth (Talk | contribs) |
|||
| Line 205: | Line 205: | ||
<br><br> | <br><br> | ||
| - | We started with the Gillespie Algorithm, which considers the expression of GFP to be binary; a molecule of GFP is either produced or degraded. Before we determined which reaction happened, we had to work out when the reaction happened. Using the random number r ( | + | We started with the Gillespie Algorithm, which considers the expression of GFP to be binary; a molecule of GFP is either produced or degraded. Before we determined which reaction happened, we had to work out when the reaction happened. Using the random number r (taken from a uniform distribution between 0 and 1), we produced another random number τ, which determined the time until the next reaction. |
<br><br> | <br><br> | ||
equation here | equation here | ||
<br><br> | <br><br> | ||
| - | Where | + | Where α_0 represents the probability that any reaction will happen, given by the following equation: |
<br><br> | <br><br> | ||
equation here | equation here | ||
<br><br> | <br><br> | ||
| - | We modelled the probability of a molecule of GFP being created using the Michaelis-Menten model ( | + | We modelled the probability of a molecule of GFP being created using the Michaelis-Menten model (α_1), incorporating a basal transcription rate (beta1). For the degradation, we assumed a simple proportional relationship; the more GFP you have the more likely it is that a molecule degrades (δ_1). The constant of proportionality will be a function of the intrinsic life time of the protein in the cell. We considered there to be no DCM originally, then a large step in DCM at time=0. This is similar to placing the detector in a DCM polluted source, to make the model more realistic the level of DCM would go down as it is degraded but we had no time to obtain data for this rate. |
<br><br> | <br><br> | ||
| - | To decide if GFP was produced, we looked at the percentage of “reactions” which were productions, and then we compared this to a second random number (uniform distribution from 0 to 1). If the random number was lower, then GFP was created. If it was higher, then a GFP was degraded. In this way we make a weighted random choice about whether GFP was created or degraded | + | To decide if GFP was produced, we looked at the percentage of “reactions” which were productions, and then we compared this to a second random number (again taken from a uniform distribution from 0 to 1). If the random number was lower, then a GFP was created. If it was higher, then a GFP was degraded. In this way we make a weighted random choice about whether GFP was created or degraded. |
| + | <br><br> | ||
| + | We only stored the time and amount of GFP when there was a reaction, to save on computation. However this made calculating the mean of realisation harder, but we got over the problem by…. | ||
<br><br> | <br><br> | ||
equation here | equation here | ||
Revision as of 17:45, 17 October 2014
 "
"








 Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.
Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.



 Oxford iGEM 2014
Oxford iGEM 2014











 This simplifies the equation to:
This simplifies the equation to:
 As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
 Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:
Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:

 alongside the correct inputs:
alongside the correct inputs:
 The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
 Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:
Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:


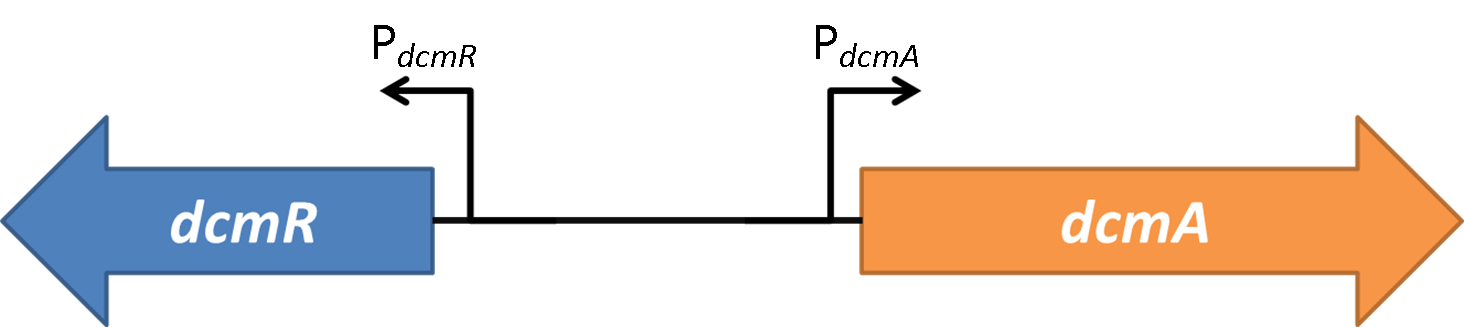
 The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
The first system that we tested is shown here. This is the bottom level of our synthetic circuit. Testing just this plasmid allowed us to obtain some important information to allow us to characterise the genetic system.
 The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
The second system that we tested was the whole synthetic system without any DCM added. This allowed us to analyse just the effect of DcmR on the PdcmA promoter when it was compared to the result from system 1.
 Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!
Therefore we know that DcmR represses PdcmA with DCM repressing this repression. This means that the system is a double repressor!