Team:ETH Zurich/modeling/diffmodel
From 2014.igem.org
(→Equations) |
(→Deriving diffusion rates) |
||
| Line 69: | Line 69: | ||
| - | According to Fick's law of diffusion, the | + | According to Fick's law of diffusion, the flows of AHL (number of molecules per second) diffusing from the bead into all cells and from all cells into the bead is |
| - | $$\Phi(AHL_{bead \rightarrow | + | $$\Phi(AHL_{bead \rightarrow cells}) = \sigma \mathcal{A} ([AHL_{ext}]-[AHL_{int}]) \\ \Phi(AHL_{cells \rightarrow bead }) = N \sigma \mathcal{A} ([AHL_{int}]-[AHL_{ext}])$$ |
where σ is the membrane permeability and A is the area of the membrane. | where σ is the membrane permeability and A is the area of the membrane. | ||
Revision as of 16:57, 15 October 2014
Diffusion model
Model
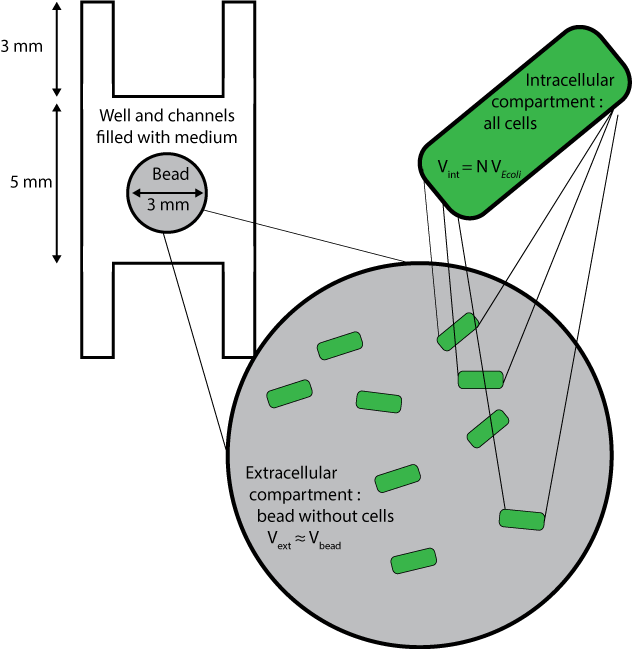
The main experiment for investigating diffusion is a propagation of the whole pattern through the chip via the quorum sensing module only. We have used beads containing cells which are able to sense luxAHL, produce GFP when they sense it, and amplify the signal for the next row. The combination of the quorum sensing module with diffusion enables to check that cells will amplify the signal enough from one row to the next one, and to check what would be the time scale of the pattern formation.
We used a reaction-diffusion model to combine quorum sensing reactions and diffusion. Here are the different compartments considered :
Species
| Name | Description |
|---|---|
| LuxAHLint | LuxAHL inside cells |
| LuxAHLext | LuxAHL outside cells |
| LuxR | Constitutively expressed regulator protein that can bind LuxAHL and stimulate transcription of GFP. |
| RLux | LuxR and LuxAHL complex which can dimerize. |
| mRNAGFP | mRNA for Green fluorescent protein which is produced when the cells are ON. |
| GFP | Green fluorescent protein which is produced when the cells are ON. |
| mRNALuxI | mRNA for LuxI which is produced when the cells are ON. |
| LuxI | Enzyme catalysing the production of LuxAHL from SAM and ACP. |
The beads are the compartments containing the cells. The number of cells per bead is called N. The fraction of volume occupied by cells to total bead volume is $$\frac{V_{\text{internal to cells}}}{V_{\text{bead}}}=N \ \ V_{E. coli}$$
Reactions
$$ \begin{align} \emptyset&\rightarrow LuxR \\ LuxAHLext & \leftrightarrow LuxAHLint\\ LuxAHLint+LuxR & \leftrightarrow RLux\\ RLux+RLux &\leftrightarrow DRLux\\ DRLux+P_{luxOFF} & \leftrightarrow P_{luxON}\\ P_{luxON}&\rightarrow P_{luxON}+mRNA_{GFP}\\ mRNA_{GFP}&\rightarrow GFP \end{align}$$
Equations
Deriving diffusion rates
We are using a reaction-diffusion model, which means that for internal and external AHL species which diffuse, we have to include a diffusion rate in addition to reaction rates :
$$\frac{d[AHL]}{dt}=\mathcal{Diff}(AHL)+\mathcal{R}(AHL)$$
According to Fick's law of diffusion, the flows of AHL (number of molecules per second) diffusing from the bead into all cells and from all cells into the bead is
$$\Phi(AHL_{bead \rightarrow cells}) = \sigma \mathcal{A} ([AHL_{ext}]-[AHL_{int}]) \\ \Phi(AHL_{cells \rightarrow bead }) = N \sigma \mathcal{A} ([AHL_{int}]-[AHL_{ext}])$$
where σ is the membrane permeability and A is the area of the membrane.
The flow of internal AHL diffusing from the cells into the bead compartment is $$N \sigma \mathcal{A} ([AHL_{int}]-[AHL_{ext}]) $$ where N is the total number of cells.
Thus the diffusion rate of internal AHL (concentration per second) is : $$Diff(AHL_{int})=\frac{\sigma \mathcal{A}}{V_{E. coli}} ([AHL_{ext}]-[AHL_{int}])=D_m ([AHL_{ext}-[AHL_{int}])$$ where Dm is a lumped coefficient for diffusion through the membrane,
and the diffusion rate of external AHL is $$Diff(AHL_{ext})=\frac{N \sigma \mathcal{A}}{V_{bead}} ([AHL_{ext}]-[AHL_{int}])= \frac{N V_{E.coli}}{V_{bead}}D_m([AHL_{ext}]-[AHL_{int}])=\rho V_{E.coli}D_m([AHL_{ext}]-[AHL_{int}])$$ where ρ is the cell density (number of cells per bead).
Set of equations
$$ \begin{align*} \frac{d[AHLext]}{dt} &= \rho \ V_{E. coli}\ D_m (LuxAHL_{int}-AHL_{ext}) -d_{AHLext}[AHL_{ext}]\\ \frac{d[AHLint]}{dt} &= Dm (LuxAHL_{ext}-AHL_{int}) + k_{-RLux}[R_{Lux}]-k_{RLux}[LuxAHL_{int}][LuxR]-d_{AHLint}[AHL_{int}]\\ \frac{d[LuxR]}{dt} &= \alpha_{LuxR} -k_{RLux}[AHL_{int}][LuxR] + k_{-RLux}[RLux] - d_{LuxR}[LuxR] \\ \frac{d[RLux]}{dt} &= k_{RLux}[AHL_{int}][LuxR] - k_{-RLux}[RLux] - d_{RLux} [RLux] \\ \frac{d[mRNA_{GFP}]}{dt} &= \frac{k_{mRNA_{GFP}}[RLux]^2}{K_{mLux}^2 + [RLux]^2}- d_{mRNA_{GFP}} [mRNA_{GFP}]\\ \frac{d[GFP]}{dt} &= k_{GFP} [mRNA_{GFP}] - d_{GFP}[GFP]\\ \end{align*} $$
Results
 "
"