Team:Oxford/biosensor characterisation
From 2014.igem.org
(Difference between revisions)
| (31 intermediate revisions not shown) | |||
| Line 54: | Line 54: | ||
<br><br> | <br><br> | ||
| - | + | ||
| Line 139: | Line 139: | ||
<h1>Predicting the mCherry fluorescence</h1> | <h1>Predicting the mCherry fluorescence</h1> | ||
| - | We simplified the first double repression by modelling it as an activation of <font style="font-style: italic;">dcmR</font> by | + | We simplified the first double repression by modelling it as an activation of <font style="font-style: italic;">dcmR</font> by anhydrous-tetracycline (ATC), albeit parameterised by different constants. This assumption is justified by the fact that we are able to precisely control the addition of ATC and measure the fluorescence of the mCherry. |
<br> | <br> | ||
<br> | <br> | ||
| Line 201: | Line 201: | ||
</div> | </div> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| Line 287: | Line 256: | ||
<h1>Predicting the sfGFP fluorescence</h1> | <h1>Predicting the sfGFP fluorescence</h1> | ||
<h1>Introduction</h1> | <h1>Introduction</h1> | ||
| - | To allow us to characterize the second half of the genetic circuit, we needed to be able to predict the difference in response. To do this, we constructed models by cascading the differential equations according to the respective circuit structures thereby producing two different potential system responses. | + | To allow us to characterize the second half of the genetic circuit (DcmR regulating sfGFP), we needed to be able to predict the difference in response. To do this, we constructed models by cascading the differential equations according to the respective circuit structures thereby producing two different potential system responses. |
<br><br> | <br><br> | ||
We then set up the differential equations necessary to solve this problem in Matlab. The method and results are as detailed below: | We then set up the differential equations necessary to solve this problem in Matlab. The method and results are as detailed below: | ||
| Line 390: | Line 359: | ||
<br><br> | <br><br> | ||
| - | We started with the Gillespie Algorithm, which considers the expression of mCherry to be binary; a molecule of | + | We started with the Gillespie Algorithm, which considers the expression of mCherry to be binary; a molecule of mCherry is either expressed or degraded. Before we determined which event happened, we had to work out when the event happened. Using the random number r1 (taken from a uniform distribution between 0 and 1), we produced another random number τ, which determined the time until the next reaction. |
<br><br> | <br><br> | ||
<img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:8%; width:20%;" /> | <img src="https://static.igem.org/mediawiki/2014/8/89/Oxford_Matt_equations_1.jpg" style="float:left;position:relative; height:8%; width:20%;" /> | ||
| Line 408: | Line 377: | ||
<br><br><br><br><br><br><br><br> | <br><br><br><br><br><br><br><br> | ||
| - | Stochastic modelling is useful because it can show us the stochastic effects which are often observed in individual bacteria. By calculating the variation of the mean of multiple mCherry producing bacteria, we can also work out the standard deviation. Then if we assume that the system varies with respect to the normal distribution, we can produce error bounds for the production of | + | Stochastic modelling is useful because it can show us the stochastic effects which are often observed in individual bacteria. By calculating the variation of the mean of multiple mCherry producing bacteria, we can also work out the standard deviation. Then if we assume that the system varies with respect to the normal distribution, we can produce error bounds for the production of mCherry, such that we can say that 90% of the time we can expect the production of mCherry from a single bacterium to be within these two curves as seen in Figure 2. This could be useful for seeing if results are unexpected, or, if there are multiple outliers, that our model is incorrect. If we average an increasing number of bacteria, then the mean stochastic curve tends towards the deterministic response as seen in Figure 1. This is to be expected, as we are now looking at the system as a whole and fluctuations in the production from individual bacteria are averaged out. In terms of their use, when looking at small amounts of bacterium the stochastic model would be better, because real random fluctuations can be seen. For larger bacterial populations, the deterministic response models the growth very well. The stochastic model can also model large groups but requires large number of realisations which causes simulations to take a lot longer to run. |
<br><br> | <br><br> | ||
| Line 422: | Line 391: | ||
<br><br> | <br><br> | ||
| - | However, because the of the size of expression term | + | However, because the of the size of expression term, the time between events are very small resulting in an almost deterministic response even with only 1 realisation as can be seen on Figure 3. |
<br><br> | <br><br> | ||
α1 = expression rate constant of dcmR = 16.5min-1 | α1 = expression rate constant of dcmR = 16.5min-1 | ||
| Line 489: | Line 458: | ||
<img src="https://static.igem.org/mediawiki/parts/5/51/Oxford_DcmR-mCherry_expression_induced_by_0ng_ATC.png" | <img src="https://static.igem.org/mediawiki/parts/5/51/Oxford_DcmR-mCherry_expression_induced_by_0ng_ATC.png" | ||
style="float:left;position:relative; width:70%;" /> | style="float:left;position:relative; width:70%;" /> | ||
| - | <img src="https://static.igem.org/mediawiki/parts/1/19/Oxford_DcmR-mCherry_expression_induced_by_10ng_ATC.png" style="float: | + | <img src="https://static.igem.org/mediawiki/parts/1/19/Oxford_DcmR-mCherry_expression_induced_by_10ng_ATC.png" style="float:left;position:relative; width:70%;" /> |
<img src="https://static.igem.org/mediawiki/parts/6/63/Oxford_DcmR-mCherry_expression_induced_by_50ng_ATC.png" style="float:left;position:relative; width:70%;" /> | <img src="https://static.igem.org/mediawiki/parts/6/63/Oxford_DcmR-mCherry_expression_induced_by_50ng_ATC.png" style="float:left;position:relative; width:70%;" /> | ||
| - | <img src="https://static.igem.org/mediawiki/parts/c/cb/Oxford_DcmR-mCherry_expression_induced_by_100ng_ATC.png" style="float: | + | <img src="https://static.igem.org/mediawiki/parts/c/cb/Oxford_DcmR-mCherry_expression_induced_by_100ng_ATC.png" style="float:left;position:relative; width:70%;" /> |
<img src="https://static.igem.org/mediawiki/parts/3/37/Oxford_DcmR-mCherry_expression_induced_by_200ng_ATC.png" style="float:centre;position:relative; width:70%;" /> | <img src="https://static.igem.org/mediawiki/parts/3/37/Oxford_DcmR-mCherry_expression_induced_by_200ng_ATC.png" style="float:centre;position:relative; width:70%;" /> | ||
| - | <img src="https://static.igem.org/mediawiki/parts/e/e6/Oxford_Comparison_of_mean_flouresence_intensity_from_DcmR-mCherry_expression_induced_at_varying_amounts_of_ATC.png" style="float: | + | <img src="https://static.igem.org/mediawiki/parts/e/e6/Oxford_Comparison_of_mean_flouresence_intensity_from_DcmR-mCherry_expression_induced_at_varying_amounts_of_ATC.png" style="float:center;position:relative; width:70%;" /><br><br><br><br> |
| + | |||
| + | <img src="https://static.igem.org/mediawiki/2014/e/e9/Microscopy_of_dcmR-mCherry_induction.png" style="float:center;position:relative; width:70%;margin-left:10%;" /> | ||
| + | <br><br>Figure 1. Epi-fluorescence microscopy images (green channel) of cells expressing dcmR-mCherry fusion induced by 0ng ATC, 50ng ATC,and 200ng (left to right) | ||
| Line 534: | Line 506: | ||
<h1>Introduction</h1> | <h1>Introduction</h1> | ||
| - | + | Our team were able to obtain good data for both the mCherry response of the system and the overall sfGFP response. This bubble shows how we adapted our model to make the most of the mCherry fluorescence data. | |
<br><br> | <br><br> | ||
The original data is shown on the right with error bars showing the standard error of the measurements. | The original data is shown on the right with error bars showing the standard error of the measurements. | ||
| Line 742: | Line 714: | ||
<img src="https://static.igem.org/mediawiki/2014/b/b7/Oxford_CharacGlen1.png" style="float:left;position:relative; width:80%;margin-bottom:2%;margin-left:10%;margin-right:10%;" /> | <img src="https://static.igem.org/mediawiki/2014/b/b7/Oxford_CharacGlen1.png" style="float:left;position:relative; width:80%;margin-bottom:2%;margin-left:10%;margin-right:10%;" /> | ||
| + | |||
The results clearly show a decrease in sfGFP fluorescence upon addition and expression of dcmR. Therefore we can confidently conclude that DcmR acts as a repressor in both directions for the PdcmA and PdcmR promoter. | The results clearly show a decrease in sfGFP fluorescence upon addition and expression of dcmR. Therefore we can confidently conclude that DcmR acts as a repressor in both directions for the PdcmA and PdcmR promoter. | ||
| Line 787: | Line 760: | ||
<br><br> | <br><br> | ||
<img src="https://static.igem.org/mediawiki/2014/7/7f/Oxford_charac3.png" style="float:right;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;" /> | <img src="https://static.igem.org/mediawiki/2014/7/7f/Oxford_charac3.png" style="float:right;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;" /> | ||
| + | <br> | ||
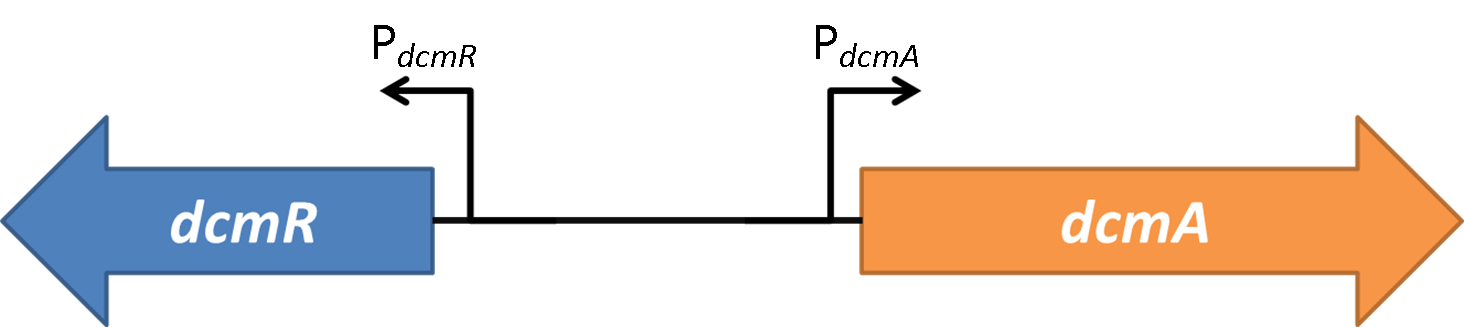
| + | <strong>Figure 2</strong>shows the the gene region under investigation and manipulation in the design of our biosensor. PdcmA and PdcmR describe the two directions of a bidirectional promoter that is bound and modulated by DcmR | ||
| + | <br> | ||
| + | <br> | ||
We can see from these results that at both growth stages the relative expression is weighted towards PdcmR. An interesting result is that in the presence of DcmR this ratio is reduced such that expression through PdcmR is relatively increased while expression through PdcmA is relatively decreased. This result is observed as a decrease in the PdcmA/PdcmR expression ratio. From our results this appears more statistically relevant in stationary phase. The cut off for exponential/stationary phase was set at 600 minutes as seen in the above graph. | We can see from these results that at both growth stages the relative expression is weighted towards PdcmR. An interesting result is that in the presence of DcmR this ratio is reduced such that expression through PdcmR is relatively increased while expression through PdcmA is relatively decreased. This result is observed as a decrease in the PdcmA/PdcmR expression ratio. From our results this appears more statistically relevant in stationary phase. The cut off for exponential/stationary phase was set at 600 minutes as seen in the above graph. | ||
| Line 856: | Line 833: | ||
<br><br> | <br><br> | ||
<img src="https://static.igem.org/mediawiki/2014/c/c0/Oxford_CharacGlen5.png" style="float:right;position:relative; width:60%; margin-right:20%;margin-bottom:2%;margin-left:20%;" /> | <img src="https://static.igem.org/mediawiki/2014/c/c0/Oxford_CharacGlen5.png" style="float:right;position:relative; width:60%; margin-right:20%;margin-bottom:2%;margin-left:20%;" /> | ||
| + | <br><br> | ||
| + | |||
| + | These images taken on an epi-fluorescence microscope (exposure time 0.4seconds) physically show the fluorescence from the same cells as used in the time course study as above. | ||
| + | |||
| + | <img src="https://static.igem.org/mediawiki/2014/1/19/Microscopy_comparison_-_A-E_%2B_and_-DCM.png" style="float:right;position:relative; width:60%; margin-right:20%;margin-bottom:2%;margin-left:20%;" /> | ||
<br><br> | <br><br> | ||
| Line 911: | Line 893: | ||
<div class="list"> | <div class="list"> | ||
<div class="white_news_block2"> | <div class="white_news_block2"> | ||
| + | The data that the sfGFP fluorescence data that the wet-lab team obtained presented the engineering team with the exciting possibility of fully parameterising our model of the synthetic circuit and therefore having the ability to make very good approximations of the overall behaviour of our biosensor. | ||
| + | <br><br> | ||
| + | <h1>Calculating the parameters</h1> | ||
| + | To calculate the parameters for behaviour of the second half of the genetic circuit (DcmR regulating sfGFP), we used a similar approach to the method we used to find the parameters for the top half of the circuit. This involves taking key bits of the data and analysing the corresponding equation. | ||
| + | <br><br> | ||
| + | <h1>Degradation rate constant (δ2)</h1> | ||
| + | The degradation half-life of the GFP protein is well documented in the literature and has a value of approximately 24 hours (1440 mins) [1] . This is very high and is one of the reasons that we chose GFP to be our fluorescence indicator. From this value of the half life, it is possible to calculate the degradation rate constant using mathematics: | ||
| + | <br><br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/5/56/Oxford_CharacOV1.png" style="float:left;position:relative; width:15%; margin-right:85%;margin-bottom:2%;margin-left:0%;" /> | ||
| + | <h1>Basal transcription rate constant (β3)</h1> | ||
| + | To find the basal transcription rate constant of the second half of the system (DcmR regulating sfGFP), we analysed the data of the fluorescence of just the Pdcma and the sfGFP gene. | ||
| + | <br><br> | ||
| + | The data shown on the graphs below shows clearly that the fluorescence stops increasing when the bacteria stop growing in the log phase. This means that we can’t reliably use the data from the stationary phase to provide parameters. We have taken this point to be 500 minutes into the data measurement. | ||
| + | <br><br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/5/59/Oxford_CharacOV2.png" style="float:left;position:relative; width:80%; margin-right:10%;margin-bottom:2%;margin-left:10%;" /> | ||
| + | In terms of the modelling equations, this system is equivalent to setting [DcmR] to zero and ensuring that for this scenario, we set β1 = 0 (basal transcription rate of DcmR) . The mathematics below shows how we used the normalised data to find the basal transcription rate of sfGFP. Note how we’re using equation with parameters α3, β3 and k3 because the wet-lab team were able to prove that DcmR acts as a repressor on PdcmA. | ||
| + | <br><br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/c/c0/Oxford_DCMR_Equations2.png" style="float:left;position:relative; width:35%; margin-right:65%;margin-bottom:2%;margin-left:0%;" /> | ||
| + | |||
| + | |||
| + | Using the analytical solution outlined above, we were then able to characterize the single unknown parameter in the system (β3 - the basal rate of transcription of sfGFP). By again utilizing our data fitting algorithm alongside our hypothetical value for the basal rate of transcription of sfGFP, β3 was calculated to be 4.6. | ||
| + | <br><br> | ||
| + | |||
| + | Now that we know two of the four parameters for the second half of our synthetic circuit (DcmR regulating sfGFP), we needed to calculate the final two parameters to complete our model. To do this, we analysed wet-lab data that showed the system in the presence of DcmR. This now means that the non linear term in our ODE is non zero and the analysis becomes | ||
| + | <br><br> | ||
| + | <h1>Expression rate constant (α3) and Michaelis - Menten constant (k3)</h1> | ||
| + | <br> | ||
| + | This data is shown here. Note the difference in the right hand plot reaffirming that DcmR acts as a repressor on PdcmA. | ||
| + | |||
| + | <br><br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/6/61/Oxford_3withDcmR.jpg" style="float:left;position:relative; width:100%; margin-right:0%;margin-bottom:2%;margin-left:0%;" /> | ||
| + | |||
| + | Similar parameter calculation from this data gives: | ||
| + | <br><br> | ||
| + | <h1>α3 = 0.95 min^-1</h1> | ||
| + | |||
| + | <h1>k3 = 0.065 ml/ng</h1> | ||
| + | |||
| + | <br><br><br><br> | ||
| + | |||
| + | <h1>Using the completed model</h1> | ||
| + | Entering these parameters into the model and comparing the response to data allowed us to analyse how effective our modelling had been. An example of how the model fits with some of the data that we used to derive the parameters is shown below: | ||
| + | <br><br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/c/ca/Oxford_CharacOV4.png" style="float:left;position:relative; width:100%; margin-right:0%;margin-bottom:2%;margin-left:0%;" /> | ||
| + | |||
| + | |||
| + | More on the further use of this model is available in the <a href="https://2014.igem.org/Team:Oxford/biosensor_optimisation">optimisation</a> section. | ||
| + | |||
| + | <br><br> | ||
| + | <h1>Reference</h1> | ||
| + | [1] Andersen JB1, Sternberg C, Poulsen LK, Bjorn SP, Givskov M, Molin S. New unstable variants of green fluorescent protein for studies of transient gene expression in bacteria.(1998) Appl Environ Microbiol. 64(6):2240-6 | ||
</div> | </div> | ||
Latest revision as of 03:44, 18 October 2014


























 "
"








 Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.
Deterministic models are very powerful tools for synthetic biology. They describe the behaviour of the bacteria at the population level and use Ordinary Differential Equations (ODEs) to relate each activation and repression. By constructing a cascade of differential equations one can build a realistic model of the average behaviour of the system.



 Oxford iGEM 2014
Oxford iGEM 2014


















 This simplifies the equation to:
This simplifies the equation to:
 As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
As we want our model to accurately predict the fluorescence, we will substitute the fluorescence value in place of the [DcmR] and rearrange:
 Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:
Substituting in the value for δ1 that we found above and the basal steady state fluorescence level from the data (471 to 3 s.f.) gives the basal transcription rate as:

 alongside the correct inputs:
alongside the correct inputs:
 The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
The graph below shows the model's predictions plotted in the same figure as the data points that the wet-lab team obtained for the system:
 Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:
Plotting the model's output as a by interpolating between the calculated values makes the graph clearer:


 The results clearly show a decrease in sfGFP fluorescence upon addition and expression of dcmR. Therefore we can confidently conclude that DcmR acts as a repressor in both directions for the PdcmA and PdcmR promoter.
The results clearly show a decrease in sfGFP fluorescence upon addition and expression of dcmR. Therefore we can confidently conclude that DcmR acts as a repressor in both directions for the PdcmA and PdcmR promoter.

 For the PdcmR promoter both with and without DcmR:
For the PdcmR promoter both with and without DcmR:
 From these results we can see that in the direction of PdcmA DCM has a modulating effect of relieving DcmR repression thus DCM acts through depression. Interestingly, DCM appears to decrease sfGFP fluorescence in the absence of DcmR.
In the direction of PdcmR DCM appears to have no significant effect on the expression of sfGFP. Therefore in the native system we suggest that DCM has a modulating effect through depression of dcmA expression. Additionally DCM shows no effect on the auto regulation of dcmR expression.
From these results we can see that in the direction of PdcmA DCM has a modulating effect of relieving DcmR repression thus DCM acts through depression. Interestingly, DCM appears to decrease sfGFP fluorescence in the absence of DcmR.
In the direction of PdcmR DCM appears to have no significant effect on the expression of sfGFP. Therefore in the native system we suggest that DCM has a modulating effect through depression of dcmA expression. Additionally DCM shows no effect on the auto regulation of dcmR expression.



 In terms of the modelling equations, this system is equivalent to setting [DcmR] to zero and ensuring that for this scenario, we set β1 = 0 (basal transcription rate of DcmR) . The mathematics below shows how we used the normalised data to find the basal transcription rate of sfGFP. Note how we’re using equation with parameters α3, β3 and k3 because the wet-lab team were able to prove that DcmR acts as a repressor on PdcmA.
In terms of the modelling equations, this system is equivalent to setting [DcmR] to zero and ensuring that for this scenario, we set β1 = 0 (basal transcription rate of DcmR) . The mathematics below shows how we used the normalised data to find the basal transcription rate of sfGFP. Note how we’re using equation with parameters α3, β3 and k3 because the wet-lab team were able to prove that DcmR acts as a repressor on PdcmA.
 Using the analytical solution outlined above, we were then able to characterize the single unknown parameter in the system (β3 - the basal rate of transcription of sfGFP). By again utilizing our data fitting algorithm alongside our hypothetical value for the basal rate of transcription of sfGFP, β3 was calculated to be 4.6.
Using the analytical solution outlined above, we were then able to characterize the single unknown parameter in the system (β3 - the basal rate of transcription of sfGFP). By again utilizing our data fitting algorithm alongside our hypothetical value for the basal rate of transcription of sfGFP, β3 was calculated to be 4.6.
 Similar parameter calculation from this data gives:
Similar parameter calculation from this data gives:
 More on the further use of this model is available in the
More on the further use of this model is available in the 

































