Team:SUSTC-Shenzhen/Modeling
From 2014.igem.org
(→Matlab code) |
|||
| (14 intermediate revisions not shown) | |||
| Line 13: | Line 13: | ||
==Introduction== | ==Introduction== | ||
| - | The project is intended to treat retrovirus diseases. And we take AIDS as an example. In this project, we want to establish a more effective HIV-curing system with less side-effects by integrating CRISPR/Cas9 system into human hemopoietic stem cells, which aims to protect the helper T cells from virus infection. | + | The project is intended to treat retrovirus diseases. And we take AIDS as an example.Currently, no effective HIV vaccine exists. In this project, we want to establish a more effective HIV-curing system with less side-effects by integrating CRISPR/Cas9 system into human hemopoietic stem cells, which aims to protect the helper T cells from virus infection. |
So we want to know how effective the CRISPR/Cas9 system is for HIV. In this model, we discuss about dynamic changes of different cells in a person’s body using Matlab and we can see how the system works. So this model will help us to forecast the future applications of our project. | So we want to know how effective the CRISPR/Cas9 system is for HIV. In this model, we discuss about dynamic changes of different cells in a person’s body using Matlab and we can see how the system works. So this model will help us to forecast the future applications of our project. | ||
| Line 184: | Line 184: | ||
\end{equation} | \end{equation} | ||
</html> | </html> | ||
| - | + | \(f_m\) is also a variable and also has certain randomness. | |
<html> | <html> | ||
\begin{equation} | \begin{equation} | ||
f_m=\xi_1(\frac{N_h}{N_h+N_l}+\xi_2r) | f_m=\xi_1(\frac{N_h}{N_h+N_l}+\xi_2r) | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
\end{equation} | \end{equation} | ||
</html> | </html> | ||
| Line 201: | Line 194: | ||
| - | After long period of being infected by HIV, the virus persists at a relatively stable level and the CD4+ T-cell count gradually falls. This period, during which the patient is asymptomatic, can last many years. In the final stages of the disease, the viral load usually increases rapidly and the CD4+ T-cell count | + | After long period of being infected by HIV, the virus persists at a relatively stable level and the CD4+ T-cell count gradually falls. This period, during which the patient is asymptomatic, can last many years. In the final stages of the disease, the viral load usually increases rapidly and the CD4+ T-cell count decreases to a point at which the immune system fails to provide protection against opportunistic infections. Death usually occurs due to one of these infections. |
According to derivation of the model above, we can get the approximate results as follows by using Matlab on different conditions. | According to derivation of the model above, we can get the approximate results as follows by using Matlab on different conditions. | ||
CRISPR/Cas9 system is introduced into the body, everything will change. | CRISPR/Cas9 system is introduced into the body, everything will change. | ||
| - | === | + | |
| + | For different conditions, we change the values of parameters to suit a given situation. Here are some examples. | ||
| + | |||
| + | ===Condition 1=== | ||
In conditon 1, CRISPR/Cas9 system is introduced into the body at time of "200". As for Fig2.1 to Fig 2.5, the parameters are same. | In conditon 1, CRISPR/Cas9 system is introduced into the body at time of "200". As for Fig2.1 to Fig 2.5, the parameters are same. | ||
| Line 233: | Line 229: | ||
Fig2.5 is partial enlarged view of Fig 2.4. It can help us understand the change. | Fig2.5 is partial enlarged view of Fig 2.4. It can help us understand the change. | ||
| - | === | + | ===Condition 2=== |
Under condition 2, there is no CRISPR/Cas9 system. And the patient didn't take actions to compete with HIV. | Under condition 2, there is no CRISPR/Cas9 system. And the patient didn't take actions to compete with HIV. | ||
| Line 240: | Line 236: | ||
<center>Fig 3. HIV counting versus Time </center> | <center>Fig 3. HIV counting versus Time </center> | ||
| - | As is shown by the Fig 3., the | + | As is shown by the Fig 3., the HIV will reach a very high value and the patient will be very dangerous without the outside help. |
| + | |||
| + | ===Condition 3=== | ||
| + | |||
| + | <center>{{SUSTC-Image|wiki/images/e/eb/SUSTC-Shenzhen-2014-model-021.jpg }}</center> | ||
| + | <center>Fig 4.1 </center> | ||
| + | |||
| + | <center>{{SUSTC-Image|wiki/images/1/16/SUSTC-Shenzhen-2014-model-022.jpg }}</center> | ||
| + | <center>Fig 4.2 </center> | ||
| + | |||
| + | All parameters in Fig 4.1 and Fig 4.2 are the same. The only different between at first is the value of low-resistance T cells counting. If the number of low-resistance T cells is too small, it may increase for a while. | ||
| + | |||
| + | ===Matlab code=== | ||
| + | A simple Matlab code example: https://2014.igem.org/Team:SUSTC-Shenzhen/Modeling/matlabcode | ||
==Results== | ==Results== | ||
| - | If the environment doesn't change, we can stimulate the situation in Matlab for a short time. The result is that the CRISPR/Cas9 system will take effect. | + | The relationship between cells and HIV is too complex that we can't make a model to fit out each situations. But the existence of the parameters enable us to handle most of the situations. If the environment doesn't change, we can stimulate the situation in Matlab for a short time. The result is that the CRISPR/Cas9 system will take effect. A small change may cause the butterfly effect. |
==Reference== | ==Reference== | ||
Latest revision as of 03:59, 18 October 2014
Modeling
The art of mathematics, blended with practice.
Contents |
Introduction
The project is intended to treat retrovirus diseases. And we take AIDS as an example.Currently, no effective HIV vaccine exists. In this project, we want to establish a more effective HIV-curing system with less side-effects by integrating CRISPR/Cas9 system into human hemopoietic stem cells, which aims to protect the helper T cells from virus infection.
So we want to know how effective the CRISPR/Cas9 system is for HIV. In this model, we discuss about dynamic changes of different cells in a person’s body using Matlab and we can see how the system works. So this model will help us to forecast the future applications of our project.
In our model, we can see the influence the CRISPR/Cas system produces by the change of virus and cells. But there are too many parameters and that makes it impossible to get clear relation of these parameters easily. If the environment doesn't change, we can stimulate the situation in Matlab for a short time.
Derivation of the model
Theoretical analysis
First, stably transfect hematopoietic stem cells with the plasmid which encodes Cas9 protein. To make the question easier, we suppose that the efficiency is constant. As is shown in other part in this project, second, we can construct a plasmid which encodes the gRNA sequence which is a 20bp conserved regions in HIV DNA and has no conservation in human genome. When the human body is infected by AIDS, using non-viral DNA transfecting methods (in our project we choose A-B toxin based shuttle) to deliver the plasmid into human somatic cells (especially CD4+ cells) and the CRISPR/Cas system is activated. The Cas9 protein recognizes viral DNA with the help of gRNA and cut the target sequence, causing double strand break (DSB). The DSB is then repaired by the non-homologous end joining mechanism in the cell but with high error rate (in this model we suppose the rate doesn’t change), causing frame-shift mutation and gene knockout. The viral protein synthesis is stopped and further infection is impossible, but it provides potentiation for eradicating AIDS.
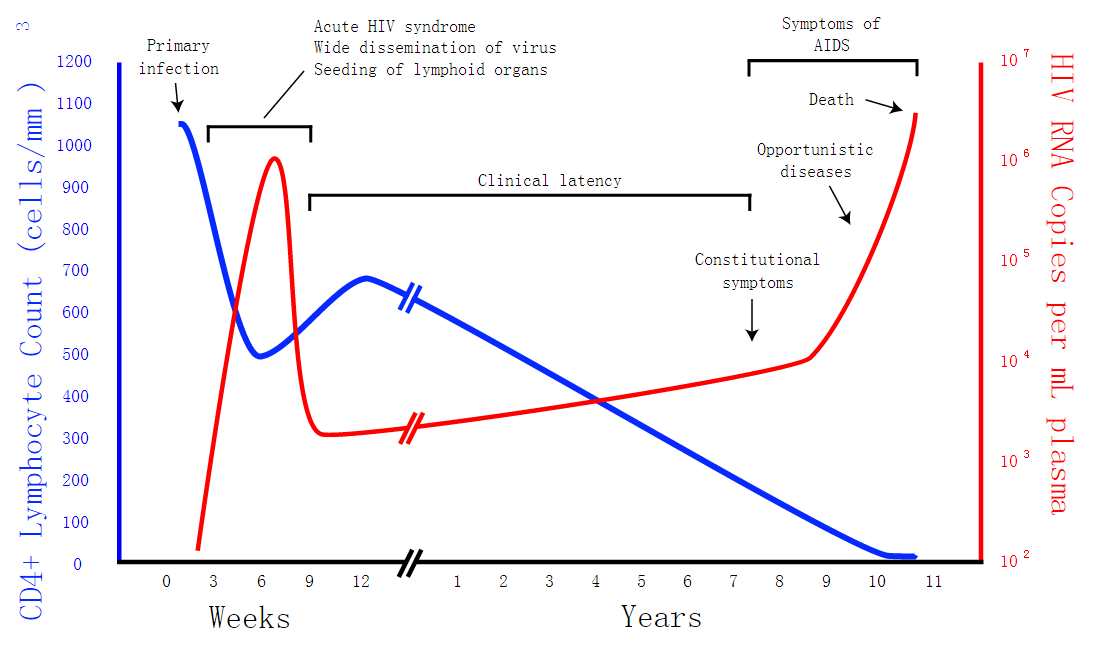
Fig 1 is a generalized graph of the relationship between HIV copies (viral load) and CD4 counts over the average course of untreated HIV infection from Wikipedia. Because any particular individual's disease course may vary considerably.
Symbol description
\(M_{thymus}\) the maximum number of immunological cells
\(N_{thymus}\) the number of immunological cells
\( N_h\) high resistant immune cells number
\( N_l\) low resistant immune cells number
\( P_{thymus}\) the enviroment pressure for immune cell growth
\(P_{hiv}\) almost no self-pressure for hiv virus
\( f_{ht}\) the hiv-caused the number of immunological cells decreasing factor
\( f_{hlh}\) the high and low immune cell induced increasing factor
\(vg_{tg}\) the self-generation rate of stem cell
\(vg_{sh}\) the self-generation rate of hiv virus
\(f_m\) the mutation factor
\(f_{hr}\) the high resistance factor
\(f_{lr}\) the low resistance factor
\(M_{hiv}\) the possible total hiv counting, can be set to be infinity
\(N_{hiv}\) the number of hiv virus
\(vg_{th}\) the generation rate by the number of immunological cells
\(vd_{td}\) the decay(death) rate from high resistant T cell to low ones
\(vg_{lh}\) the gain rate from low resistant T cell to high ones
\(vg_{tl}\) generation rate from the number of immunological cells
\(vd_{hl}\) the death rate caused by hiv virus
\(vg_{gt}\) the gain rate by the immune decaying of high resistant T cells
\(r\) random number between 0 and 1
Formula derivation
We suppose that a person was infected by HIV for some time. And the environment doesn't change in our model. Because the existence of CRISPR/Cas9 system and other environment effects, we can roughly divide the immunological cells into two sides. One is with high resistance, the other is with low resistance.
English letters express variables, while Greek letters express parameters.
HIV infects vital cells in the human immune system such as helper T cells (specifically CD4+ T cells), macrophages, and so on. HIV virus will attract T cells, so we can suppose that there is a linear relationship between the decreasing rate and the number of HIV and we will get equation (1) as follow.
\begin{equation} \frac{{\rm d} N^{(1)}_{thymus}}{{\rm d} t}=-\alpha_1 N_{hiv} \end{equation} Some kinds of immunological cells can replicate, so the increasing rate of immunological cells is influenced by the number of immunological cells. So we will get equation (2) as follow. \begin{equation} \frac{{\rm d} N^{(2)}_{thymus}}{{\rm d} t}=\alpha_2 N_h +\alpha_3 N_l \end{equation} T cells as hosts can boost the increasing of HIV, so we can get equation (3). \begin{equation} \frac{{\rm d} N_{hiv}}{{\rm d} t}=\beta_1 f_m(\beta_2 N_l+\beta_3 N_h) \end{equation} High resistance ones can decrease the number of HIV virus, which implies equation (4). \begin{equation} \frac{{\rm d} N_{hiv}}{{\rm d} t}=\epsilon(1-f_m)N_{hiv}N_h \end{equation} Of course, high resistance ones increase due to T cells' increasing. \begin{equation} \frac{{\rm d} N^{(1)}_{h}}{{\rm d} t}=\delta N_{thymus} \end{equation} HIV virus caused the high ones increasing slower than normal situation. \begin{equation} \frac{{\rm d} N^{(2)}_{h}}{{\rm d} t}=\gamma_1(1-\gamma_2 N_{hiv}) \end{equation} If we combine equation (5) and equation (6), we can get equation (7) as follows. \begin{equation} \frac{{\rm d} N_{h}}{{\rm d} t}=\delta N_{thymus}+\gamma_1(1-\gamma_2 N_{hiv}) \end{equation} Immunity decay rate for high ones due to mutation, which we can express by equation (9). \begin{equation} \frac{{\rm d} vd_{td}}{{\rm d} t}=\eta N_h N_{hiv}e^{\varepsilon f_{hr}} \end{equation} The number of high ones increase due to low ones that enhance the immune capacity. \begin{equation} \frac{{\rm d} N_h}{{\rm d} t}=\zeta N_l e^{ f_{lr}} \end{equation} Because low ones increase due to the number of immunological cells, we can get mathematic relation between the two variables. \begin{equation} \frac{{\rm d} N_l}{{\rm d} t}=\iota N_{thymus} \end{equation} HIV virus caused the high ones increasing slower than normal. \begin{equation} \frac{{\rm d} N_h}{{\rm d} t}=1-\kappa N_{hiv} \end{equation} Cells will die after HIV's attack. death formula for low ones due to HIV virus is as follow. \begin{equation} \frac{{\rm d} N_l}{{\rm d} t}=\lambda N_l N_{hiv} e^{\mu f_{lr}} \end{equation}
The values of parameters will depend on whether there is CRISPR/Cas9 system in the body. And we can change the values of parameters on different environments.
\(N_{thymus}\) changes with the change of time \(t \). \begin{equation} N_{thymus}=\int_{0}^{t}[vg_{tg}M_{thymus}(1-\frac{P_{thymus}N_{thymus}}{M_{thymus}})+f_{ht}\alpha_1 N_{hiv}+f_{hlh}\alpha_2 N_h +\alpha_3 N_l]{{\rm d} t} \end{equation} \(N_{hiv}\) changes with the change of time \(t \). \begin{equation} N_{hiv}=\int_{0}^{t}[vg_{sh}N_{hiv}(1-\frac {N_{hiv}}{M_{hiv}}P_{hiv})\beta_1 f_m(\beta_2 N_l+\beta_3 N_h))-\epsilon(1-f_m)N_{hiv}N_h]{{\rm d} t} \end{equation} \(N_h\) changes with the change of time \(t \). \begin{equation} N_h=\int_{0}^{t}[vg_{th}\delta N_{thymus}\gamma_1(1-\gamma_2 N_{hiv})-vd_{td}\eta N_h N_{hiv}e^{\varepsilon f_hr}+vg_{lh}\zeta N_l e^{ f_{lr}}] {{\rm d} t} \end{equation} \(N_l\) changes with the change of time \(t \). \begin{equation} N_l=\int_{0}^{t}[vg_{tl}\iota N_{thymus}(1-\kappa N_{hiv})-vd_{hl}\lambda N_l N_{hiv} e^{\mu f_{lr}}]{{\rm d} t} \end{equation} \(f_m\) is also a variable and also has certain randomness. \begin{equation} f_m=\xi_1(\frac{N_h}{N_h+N_l}+\xi_2r) \end{equation}
Matlab analysis
After long period of being infected by HIV, the virus persists at a relatively stable level and the CD4+ T-cell count gradually falls. This period, during which the patient is asymptomatic, can last many years. In the final stages of the disease, the viral load usually increases rapidly and the CD4+ T-cell count decreases to a point at which the immune system fails to provide protection against opportunistic infections. Death usually occurs due to one of these infections.
According to derivation of the model above, we can get the approximate results as follows by using Matlab on different conditions. CRISPR/Cas9 system is introduced into the body, everything will change.
For different conditions, we change the values of parameters to suit a given situation. Here are some examples.
Condition 1
In conditon 1, CRISPR/Cas9 system is introduced into the body at time of "200". As for Fig2.1 to Fig 2.5, the parameters are same.
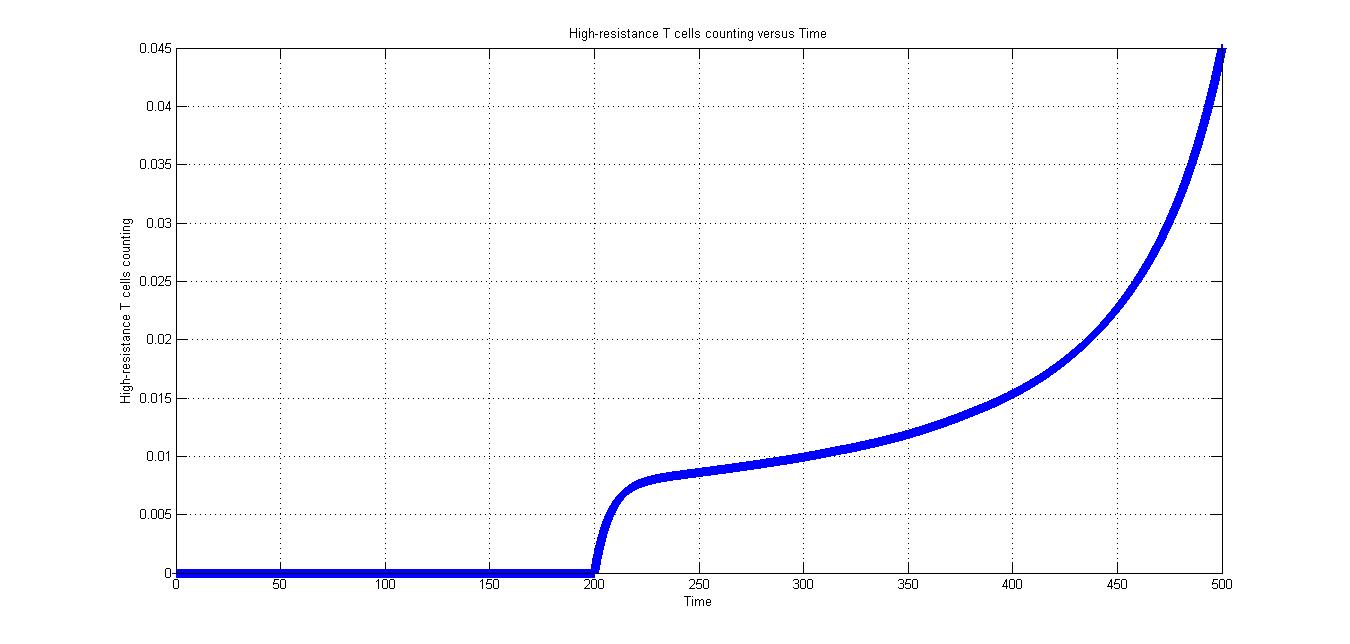
As is shown in Fig2.1, after the CRISPR/Cas9 system introduced in the body, high-resistance T cells appear and increase rapidly.

Fig2.2 shows the low-resistance T cells counting versus time, we can find that low-resistance T cells also increase after the CRISPR/Cas9 system introduced in the body, but it's much slower than that of high-resistance T cells.
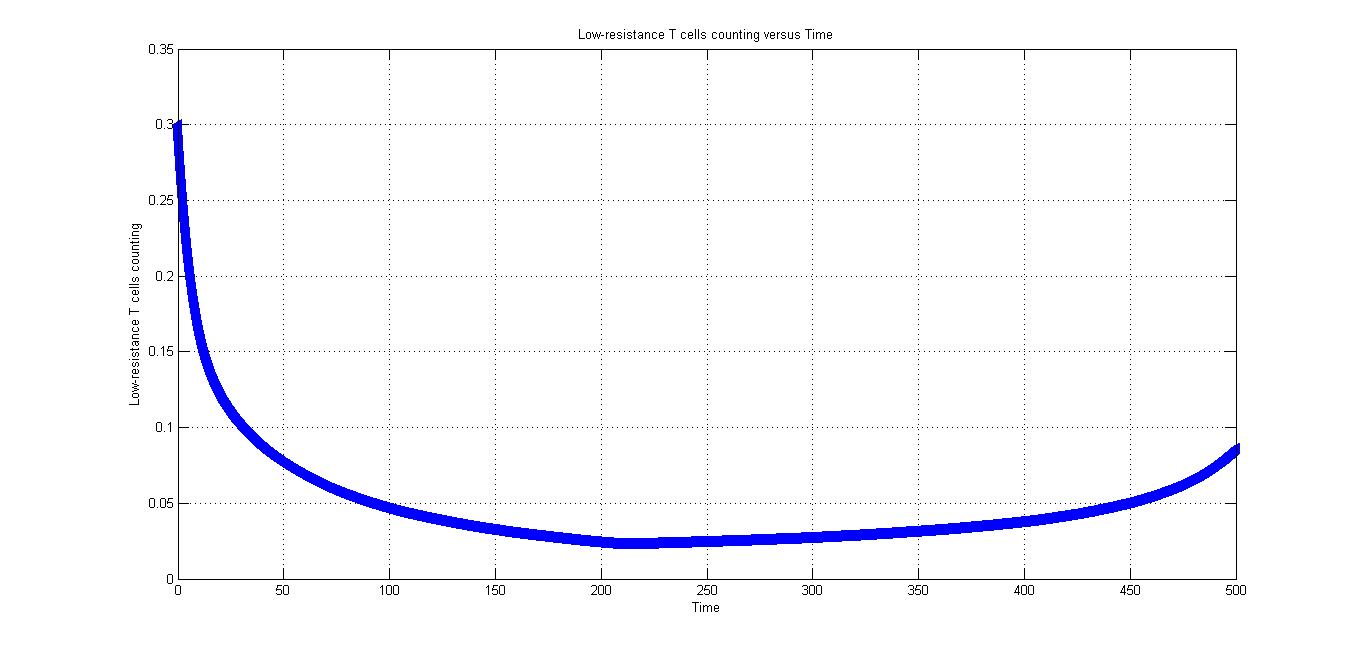
Fig2.3 is partial enlarged view of Fig 2.3. It can help us understand the change about the time of "200".
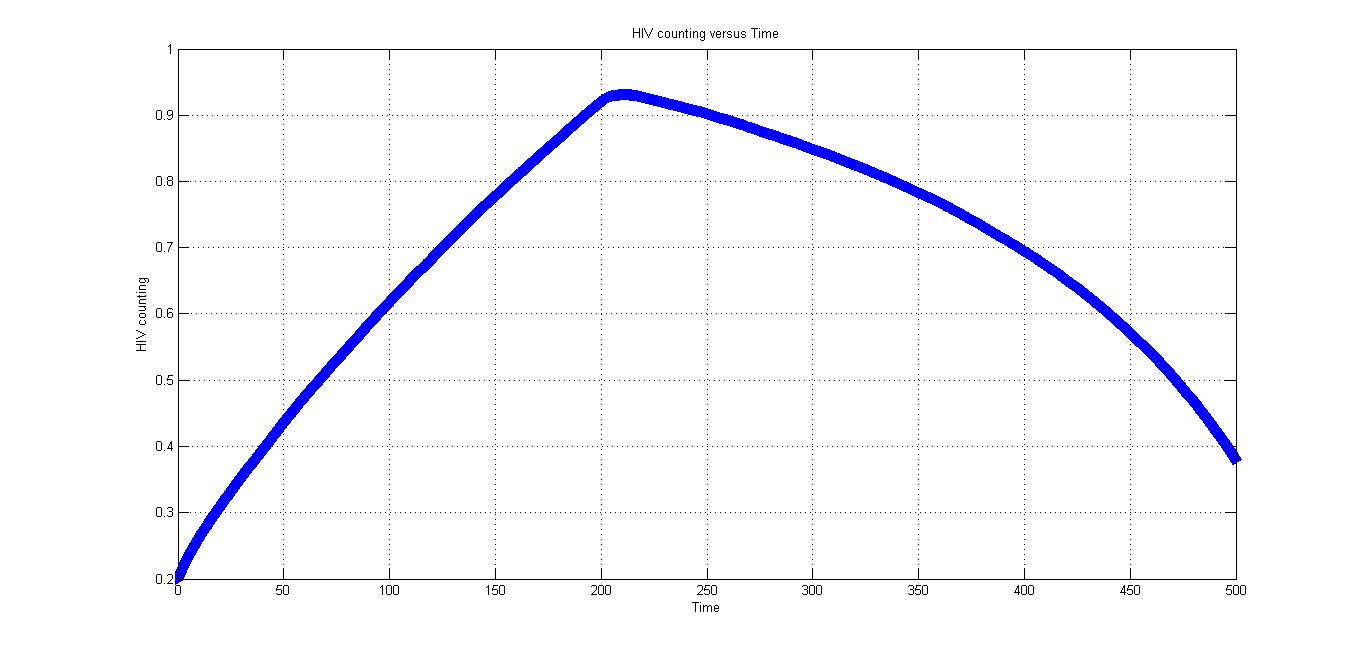
Fig2.4 can roughly describe of change of HIV virus' number. After the CRISPR/Cas9 system introduced in the body, HIV virus decrease.

Fig2.5 is partial enlarged view of Fig 2.4. It can help us understand the change.
Condition 2
Under condition 2, there is no CRISPR/Cas9 system. And the patient didn't take actions to compete with HIV.
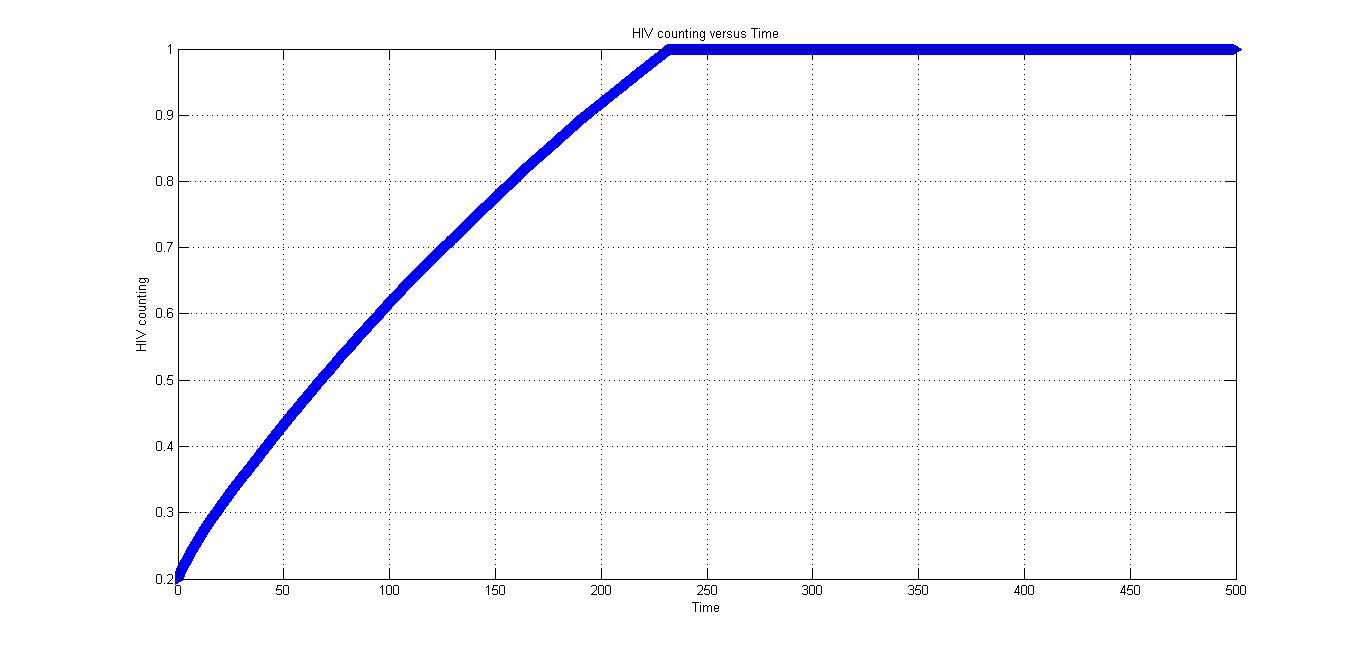
As is shown by the Fig 3., the HIV will reach a very high value and the patient will be very dangerous without the outside help.
Condition 3
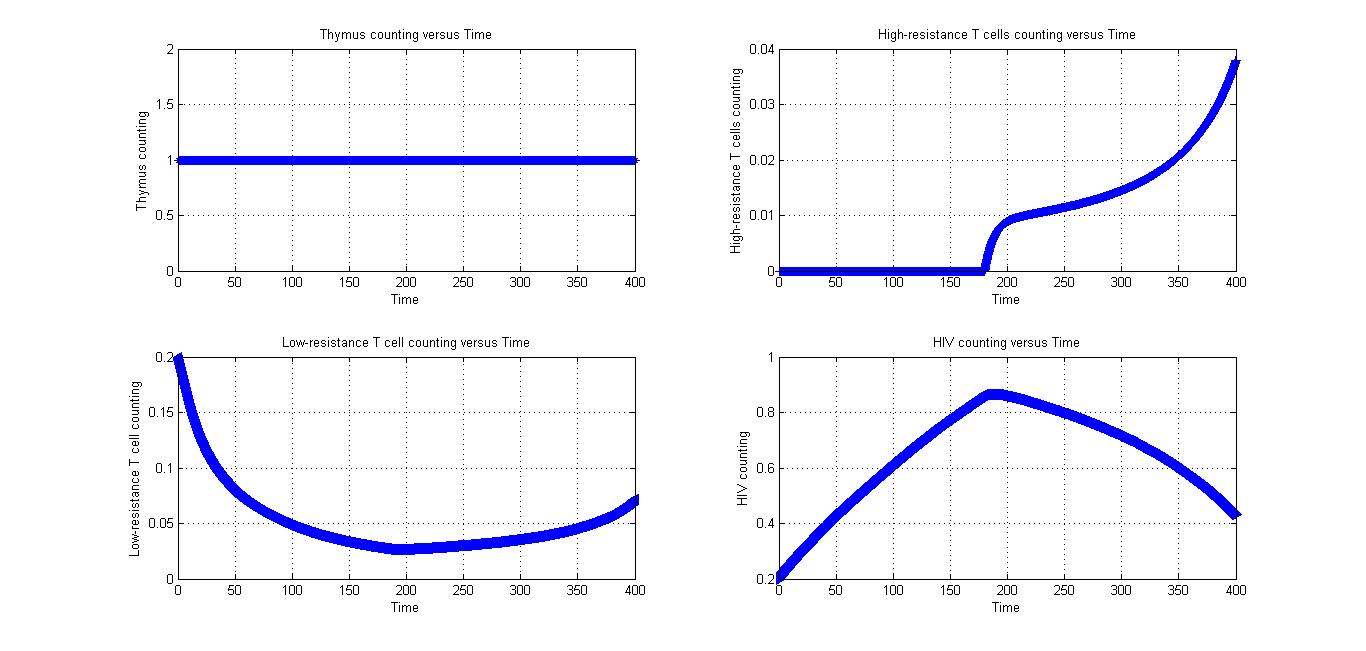
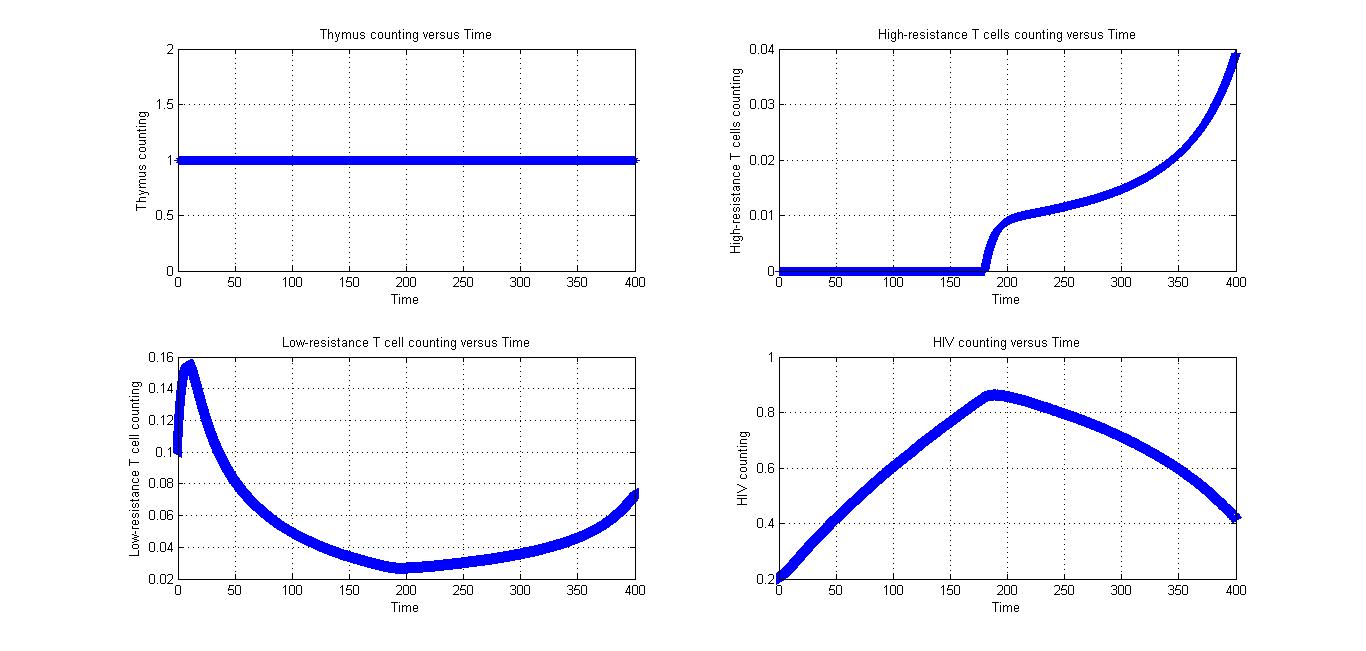
All parameters in Fig 4.1 and Fig 4.2 are the same. The only different between at first is the value of low-resistance T cells counting. If the number of low-resistance T cells is too small, it may increase for a while.
Matlab code
A simple Matlab code example: https://2014.igem.org/Team:SUSTC-Shenzhen/Modeling/matlabcode
Results
The relationship between cells and HIV is too complex that we can't make a model to fit out each situations. But the existence of the parameters enable us to handle most of the situations. If the environment doesn't change, we can stimulate the situation in Matlab for a short time. The result is that the CRISPR/Cas9 system will take effect. A small change may cause the butterfly effect.
Reference
Berezovskaya, F. S., Wolf, Y. I., Koonin, E. V., & Karev, G. P. (2014). Pseudo-chaotic oscillations in CRISPR-virus coevolution predicted by bifurcation analysis. Biology direct, 9(1), 13.
Cunningham, A. L., Donaghy, H., Harman, A. N., Kim, M., & Turville, S. G. (2010). Manipulation of dendritic cell function by viruses. Current opinion in microbiology, 13(4), 524-529.
Cong, L., Ran, F. A., Cox, D., Lin, S. L., Barretto, R., Habib, N., . . . Zhang, F. (2013). Multiplex Genome Engineering Using CRISPR/Cas Systems. Science, 339(6121), 819-823.
Mittler, J. E., Sulzer, B., Neumann, A. U., & Perelson, A. S. (1998). Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Mathematical biosciences, 152(2), 143-163.
"HIV" [Online] Available: http://en.wikipedia.org/wiki/HIV (Sep 17, 2014)
 "
"