Team:Toulouse/Modelling
From 2014.igem.org
| (7 intermediate revisions not shown) | |||
| Line 116: | Line 116: | ||
<div class="fils-ariane" style="width:100%; height:60px; background:#ededed;"> | <div class="fils-ariane" style="width:100%; height:60px; background:#ededed;"> | ||
| - | <p style="margin:0 auto; color:#696969; width:960px; padding-top:20px; font-size:16px;"> | + | <p style="margin:0 auto; color:#696969; width:960px; padding-top:20px; font-size:16px;">Results > Modeling |
</div> | </div> | ||
| Line 125: | Line 125: | ||
<p class="texte"> | <p class="texte"> | ||
| - | Modeling is a tool used to simplify and study systems. It helps us to predict behavior | + | Modeling is a tool used to simplify and study systems. It helps us to predict behavior of biological systems using bibliographic or experimental data.</br> |
| - | The following modelisation focuses on the development of | + | The following modelisation focuses on the development of a bacterium in trees. The bacterial growth in trees seems to be unknown, thus we must infer <i>Bacillus subtilis'</i> behavior.</p> |
<p class="title1"> | <p class="title1"> | ||
| Line 138: | Line 138: | ||
<p class="texte"> | <p class="texte"> | ||
| - | <i>Bacillus subtilis</i> is a tree endophyte strain. A study showed that <i> | + | <i>Bacillus subtilis</i> is a tree endophyte strain. A study showed that <i>B. subtilis</i> could develop and fully colonize a tree, reaching a concentration of 10<sup>5</sup> cells per gram of fresh plant. We need to know in which conditions the growth of <i>B. subtilis</i> is optimum in a tree and if the weather can stop its development during winter. Therefore we decided to work on the growthof <i>B. subtilis'</i> in function of the temperature during the year. |
| - | <br>Modeling bacterial growth in a tree section generates some difficulties. We need to know the distance between two tree extremities (treetops and root) or the speed sap flow. However the speed sap | + | <br>Modeling bacterial growth in a tree section generates some difficulties. We need to know the distance between two tree extremities (treetops and root) or the speed sap flow. However the flow of speed sap can vary with temperature during the day. The composition of sap also varies due to seasons and type of container (phloem, xylem). Furthermore a tree is not an homogeneous system: its roots, trunk and branches do not contain the same amount of sap and wood. <br>The average speed of the plane tree sap is 2.4 m/h, which means that in a day the sap of a 30 m tree will flow from one extremity to the other. We thus reduced the tree to a bioreactor. |
</p> | </p> | ||
<p class="texte"> | <p class="texte"> | ||
| Line 145: | Line 145: | ||
<ol class="list1"> | <ol class="list1"> | ||
<li> | <li> | ||
| - | According to the publication of <b>Xianling Ji</b> (See References), after six months of <i> | + | According to the publication of <b>Xianling Ji</b> (See References), after six months of <i>B. subtilis</i> growth in a tree, bacteria cells reach a concentration of 10<sup>5</sup> cells per gram of fresh plant. We assume that 10<sup>5</sup> cells/g is the maximum concentration. |
</li> | </li> | ||
<li> | <li> | ||
| Line 154: | Line 154: | ||
</li> | </li> | ||
<li> | <li> | ||
| - | It is | + | It is assumed that there is no leakage of cells. |
</li> | </li> | ||
</ol> | </ol> | ||
| Line 164: | Line 164: | ||
<p class="texte"> | <p class="texte"> | ||
| - | An assessment of the <i> | + | An assessment of the <i>B. subtilis</i> growth in a similar sap was performed in laboratory conditions with optimum growth medium for <i>B. subtilis</i>. The composition sap used was the one from birch sap.<br> |
| - | In these conditions, the growth rate | + | In these conditions, the growth rate µ is optimal. From this value we can extrapolate a growth curve as a function of temperature. We used the <b>cardinal temperature model</b>: </p> |
<center style="margin-bottom:50px;"><img style="" src="https://static.igem.org/mediawiki/2014/8/85/Formules_Rosso.png" alt="cardinal temperature model"></center> | <center style="margin-bottom:50px;"><img style="" src="https://static.igem.org/mediawiki/2014/8/85/Formules_Rosso.png" alt="cardinal temperature model"></center> | ||
| Line 186: | Line 186: | ||
The optimal growth rate (µ<sub>opt</sub>) is obtained experimentally with a similar birch sap environment.</br> | The optimal growth rate (µ<sub>opt</sub>) is obtained experimentally with a similar birch sap environment.</br> | ||
| - | The growth rate is negative below 10°C (according to growth tests performed at 10°C and 4°C under similar conditions for the measurement of | + | The growth rate is negative below 10°C (according to growth tests performed at 10°C and 4°C under similar conditions for the measurement of µ<sub>opt</sub>), survival rate after 24h was 0.3 % at 10°C and null at 4°C.<br> |
| - | Conditions | + | Conditions applied:</p> |
<p class="texte"> | <p class="texte"> | ||
| Line 195: | Line 195: | ||
<center style="margin-top: -52px;"><img style="" src="https://static.igem.org/mediawiki/2014/b/b1/Plot_growth_rate.png" alt="Figure1"></center> | <center style="margin-top: -52px;"><img style="" src="https://static.igem.org/mediawiki/2014/b/b1/Plot_growth_rate.png" alt="Figure1"></center> | ||
| - | <p class="legend">Figure 1: | + | <p class="legend">Figure 1: Bacterial growth (µ) as a function of temperature</p> |
<p class="texte"> A logistic model developed by <b>Hiroshi Fujikawa</b> (See References) is used to study bacterial growth.</p> | <p class="texte"> A logistic model developed by <b>Hiroshi Fujikawa</b> (See References) is used to study bacterial growth.</p> | ||
| Line 210: | Line 210: | ||
<br> | <br> | ||
<br>N<sub>min</sub> is slightly lower than N<sub>0</sub>. When N is small at the initial state (N = N<sub>0</sub>) <i>i.e.</i> N is close to N<sub>min</sub>, N<sub>min</sub>/N is almost equal to 1. Therefore the term (1-(N<sub>min</sub>/N)) is nearly 0 and the growth is very slow. | <br>N<sub>min</sub> is slightly lower than N<sub>0</sub>. When N is small at the initial state (N = N<sub>0</sub>) <i>i.e.</i> N is close to N<sub>min</sub>, N<sub>min</sub>/N is almost equal to 1. Therefore the term (1-(N<sub>min</sub>/N)) is nearly 0 and the growth is very slow. | ||
| - | <br>If N | + | <br>If N decreases until it reaches N<sub>min</sub>, the term (1-(N<sub>min</sub>/N)) is equal to 0. Therefore the growth is null. |
| - | <br> Similarly when N is equal to N<sub>max</sub> the term (1-(N/N<sub>max</sub>)) is equal to 0 and the growth is blocked.</br> | + | <br> Similarly when N is equal to N<sub>max</sub>, the term (1-(N/N<sub>max</sub>)) is equal to 0 and the growth is blocked.</br> |
| - | To overcome this we worked under two conditions: positive and negative growth. Theses conditions can be translated in two equations. This | + | To overcome this, we worked under two conditions: positive and negative growth. Theses conditions can be translated in two equations. This leads to the writing of this model:</p> |
<center style="margin: 65px 0;"><img style="" src="https://static.igem.org/mediawiki/2014/f/f8/Form_part.png" alt="model"></center> | <center style="margin: 65px 0;"><img style="" src="https://static.igem.org/mediawiki/2014/f/f8/Form_part.png" alt="model"></center> | ||
| Line 223: | Line 223: | ||
The term (1-(Nmin/N)) is not taken into account when there is growth. <br>The term (1-(N/Nmax)) is not taken into account when there is bacterial decay.</br> | The term (1-(Nmin/N)) is not taken into account when there is growth. <br>The term (1-(N/Nmax)) is not taken into account when there is bacterial decay.</br> | ||
| - | Meteorological records of the Toulouse region during the years 2011-2013 are used to | + | Meteorological records of the Toulouse region during the years 2011-2013 are used to calculate average daily temperatures. Thus we can determine <i>B. subtilis</i> growth in a tree located in Toulouse during a year. This values are obtained for each day by the average on the highest and the lowest temperature. |
</br> | </br> | ||
| - | The density of green wood plane is about | + | The density of green wood plane is about 650 kg/m³. The average diameter of the trunks of the concerned trees is about 0.80 m and they are 15 m high. This represents a volume of 30 m³. Therefore the weight of the trunk is 19.604 kg. |
We need to add to this weight the weight of branches, twigs, about 25% of leaves and about 15% of roots (<a href="http://www.guichetdusavoir.org/viewtopic.php?t=25895">source-FR</a>). | We need to add to this weight the weight of branches, twigs, about 25% of leaves and about 15% of roots (<a href="http://www.guichetdusavoir.org/viewtopic.php?t=25895">source-FR</a>). | ||
</br> | </br> | ||
<!--pas compris ces deux dernières phrases--> | <!--pas compris ces deux dernières phrases--> | ||
| - | The average weight of a tree plane is 27,446kg. We inoculated | + | The average weight of a tree plane is 27,446kg. We inoculated 10 mL of bacterial culture at 10<sup>9</sup>cfu/mL, <i>i.e.</i> 10<sup>10</sup> bacterial cells. This represents 3.64x10<sup>2</sup>cfu/g of fresh plant (N0). |
</p> | </p> | ||
| Line 237: | Line 237: | ||
<p class="texte"> | <p class="texte"> | ||
| - | In our model, growth starts only from 10°C, which happens between March and April. This period seems to be suitable to | + | In our model, growth starts only from 10°C, which happens between March and April. This period seems to be the most suitable to administer the strain in the tree. Starting in December the temperature decreases below 4°C, corresponding to the threshold below which bacteria starts to die. |
</p> | </p> | ||
| Line 245: | Line 245: | ||
<p class="texte"> | <p class="texte"> | ||
| - | In practice, temperature variations are certainly lower in | + | In practice, temperature variations are certainly lower in trees than outside, especially if roots extend very deep. Composition of the tree sap must also intervene in the growth rate and nutrient content of sap is also temperature dependent. The effects of the decrease of the temperature in winter also induces a fall of the sap and this must also be involved in the disappearance of our strain in the tree. The period of <i>B. subtilis</i> growth is certainly affected by the change of temperature, the rise of sap in the trunk and sap composition variations. All these parameters can consequently slow-down or boost the growth rate. |
The modeling work is done with the programming language 'R' script attached (See Annexe). | The modeling work is done with the programming language 'R' script attached (See Annexe). | ||
| Line 257: | Line 257: | ||
<ul> | <ul> | ||
<li class="tree"><p class="texte"> | <li class="tree"><p class="texte"> | ||
| - | Xianling Ji, Guobing Lu, Yingping Gai, Chengchao Zheng | + | Xianling Ji, Guobing Lu, Yingping Gai, Chengchao Zheng,and Zhimei Mu. (2008) <b>Biological control against bacterial wilt and colonization of mulberry by an endophytic <i>Bacillus subtilis</i> strain.</b> FEMS Microbiol Ecol 65: 565–573. |
</li></p> | </li></p> | ||
<li class="tree"><p class="texte"> | <li class="tree"><p class="texte"> | ||
| - | A. Garnier(1977) <b>Transfert de sève brute dans le tronc des arbres aspects méthodologiques et physiologiques.</b> Ann. Sci. Foresi. 34 (1): 17-45 | + | A. Garnier. (1977) <b>Transfert de sève brute dans le tronc des arbres aspects méthodologiques et physiologiques.</b> Ann. Sci. Foresi. 34 (1): 17-45. |
</li></p> | </li></p> | ||
<li class="tree"><p class="texte"> | <li class="tree"><p class="texte"> | ||
| - | Heikki Kallio , Tuija Teerinen , Seija Ahtonen , Meri Suihko , Reino R. Linko (1989) <b>Composition and properties of birch syrup (Betula pubescens).</b> J. Agric. Food Chem 37 (1): 51–54 | + | Heikki Kallio, Tuija Teerinen, Seija Ahtonen, Meri Suihko, and Reino R. Linko. (1989) <b>Composition and properties of birch syrup (<i>Betula pubescens</i>).</b> J. Agric. Food Chem 37 (1): 51–54. |
</li></p> | </li></p> | ||
<li class="tree"><p class="texte"> | <li class="tree"><p class="texte"> | ||
| - | L. Rosso, J. R. Lobry | + | L. Rosso, J. R. Lobry, and J. P. Flandrois. (1992) AN <b>Unexpected Correlation between Cardinal Temperatures of Microbial Growth Highlighted by a New Model.</b> J. theor. Biol. 162 : 447-463. |
</li></p> | </li></p> | ||
<li class="tree"><p class="texte"> | <li class="tree"><p class="texte"> | ||
| - | Hiroshi Fujikawa (2010) | + | Hiroshi Fujikawa. (2010) <b>Development of a New Logistic Model for Microbial Growth in Foods.</b> Biocontrol of Science Vol 15: 75-80. |
</li></p> | </li></p> | ||
</ul> | </ul> | ||
| Line 277: | Line 277: | ||
</p> | </p> | ||
| - | <p class="texte"> To | + | <p class="texte"> To download the script and the table <a href="https://static.igem.org/mediawiki/2014/0/01/Annexes.zip">Click Here</a></p> |
| Line 286: | Line 286: | ||
<div class="page-nav" style="border-top:1px solid #cccccc; padding-top:40px; margin-top:40px;"> | <div class="page-nav" style="border-top:1px solid #cccccc; padding-top:40px; margin-top:40px;"> | ||
| - | <a href="https://2014.igem.org/Team:Toulouse/ | + | <a href="https://2014.igem.org/Team:Toulouse/Result/experimental-results" class="page-nav-right" style="width:447px; float:left; display:block;text-decoration:none; color:#666; font-size:18px;">Experimental results |
<img src="https://static.igem.org/mediawiki/2014/2/26/Template-igem2014-img-arrowleft.png" style="display:block; padding-top:10px;"/> | <img src="https://static.igem.org/mediawiki/2014/2/26/Template-igem2014-img-arrowleft.png" style="display:block; padding-top:10px;"/> | ||
</a> | </a> | ||
| Line 300: | Line 300: | ||
</div> | </div> | ||
| - | + | <div class="page-nav-center" style="width:65px; float:left;"> | |
| + | </div> | ||
| + | |||
| + | <a href="https://2014.igem.org/Team:Toulouse/Result/parts" class="page-nav-left" style="width:447px; float:right; display:block; text-align:right; text-decoration:none; | ||
| + | color:#666; font-size:18px;">Parts</br> | ||
| + | <img src="https://static.igem.org/mediawiki/2014/e/ea/Template-igem2014-img-arrowright.png" style="display:block; float:right; padding-top:10px; " /> | ||
| + | </a> | ||
| + | |||
| + | <div class="clear"></div> | ||
</div> | </div> | ||
Latest revision as of 03:17, 18 October 2014
Modeling
To develop a predictive model
Results > Modeling
Modeling is a tool used to simplify and study systems. It helps us to predict behavior of biological systems using bibliographic or experimental data. The following modelisation focuses on the development of a bacterium in trees. The bacterial growth in trees seems to be unknown, thus we must infer Bacillus subtilis' behavior.
Bacterial Growth
Aim
Bacillus subtilis is a tree endophyte strain. A study showed that B. subtilis could develop and fully colonize a tree, reaching a concentration of 105 cells per gram of fresh plant. We need to know in which conditions the growth of B. subtilis is optimum in a tree and if the weather can stop its development during winter. Therefore we decided to work on the growthof B. subtilis' in function of the temperature during the year.
Modeling bacterial growth in a tree section generates some difficulties. We need to know the distance between two tree extremities (treetops and root) or the speed sap flow. However the flow of speed sap can vary with temperature during the day. The composition of sap also varies due to seasons and type of container (phloem, xylem). Furthermore a tree is not an homogeneous system: its roots, trunk and branches do not contain the same amount of sap and wood.
The average speed of the plane tree sap is 2.4 m/h, which means that in a day the sap of a 30 m tree will flow from one extremity to the other. We thus reduced the tree to a bioreactor.
We make the following hypothesis:
- According to the publication of Xianling Ji (See References), after six months of B. subtilis growth in a tree, bacteria cells reach a concentration of 105 cells per gram of fresh plant. We assume that 105 cells/g is the maximum concentration.
- The composition of the phloem is stable. There is no effect of depletion of the medium.
- Only temperature impacts on bacterial growth.
- It is assumed that there is no leakage of cells.
Method
An assessment of the B. subtilis growth in a similar sap was performed in laboratory conditions with optimum growth medium for B. subtilis. The composition sap used was the one from birch sap.
In these conditions, the growth rate µ is optimal. From this value we can extrapolate a growth curve as a function of temperature. We used the cardinal temperature model:

T: Temperature
µopt: Optimal growth rate
µ: growth rate at temperature T
Tmax: Maximum temperature supported by bacteria
Tmin: Minimum temperature supported by bacteria
Topt: Optimum temperature for the growth
Necessary parameters for this function are minimun temperature Tmin and maximum temperature Tmax, optimal temperature for the growth Topt and optimal growth rate µopt.
Tmin: 10°C
Tmax: 52°C
Topt: 37°C
µopt: 8.5968 cfu/d
The optimal growth rate (µopt) is obtained experimentally with a similar birch sap environment.
The growth rate is negative below 10°C (according to growth tests performed at 10°C and 4°C under similar conditions for the measurement of µopt), survival rate after 24h was 0.3 % at 10°C and null at 4°C.
Conditions applied:
If__| T<= 4°C -> µ = -1
____| 4°C
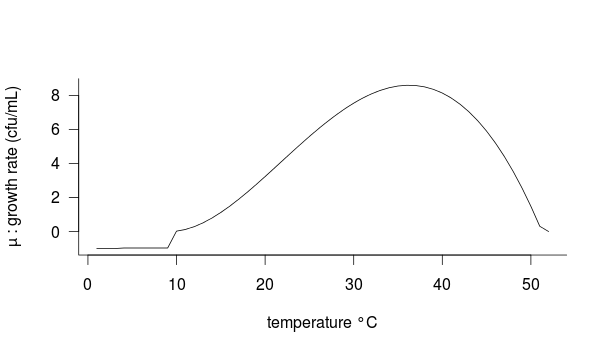
Figure 1: Bacterial growth (µ) as a function of temperature
A logistic model developed by Hiroshi Fujikawa (See References) is used to study bacterial growth.
General logistics formulas:

In our case, the growth rate µ depends on the temperature.
N corresponds to the bacterial population, Nmin and Nmax are two asymptotes.
The parameter m is a curvature parameter. Larger m is, smaller is the curvature of the deceleration phase with the model.
The parameter n is a parameter related to the period lag. Larger n is, shorter is the period of lag.
Nmin is slightly lower than N0. When N is small at the initial state (N = N0) i.e. N is close to Nmin, Nmin/N is almost equal to 1. Therefore the term (1-(Nmin/N)) is nearly 0 and the growth is very slow.
If N decreases until it reaches Nmin, the term (1-(Nmin/N)) is equal to 0. Therefore the growth is null.
Similarly when N is equal to Nmax, the term (1-(N/Nmax)) is equal to 0 and the growth is blocked.
To overcome this, we worked under two conditions: positive and negative growth. Theses conditions can be translated in two equations. This leads to the writing of this model:

with n = 1 and m = 0.5
The term (1-(Nmin/N)) is not taken into account when there is growth.
The term (1-(N/Nmax)) is not taken into account when there is bacterial decay.
Meteorological records of the Toulouse region during the years 2011-2013 are used to calculate average daily temperatures. Thus we can determine B. subtilis growth in a tree located in Toulouse during a year. This values are obtained for each day by the average on the highest and the lowest temperature.
The density of green wood plane is about 650 kg/m³. The average diameter of the trunks of the concerned trees is about 0.80 m and they are 15 m high. This represents a volume of 30 m³. Therefore the weight of the trunk is 19.604 kg.
We need to add to this weight the weight of branches, twigs, about 25% of leaves and about 15% of roots (source-FR).
The average weight of a tree plane is 27,446kg. We inoculated 10 mL of bacterial culture at 109cfu/mL, i.e. 1010 bacterial cells. This represents 3.64x102cfu/g of fresh plant (N0).

Figure 2: (black) Bacillus subtilis growth curve during one year (N is cell quantity by g of fresh plant). (red) average temperature. (blue) threshold at 10°C.
In our model, growth starts only from 10°C, which happens between March and April. This period seems to be the most suitable to administer the strain in the tree. Starting in December the temperature decreases below 4°C, corresponding to the threshold below which bacteria starts to die.
Discussion
In practice, temperature variations are certainly lower in trees than outside, especially if roots extend very deep. Composition of the tree sap must also intervene in the growth rate and nutrient content of sap is also temperature dependent. The effects of the decrease of the temperature in winter also induces a fall of the sap and this must also be involved in the disappearance of our strain in the tree. The period of B. subtilis growth is certainly affected by the change of temperature, the rise of sap in the trunk and sap composition variations. All these parameters can consequently slow-down or boost the growth rate. The modeling work is done with the programming language 'R' script attached (See Annexe).
References
Xianling Ji, Guobing Lu, Yingping Gai, Chengchao Zheng,and Zhimei Mu. (2008) Biological control against bacterial wilt and colonization of mulberry by an endophytic Bacillus subtilis strain. FEMS Microbiol Ecol 65: 565–573.
A. Garnier. (1977) Transfert de sève brute dans le tronc des arbres aspects méthodologiques et physiologiques. Ann. Sci. Foresi. 34 (1): 17-45.
Heikki Kallio, Tuija Teerinen, Seija Ahtonen, Meri Suihko, and Reino R. Linko. (1989) Composition and properties of birch syrup (Betula pubescens). J. Agric. Food Chem 37 (1): 51–54.
L. Rosso, J. R. Lobry, and J. P. Flandrois. (1992) AN Unexpected Correlation between Cardinal Temperatures of Microbial Growth Highlighted by a New Model. J. theor. Biol. 162 : 447-463.
Hiroshi Fujikawa. (2010) Development of a New Logistic Model for Microbial Growth in Foods. Biocontrol of Science Vol 15: 75-80.
Annexe
To download the script and the table Click Here

 "
"



