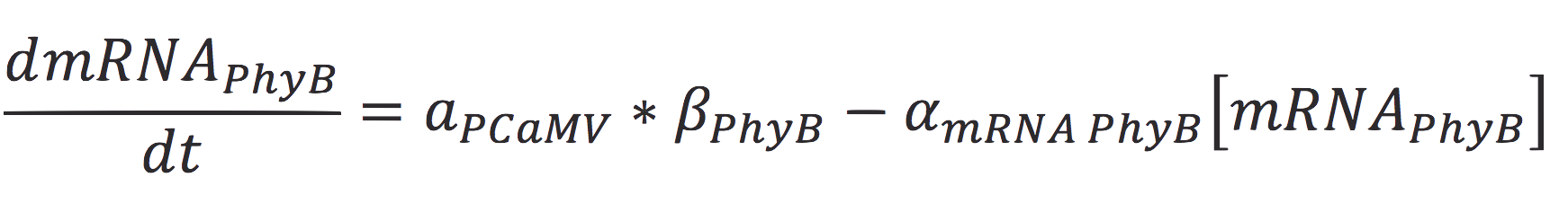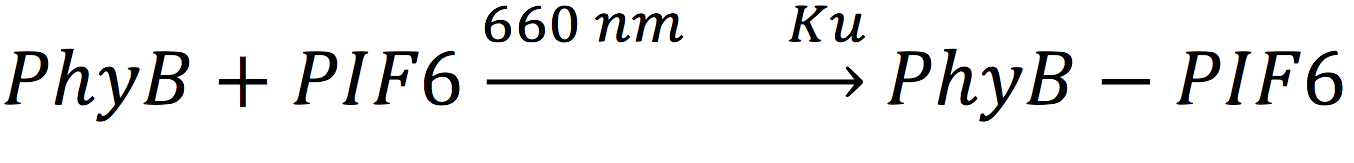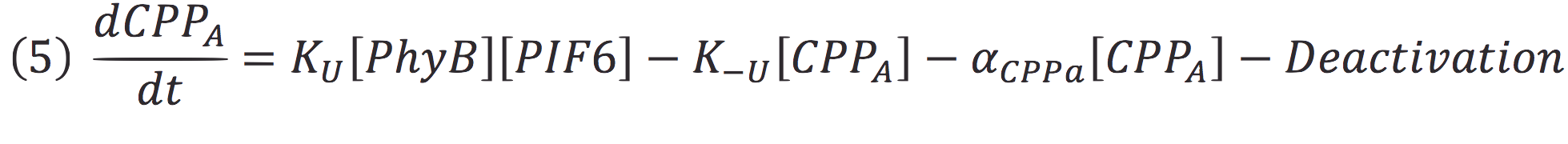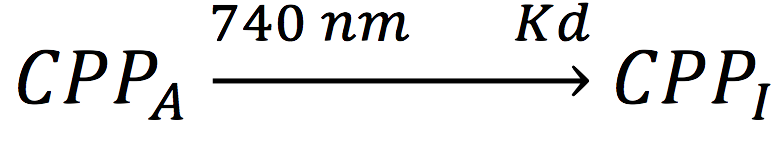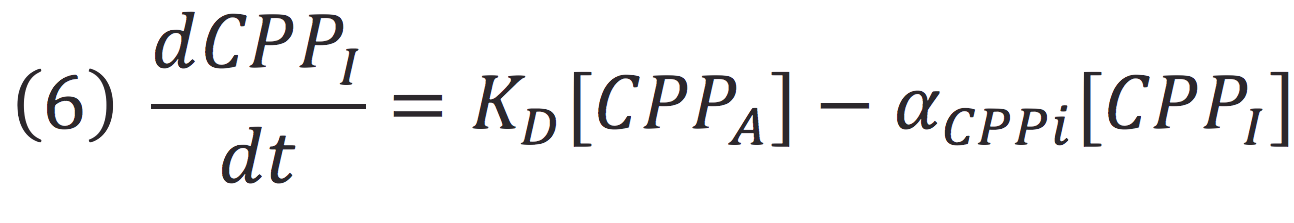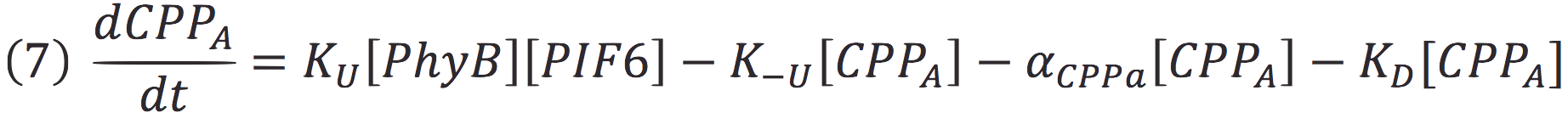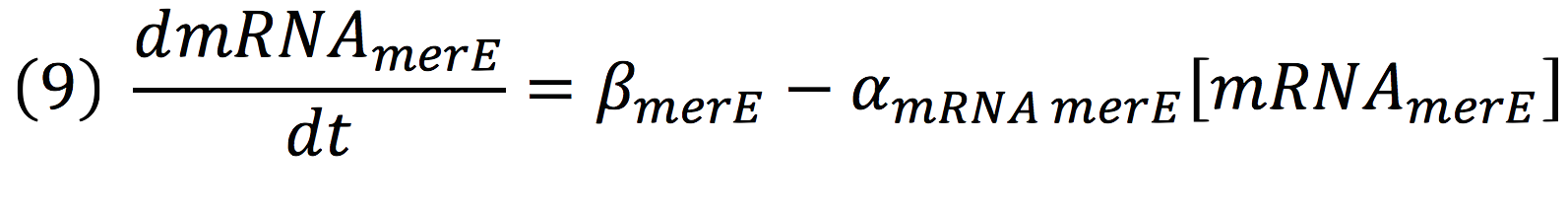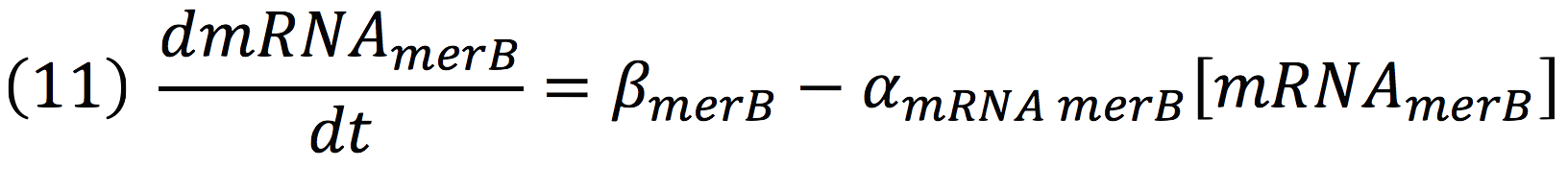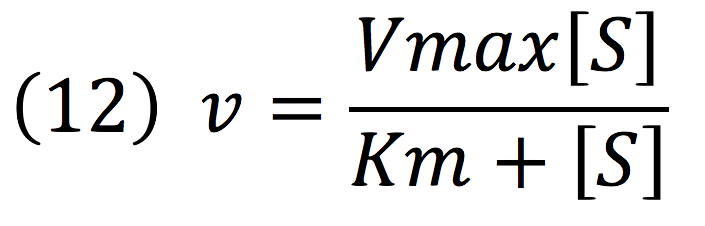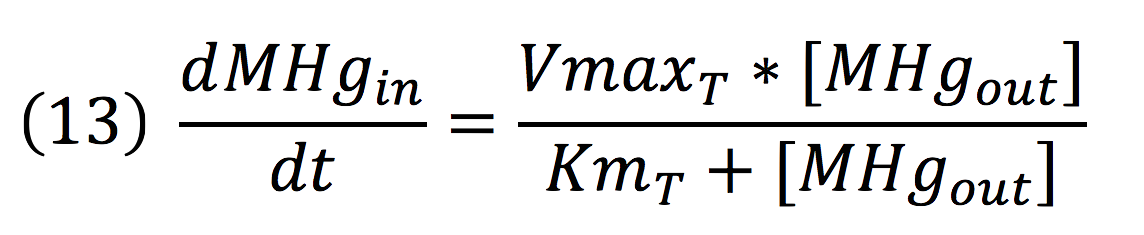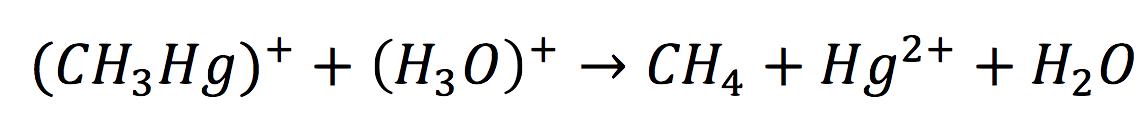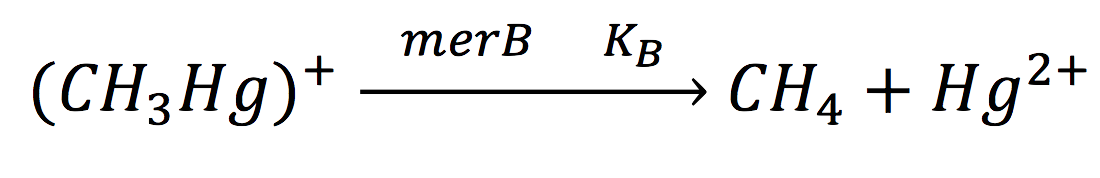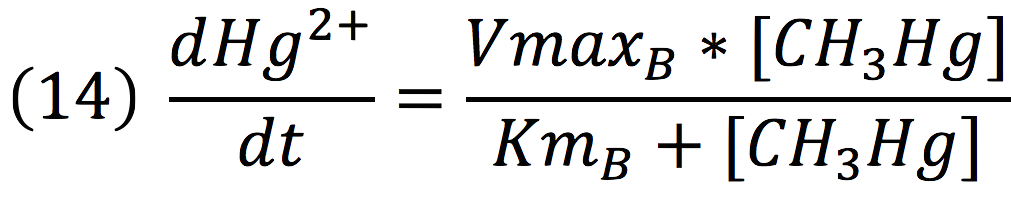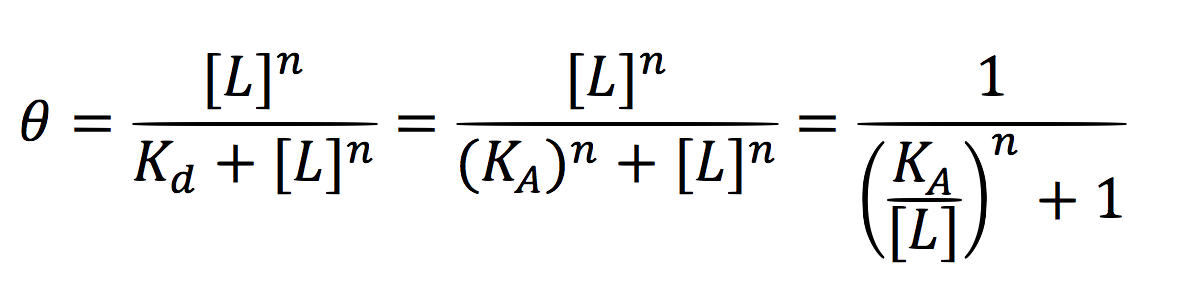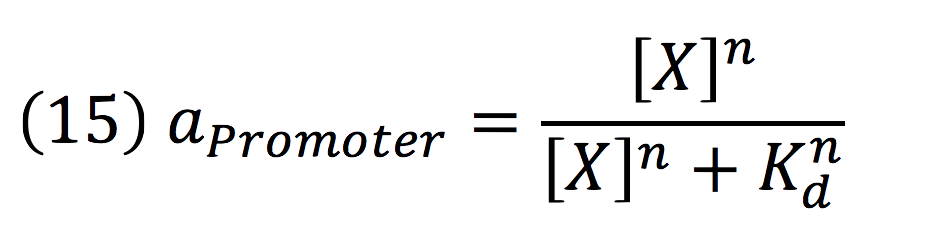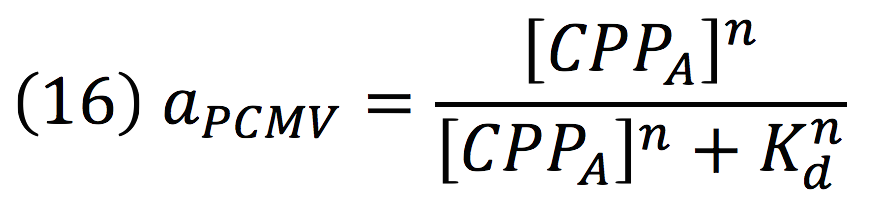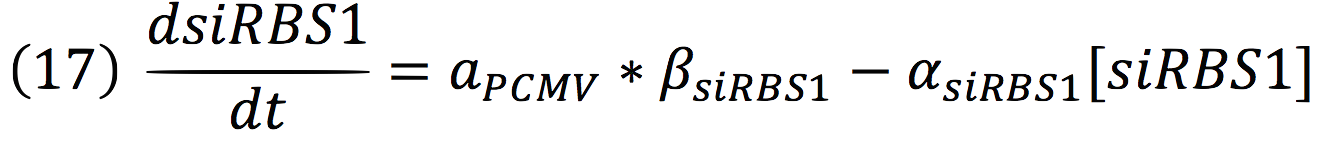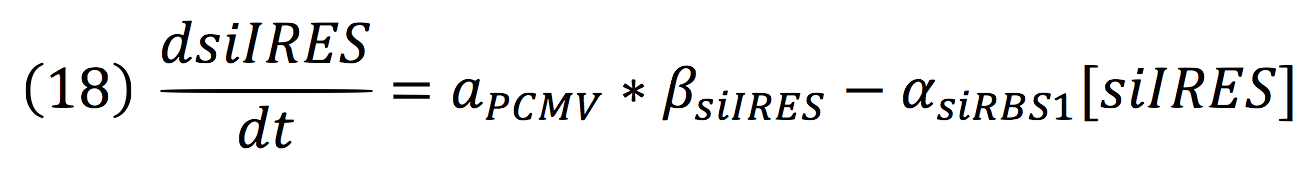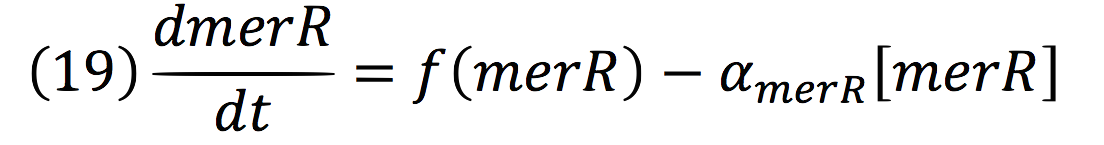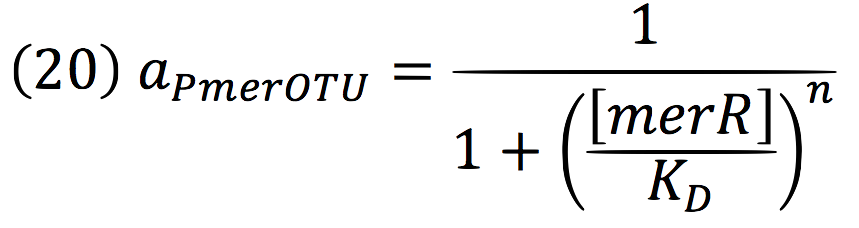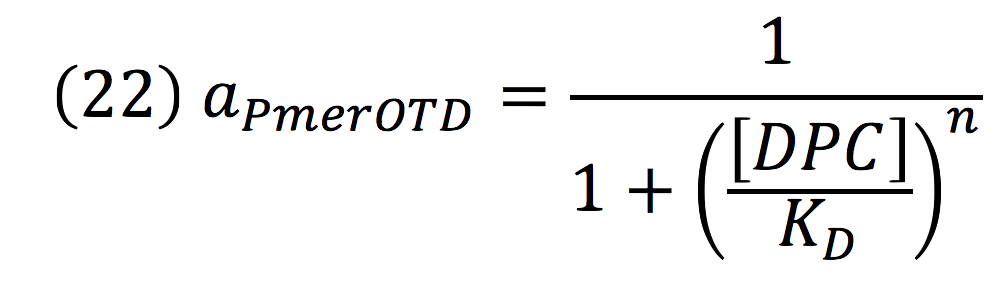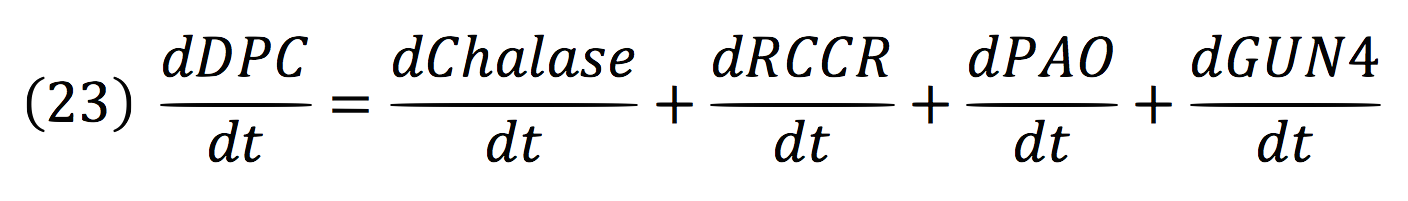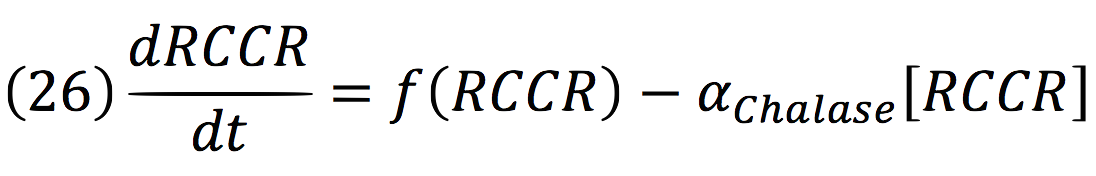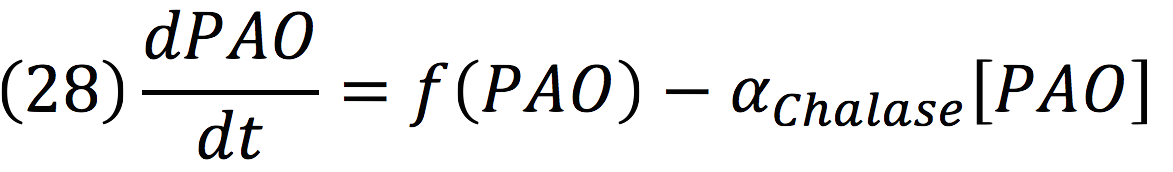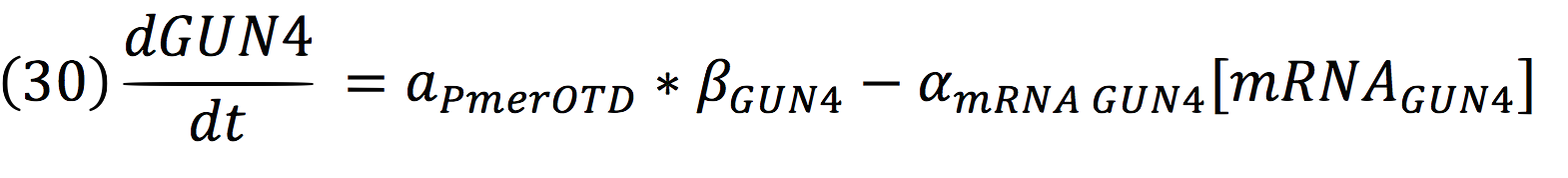Team:BIOSINT Mexico/Modeling
From 2014.igem.org
JuanjoQuispe (Talk | contribs) |
|||
| (6 intermediate revisions not shown) | |||
| Line 8: | Line 8: | ||
</style> | </style> | ||
</html> | </html> | ||
| - | [[File: | + | [[File:BSMexMODELING2.png|350px|center]] |
<h1>Modeling</h1> | <h1>Modeling</h1> | ||
| Line 63: | Line 63: | ||
<br>Methyl mercury transportation is mediated by the merE enzyme from the mer operon. The metal present in the environment of the cell is transported to the inner plant cell following the reaction: | <br>Methyl mercury transportation is mediated by the merE enzyme from the mer operon. The metal present in the environment of the cell is transported to the inner plant cell following the reaction: | ||
[[File:BIOSINTmodelEC.171.png|500px|center]] | [[File:BIOSINTmodelEC.171.png|500px|center]] | ||
| - | + | Where the metallic molecule is taken from the outside (MHgout) to the inside (MHgin) by a constant of reaction of KT and where K-T equals zero because the mercury inside cannot return to the exterior of the cell by the same reaction, given that mercury transportation mediated by merE is a one way process. | |
<br>Since the reaction is mediated by an enzyme, it could be expressed by: | <br>Since the reaction is mediated by an enzyme, it could be expressed by: | ||
[[File:BIOSINTmodelEC.17.png|550px|center]] | [[File:BIOSINTmodelEC.17.png|550px|center]] | ||
| - | + | Then, it is possible to model the process just as any other enzyme mediated reaction. For this purpose, we use the Michaelis-Menten equation. | |
[[File:BIOSINTmodelEC.18.png|500px|center]] | [[File:BIOSINTmodelEC.18.png|500px|center]] | ||
| - | + | Where v is the reaction rate, Vmax is the maximum rate achieved by the reaction at saturating substrate concentrations, S is the substrate and Km is the Michaelis constant for the reaction, or the substrate concentration when the system achieves half of Vmax. Therefore, adapting this for our process, we have: | |
[[File:BIOSINTmodelEC.19.png|500px|center]] | [[File:BIOSINTmodelEC.19.png|500px|center]] | ||
| Line 74: | Line 74: | ||
<br>Once in the interior of the cell, under slightly acid conditions, methyl mercury decays on methane and metallic mercury, by the following reaction: | <br>Once in the interior of the cell, under slightly acid conditions, methyl mercury decays on methane and metallic mercury, by the following reaction: | ||
[[File:BIOSINTmodelEC.20.png|550px|center]] | [[File:BIOSINTmodelEC.20.png|550px|center]] | ||
| - | + | Since the rate of the reaction in normal conditions is very low, we use merB to accelerate this rate. Therefore, the reaction can be described as: | |
[[File:BIOSINTmodelEC.21.png|550px|center]] | [[File:BIOSINTmodelEC.21.png|550px|center]] | ||
| - | + | Where methyl mercury is lysed by the merB protein at a rate that goes by the Michaelis-Menten equation: | |
[[File:BIOSINTmodelEC.22.png|500px|center]] | [[File:BIOSINTmodelEC.22.png|500px|center]] | ||
| - | + | Where the methyl mercury concentration is the concentration of the molecule inside the cell, described in the last step. | |
| Line 87: | Line 87: | ||
<br>From: | <br>From: | ||
[[File:BIOSINTmodelEC.23.png|550px|center]] | [[File:BIOSINTmodelEC.23.png|550px|center]] | ||
| - | + | Can be deduced for promoters with activators: | |
[[File:BIOSINTmodelEC.24.png|500px|center]] | [[File:BIOSINTmodelEC.24.png|500px|center]] | ||
| - | + | To find the complete demonstrations for the Hill’s equation for inducible promoters, you can visit Aberdeen 2009 wiki. | |
<br>Then, the activity for our promoter can be expressed as: | <br>Then, the activity for our promoter can be expressed as: | ||
[[File:BIOSINTmodelEC.25.png|500px|center]] | [[File:BIOSINTmodelEC.25.png|500px|center]] | ||
| - | + | Where βPCMV is the maximum expression achieved by our promoter. Kd is the constant is the equilibrium constant for the attachement of the inducer and the promoter, and n is the Hill’s coefficient for the cooperative ligation Induce-promoter. | |
<br> | <br> | ||
<br>Since the affinity of the tow molecules is high, the Hill’s coefficient is n>1, then, aPCMV, is also greater than one. Thus, the equations that models the expression of siRNAs are: | <br>Since the affinity of the tow molecules is high, the Hill’s coefficient is n>1, then, aPCMV, is also greater than one. Thus, the equations that models the expression of siRNAs are: | ||
| Line 98: | Line 98: | ||
[[File:BIOSINTmodelEC.27.png|550px|center]] | [[File:BIOSINTmodelEC.27.png|550px|center]] | ||
| - | + | And given that both sequences are connected to the same promoter, the activity is the same for siRBS1 and siIRES. | |
| Line 108: | Line 108: | ||
[[File:BIOSINTmodelEC.28.png|500px|center]] | [[File:BIOSINTmodelEC.28.png|500px|center]] | ||
| - | + | Where, merR is in charge of inhibiting the transcription rate. | |
<br>The negative feedback reaction can be expressed as: | <br>The negative feedback reaction can be expressed as: | ||
[[File:BIOSINTmodelEC.29.png|550px|center]] | [[File:BIOSINTmodelEC.29.png|550px|center]] | ||
| - | + | Being f (merR), the predictive function for the transcription rate. From the Hill’s function, it can be inferred for a repressed promoter that: | |
[[File:BIOSINTmodelEC.30.png|500px|center]] | [[File:BIOSINTmodelEC.30.png|500px|center]] | ||
| - | + | Then, the function for merR messenger is given by: | |
[[File:BIOSINTmodelEC.31.png|550px|center]] | [[File:BIOSINTmodelEC.31.png|550px|center]] | ||
| - | + | Thus, the function behavior will be cyclic, autoregulating itself. | |
| Line 125: | Line 125: | ||
[[File:BIOSINTmodelEC.32.png|500px|center]] | [[File:BIOSINTmodelEC.32.png|500px|center]] | ||
| - | + | Where DPC, represents the De-greening protein complex. Starting from this, we can infer the concentration of the construct by the equations: | |
[[File:BIOSINTmodelEC.33.png|550px|center]] | [[File:BIOSINTmodelEC.33.png|550px|center]] | ||
| - | + | Chalase: | |
[[File:BIOSINTmodelEC.34.png|500px|center]] | [[File:BIOSINTmodelEC.34.png|500px|center]] | ||
[[File:BIOSINTmodelEC.35.png|550px|center]] | [[File:BIOSINTmodelEC.35.png|550px|center]] | ||
| - | + | RCCR: | |
[[File:BIOSINTmodelEC.36.png|500px|center]] | [[File:BIOSINTmodelEC.36.png|500px|center]] | ||
[[File:BIOSINTmodelEC.37.png|550px|center]] | [[File:BIOSINTmodelEC.37.png|550px|center]] | ||
| - | + | PAO: | |
[[File:BIOSINTmodelEC.38.png|500px|center]] | [[File:BIOSINTmodelEC.38.png|500px|center]] | ||
[[File:BIOSINTmodelEC.39.png|550px|center]] | [[File:BIOSINTmodelEC.39.png|550px|center]] | ||
| - | + | And for GUN4: | |
[[File:BIOSINTmodelEC.40.png|550px|center]] | [[File:BIOSINTmodelEC.40.png|550px|center]] | ||
| + | |||
| + | <h2> References </h2> | ||
| + | |||
| + | Dekker, J., Vidal, M., & Walhout, A. M. (Eds.). (2014). Handbook of Systems Biology: Concepts and Insights. | ||
| + | |||
| + | Alon, U. (2006). An introduction to systems biology: design principles of biological circuits. CRC press. | ||
| + | |||
| + | Abramson, G. (2010). La matemática de los sistemas biológicos. | ||
| + | |||
| + | López, M. (1999). Un modelo matemático para el estudio de la incidencia del SIDA en la propagación de la tuberculosis (Doctoral dissertation, Tesis, Universidad Nacional de Colombia). | ||
| + | |||
| + | Klipp, E., Herwig, R., Kowald, A., Wierling, C., & Lehrach, H. (2008). Systems biology in practice: concepts, implementation and application. John Wiley & Sons. | ||
Latest revision as of 03:16, 18 October 2014
Modeling
This year we designed a construct where a lot of different genes interact in several ways. Eight sets of genes were constructed, using five distinctive kinds of genetic expression. They can be classified under the following categories:
a) Genes constitutively expressed
b) Genes that form a protein complex
c) Auto regulated networks
d) Simply induced sequences
e) Complex induced sequences
Equations for Phytochrome-PIF6 complex
In order to produce proteins, in the cell, two main reactions happen. First, DNA is transcripted to mRNA and then it is translated to a peptide sequence, it could be represented in the reaction by:
All these reactions are mediated by two specific enzymes, which are RNA polymerase (transcription) and ribosome (translation). These reactions have been well described in literature and can be modeled to a Ordinary Differential Equation system.
The rate of production of the PhyB construct is given by the rate of transcription of the protein from the mRNA molecule and the degradation of the messenger. Therefore:
Where γ is the translation rate of the cell, and α is the degradation of the degradation rate of the protein.
Also, the concentration of the messenger molecule is given by the equation
Where a represents the activity of the promoter, that is related to the capacity of being activated or suppressed by a transcription factor; β is the maximal production rate of the CaMV promoter (which is attached upstream to PhyB) and is a linear function dependent on the time of the reaction; as in the last equation, α is the degradation rate.
Also, since PCaMV is a constitutive promoter, the value of its activity is equal to 1. So the equation is reduced to
As PIF6 construct is connected to the same promoter, the equations of its expression are deduced by the same way, so:
In our system, both expressed gene constructs are part of another reaction in presence of deep red light (660 nm lightwave). When photoreceptor protein (PhyB construct) detects deep red light, it fuses to its interaction factor (PIF6 construct) and form a protein
For the complex creation, follow the following reaction in presence of 660 nm light.
Where Ku is the constant of the reaction, and is on concentration units. And K-u is the constant for the inverse reaction (separation of the complex), and the active form of the complex can be abbreviated as CPPA. Then, we can infer the concentration of active complex by the equation.
Also, in presence of far red light, the complex passes to its inactive form, represented as CPPI, by the following reaction:
Where KD is the constant of the reaction and K-D equals zero, because deactivated complex can’t return to its active form.
Then, if we despise the degradation rate of the inactivation of the protein complex, we can simplify the calculi of concentration of active photo protein by replacing 6 in 5.
Equations for mer Operon production
For the mer operon expression we start from the reaction
Of all the genes of this operon we used two specific proteins. merE is a transport protein in charge of the active transport od methyl-mercury from the environment of the cell to its interior. Once in the inner cytoplasm, merB protein attacks the molecule and breaks the covalent bond releasing methane and Hg2+(s) to the cell. Methane is metabolized and the quicksilver is accumulated.
Then, for the merE production rate we know that
And, as mer operon is attached to a minimal constitutive promoter (PCMV), the production rate of the messenger molecule is
The same process is applied to merB from the operon. Therefore:
Equations for Hg transportation
Methyl mercury transportation is mediated by the merE enzyme from the mer operon. The metal present in the environment of the cell is transported to the inner plant cell following the reaction:
Where the metallic molecule is taken from the outside (MHgout) to the inside (MHgin) by a constant of reaction of KT and where K-T equals zero because the mercury inside cannot return to the exterior of the cell by the same reaction, given that mercury transportation mediated by merE is a one way process.
Since the reaction is mediated by an enzyme, it could be expressed by:
Then, it is possible to model the process just as any other enzyme mediated reaction. For this purpose, we use the Michaelis-Menten equation.
Where v is the reaction rate, Vmax is the maximum rate achieved by the reaction at saturating substrate concentrations, S is the substrate and Km is the Michaelis constant for the reaction, or the substrate concentration when the system achieves half of Vmax. Therefore, adapting this for our process, we have:
Equations for mercury bioremediation
Once in the interior of the cell, under slightly acid conditions, methyl mercury decays on methane and metallic mercury, by the following reaction:
Since the rate of the reaction in normal conditions is very low, we use merB to accelerate this rate. Therefore, the reaction can be described as:
Where methyl mercury is lysed by the merB protein at a rate that goes by the Michaelis-Menten equation:
Where the methyl mercury concentration is the concentration of the molecule inside the cell, described in the last step.
Equations for the repressor system
The active protein complex that is formed by phyb construct and pif6 construct becomes a transcription factor that activates the production of two small interference RNAs. One is specific for the RBS1 sequence and the other for the IRES sequence.
Since the complex has a binding domain that joins to the promoter inducible PCMV, the rate of production of the siRNAs is given by the strength of the promoter and its activity (which is proportional to the activation by CPPA).
Since the activator has to bind to the DNA molecule in the promoter site, we use Hill’s function for macromolecules binding.
From:
Can be deduced for promoters with activators:
To find the complete demonstrations for the Hill’s equation for inducible promoters, you can visit Aberdeen 2009 wiki.
Then, the activity for our promoter can be expressed as:
Where βPCMV is the maximum expression achieved by our promoter. Kd is the constant is the equilibrium constant for the attachement of the inducer and the promoter, and n is the Hill’s coefficient for the cooperative ligation Induce-promoter.
Since the affinity of the tow molecules is high, the Hill’s coefficient is n>1, then, aPCMV, is also greater than one. Thus, the equations that models the expression of siRNAs are:
And given that both sequences are connected to the same promoter, the activity is the same for siRBS1 and siIRES.
Equations for de-greening regulatorsystem
An inducible two way promoter is connected downstream to a de-greening system and upstream to a regulator from the mer operon. This regulator, called merR, lead the expression of the PmerOT promoter.
In normal conditions, PmerOT promoter is induced by mercury in the cell and transcribes downstream. However, when HG is absent, PmerOT transcribes upstream and express the protein merR, which also works as an activator-repressor for PmerOT.
PmerOT repressed the expression upstream in a negative feedback. Reaction coul be expressed as:
Where, merR is in charge of inhibiting the transcription rate.
The negative feedback reaction can be expressed as:
Being f (merR), the predictive function for the transcription rate. From the Hill’s function, it can be inferred for a repressed promoter that:
Then, the function for merR messenger is given by:
Thus, the function behavior will be cyclic, autoregulating itself.
Equations for the downstream de-greening system
Downstream, PmerOT promoter will be activated by metallic mercury. Thus, the activity for the promoter downstream is given by the Hill’s function:
Where DPC, represents the De-greening protein complex. Starting from this, we can infer the concentration of the construct by the equations:
Chalase:
RCCR:
PAO:
And for GUN4:
References
Dekker, J., Vidal, M., & Walhout, A. M. (Eds.). (2014). Handbook of Systems Biology: Concepts and Insights.
Alon, U. (2006). An introduction to systems biology: design principles of biological circuits. CRC press.
Abramson, G. (2010). La matemática de los sistemas biológicos.
López, M. (1999). Un modelo matemático para el estudio de la incidencia del SIDA en la propagación de la tuberculosis (Doctoral dissertation, Tesis, Universidad Nacional de Colombia).
Klipp, E., Herwig, R., Kowald, A., Wierling, C., & Lehrach, H. (2008). Systems biology in practice: concepts, implementation and application. John Wiley & Sons.
 "
"