Team:Valencia UPV/Modeling/diffusion
From 2014.igem.org
Alejovigno (Talk | contribs) |
Alejovigno (Talk | contribs) |
||
| (48 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
<div align="center"><div id="cn-box" align="justify"> | <div align="center"><div id="cn-box" align="justify"> | ||
| - | <h3 class="hook" align="left"><a href=" | + | <h3 class="hook" align="left"><a href="#">Modeling</a> > <a href="https://2014.igem.org/Team:Valencia_UPV/Modeling/diffusion">Pheromone Diffusion</a></h3></p></br> |
<div align="center"><span class="coda"><roja>P</roja>heromone <roja>D</roja>iffusion <br/><br/> and <roja>M</roja>oths <roja>R</roja>esponse</span> </div> | <div align="center"><span class="coda"><roja>P</roja>heromone <roja>D</roja>iffusion <br/><br/> and <roja>M</roja>oths <roja>R</roja>esponse</span> </div> | ||
| Line 20: | Line 20: | ||
<div class="tab-content"> | <div class="tab-content"> | ||
<div id="tab1" class="tab active"> | <div id="tab1" class="tab active"> | ||
| - | <p> | + | <p>Sexual communication among moths is accomplished chemically by the release of an "odor" into the air. This "odor" consists of <span class="black-bold">sexual pheromones</span>.</p><br/> |
| - | < | + | <div align="center"><img width="540px" src="https://static.igem.org/mediawiki/2014/9/9d/VUPVIntro_sexpheromone.png" alt="female_sex_pheromones" title="Female and Male Moths"></img></div><br/> |
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.8em; width: 700px;"><span class="black-bold">Figure 1</span>. Female moth releasing sex pheromones and male moth.</p></div><br/> | ||
| - | |||
| - | |||
| - | <p>Using a modeling environment called <a class="normal-link-page" href=" | + | <p>Pheromones are molecules that easily diffuse in the air. During the diffusion process, the random movement of gas molecules transport the chemical away from its source [1]. Diffusion processes are complex ones, and modeling them analytically and with accuracy is difficult. Even more when the geometry is not simple. For this reason, we decided to consider a simplified model in which pheromone chemicals obey to the heat diffusion equation. Then, the equation is solved using the Euler numeric approximation in order to obtain the spatial and temporal distribution of pheromone concentration. </p><br/> |
| + | |||
| + | <p> Moths seem to respond to gradients of pheromone concentration to be attracted towards the source. Yet, there are other factors that lead moths to sexual pheromone sources, such as optomotor anemotaxis [2]. Moreover, increasing the pheromone concentration to unnaturally high levels may disrupt male orientation [3]. </p><br/> | ||
| + | |||
| + | <p>Using a modeling environment called <a class="normal-link-page" href="https://ccl.northwestern.edu/netlogo/">Netlogo</a>, we simulated the approximate moths behavior during the pheromone dispersion process. So, this will help us to predict moth response when they are also in presence of <span class="red-bold">Sexy Plant</span>.</p><br/> | ||
| + | |||
| + | <p align="left"><strong>References</strong></p><br/> | ||
| + | <div style="position: relative; left: 3%; width: 96%;"> | ||
| + | <ol> | ||
| + | <li> Sol I. Rubinow, Mathematical Problems in the Biological Sciences, chap. 9, SIAM, 1973</li> | ||
| + | <li> J. N. Perry and C. Wall , A Mathematical Model for the Flight of Pea Moth to Pheromone Traps Through a Crop, Phil. Trans. R. Soc. Lond. B 10 May 1984 vol. 306 no. 1125 19-48</li> | ||
| + | <li>W. L. Roelofs and R. T. Carde, Responses of Lepidoptera to synthetic sex pheromone chemicals and their analogues, Annual Review of Entomology | ||
| + | Vol. 22: 377-405, 1977</li> | ||
| + | </ol> | ||
| + | |||
</div> | </div> | ||
| + | </div> | ||
<div id="tab2" class="tab"> | <div id="tab2" class="tab"> | ||
<p>Since pheromones are chemicals released into the air, we have to consider both the motion of the fluid and the one of the particles suspended in the fluid.</p><br/> | <p>Since pheromones are chemicals released into the air, we have to consider both the motion of the fluid and the one of the particles suspended in the fluid.</p><br/> | ||
| - | <p>The motion of fluids can be described by the <span class="black-bold">Navier–Stokes equations</span>. But the | + | <p>The motion of fluids can be described by the <span class="black-bold">Navier–Stokes equations</span>. But the typical nonlinearity of these equations when there may exist turbulences in the air flow, makes most problems difficult or impossible to solve. Thus, attending to the particles suspended in the fluid, a simpler effective option for pheromone dispersion modeling consists in the assumption of pheromones diffusive-like behavior. |
| - | That is | + | That is, pheromones are molecules that can undergo a diffusion process in which the random movement of gas molecules transport the chemical away from its source [1].</p><br/> |
| - | <p>There are two ways to introduce the notion of diffusion: either a phenomenological approach starting with <span class="black-bold"> Fick's laws of diffusion</span> and their mathematical consequences, or a physical and atomistic one, by considering the <span class="black-bold"> random walk</span> of the diffusing particles.</p><br/> | + | <p>There are two ways to introduce the notion of diffusion: either using a phenomenological approach starting with <span class="black-bold"> Fick's laws of diffusion</span> and their mathematical consequences, or a physical and atomistic one, by considering the <span class="black-bold"> random walk</span> of the diffusing particles [2].</p><br/> |
| - | <p>In our case, we decided to | + | <p>In our case, we decided to model our diffusion process using the <span class="black-bold">Fick's laws</span>. Thus, it is postulated that the flux goes from regions of high concentration to regions of low concentration, with a magnitude that is proportional to the concentration gradient. However, diffusion processes are complex, and modelling them analytically and with accuracy is difficult. Even more when the geometry is not simple (e.g. consider the potential final distribution of our plants in the crop field). For this reason, we decided to consider a simplified model in which pheromone chemicals obey the heat diffusion equation.</p><br/><br/> |
| - | < | + | <p align="left"><strong>Approximation</strong></p><br/> |
</html> | </html> | ||
| - | The | + | The diffusion equation is a partial differential equation that describes density dynamics |
in a material undergoing diffusion. It is also used to describe processes exhibiting | in a material undergoing diffusion. It is also used to describe processes exhibiting | ||
| - | diffusive-like behavior, like in our case. | + | diffusive-like behavior, like in our case. The equation is usually written as: |
| - | + | ||
| - | The equation is usually written as: | + | |
| - | $$\frac{\partial \phi (r,t) }{\partial t} = \nabla | + | $$\frac{\partial \phi (r,t) }{\partial t} = \nabla • [D(\phi,r) \nabla \phi(r,t)]$$ |
| - | where $\phi(r, t)$ is the density of the diffusing material at location r and time t and | + | where $\phi(r, t)$ is the density of the diffusing material at location r and time t, and |
$D(\phi, r)$ is the collective diffusion coefficient for density $\phi$ at location $r$; and | $D(\phi, r)$ is the collective diffusion coefficient for density $\phi$ at location $r$; and | ||
$\nabla$ represents the vector differential operator. | $\nabla$ represents the vector differential operator. | ||
If the diffusion coefficient does not depend on the density then the equation is linear and | If the diffusion coefficient does not depend on the density then the equation is linear and | ||
| - | $D$ is constant. Thus, the equation reduces to the | + | $D$ is constant. Thus, the equation reduces to the linear differential equation: |
$$\frac{\partial \phi (r,t) }{\partial t} = D \nabla^2 \phi(r,t)$$ | $$\frac{\partial \phi (r,t) }{\partial t} = D \nabla^2 \phi(r,t)$$ | ||
| - | also called the '''heat equation'''. | + | also called the '''heat equation'''. Making use of this equation we can write the pheromones chemicals diffusion equation with no |
| - | + | ||
| - | Making use of this equation we can write pheromones chemicals diffusion equation with no | + | |
wind effect consideration as: | wind effect consideration as: | ||
| Line 70: | Line 80: | ||
where c is the pheromone concentration, $\Delta$ is the Laplacian operator, and $D$ is | where c is the pheromone concentration, $\Delta$ is the Laplacian operator, and $D$ is | ||
| - | the pheromone diffusion constant in air. | + | the pheromone diffusion constant in the air.<br/> |
| - | If we consider the wind, we face a diffusion system with drift and an advection term is | + | If we consider the wind, we face a diffusion system with drift, and an advection term is |
added to the equation above. | added to the equation above. | ||
$$\frac{\partial c }{\partial t} = D \nabla^2 c - \nabla \cdot (\vec{v} c )$$ | $$\frac{\partial c }{\partial t} = D \nabla^2 c - \nabla \cdot (\vec{v} c )$$ | ||
| - | where $\vec{v}$ is the average ''velocity'' | + | where $\vec{v}$ is the average ''velocity''. Thus, $\vec{v}$ |
| - | would be the velocity of the air flow.<br/> | + | would be the velocity of the air flow in or case.<br/> |
For simplicity, we are not going to consider the third dimension. In $2D$ the equation | For simplicity, we are not going to consider the third dimension. In $2D$ the equation | ||
| Line 85: | Line 95: | ||
$$\frac{\partial c }{\partial t} = D \left(\frac{\partial^2 c }{\partial^2 x} + \frac{\partial^2 c }{\partial^2 y}\right) – \left(v_{x} \cdot \frac{\partial c }{\partial x} + v_{y} \cdot \frac{\partial c }{\partial y} \right) = D \left( c_{xx} + c_{yy}\right) - \left(v_{x} \cdot c_{x} + v_{y} \cdot c_{y}\right) $$ | $$\frac{\partial c }{\partial t} = D \left(\frac{\partial^2 c }{\partial^2 x} + \frac{\partial^2 c }{\partial^2 y}\right) – \left(v_{x} \cdot \frac{\partial c }{\partial x} + v_{y} \cdot \frac{\partial c }{\partial y} \right) = D \left( c_{xx} + c_{yy}\right) - \left(v_{x} \cdot c_{x} + v_{y} \cdot c_{y}\right) $$ | ||
| + | |||
<html><br/> | <html><br/> | ||
| Line 90: | Line 101: | ||
</html> | </html> | ||
| - | + | In order to determine a numeric solution for this partial differential equation, the so-called finite difference methods are used. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
With finite difference methods, partial differential equations are replaced by | With finite difference methods, partial differential equations are replaced by | ||
| - | its approximations | + | its approximations as finite differences, resulting in a system of algebraic equations. This is solved at each node |
| - | + | ||
$(x_i,y_j,t_k)$. These discrete values describe the temporal and spatial | $(x_i,y_j,t_k)$. These discrete values describe the temporal and spatial | ||
| - | distribution of the | + | distribution of the particles diffusing.<br/> |
| - | Although implicit methods are unconditionally stable so time steps could be larger and | + | Although implicit methods are unconditionally stable, so time steps could be larger and |
make the calculus process faster, the tool we have used to solve our heat equation is the | make the calculus process faster, the tool we have used to solve our heat equation is the | ||
| - | Euler explicit method | + | Euler explicit method, for it is the simplest option to approximate spatial derivatives.<br/><br/> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | The equation gives the new value of the pheromone level in terms of initial values | + | The equation gives the new value of the pheromone level in a given node in terms of initial values at that |
| - | node and its immediate neighbors. Since all these values are known the process is called | + | node and its immediate neighbors. Since all these values are known, the process is called |
explicit. | explicit. | ||
$$c(t_{k+1}) = c(t_k) + dt \cdot c'(t_k),$$ | $$c(t_{k+1}) = c(t_k) + dt \cdot c'(t_k),$$ | ||
| - | Now applying this method for the first case (with no wind consideration) we followed the | + | Now, applying this method for the first case (with no wind consideration) we followed the |
| - | next steps | + | next steps: |
1. Split time $t$ into $n$ slices of equal length <i>dt</i>: | 1. Split time $t$ into $n$ slices of equal length <i>dt</i>: | ||
| Line 121: | Line 124: | ||
\end{array} \right. $$ | \end{array} \right. $$ | ||
| - | 2. Considering the backward difference for the Euler explicit method | + | 2. Considering the backward difference for the Euler explicit method, the |
| - | expression that | + | expression that gives the current pheromone level each time step is: |
$$c (x, y, t) \approx c (x, y, t - dt ) + dt \cdot c'(x, y, t)$$ | $$c (x, y, t) \approx c (x, y, t - dt ) + dt \cdot c'(x, y, t)$$ | ||
| - | 3. And now considering the spatial dimension, | + | 3. And now considering the spatial dimension, central differences is applied to the Laplace operator $\Delta$, and backward differences are applied to the vector differential operator $\nabla$ (in 2D and assuming equal steps in x and y directions): |
$$c (x, y, t) \approx c (x, y, t - dt ) + dt \left( D \cdot \nabla^2 c (x, y, t) - \nabla \vec{v} c (x, y, t) \right)$$ | $$c (x, y, t) \approx c (x, y, t - dt ) + dt \left( D \cdot \nabla^2 c (x, y, t) - \nabla \vec{v} c (x, y, t) \right)$$ | ||
| Line 133: | Line 136: | ||
| - | With respect to the boundary conditions, they are null since we are considering an | + | With respect to the boundary conditions, they are null since we are considering an open space. Attending to the implementation and simulation of this method, <i>dt</i> must be small enough to avoid instability. |
| - | + | ||
<html> | <html> | ||
| + | |||
| + | <p align="left"><strong>References</strong></p><br/> | ||
| + | <div style="position: relative; left: 3%; width: 96%;"> | ||
| + | <ol> | ||
| + | <li> Sol I. Rubinow, Mathematical Problems in the Biological Sciences, chap. 9, SIAM, 1973</li> | ||
| + | <li> J. Philibert. One and a half century of diffusion: Fick, Einstein, before and beyond. Diffusion Fundamentals, 2,1.1-1.10, 2005.</li> | ||
| + | |||
| + | </ol> | ||
| + | </div> | ||
| Line 145: | Line 156: | ||
<h3>The Idea</h3><br/> | <h3>The Idea</h3><br/> | ||
| - | <p>When one | + | <p>When one observes moths behavior, they apparently move with erratic flight paths. This is possibly to avoid predators. This random flight is modified by the presence of sex pheromones. Since these are pheromones released by females in order to attract an individual of the opposite sex, it makes sense that males respond to <span class="purple-bold">gradients of sex pheromone concentration</span>, being attracted towards the source. As soon as a flying male <span class="green-bold">randomly</span> enters into a conical pheromone-effective sphere of sex pheromone released by a virgin female, the male begins to seek the female following a zigzag way. The male approaches the female, and finally copulates with her [1].</p><br/><br/><br/> |
| - | <p | + | <p align="left"><strong>Approximation</strong></p><br/> |
| + | <img width="150px" style="float:left; margin-right: 15px; margin-bottom: 15px;" src="https://static.igem.org/mediawiki/2014/1/17/VUPVPolillita_con_vectores_v1.png" alt="moth_array"></img> | ||
| - | < | + | <p>In <span class="red-bold">Sexy Plant</span> we approximate the resulting moth movement as a vectorial combination of a <span class="purple-bold">gradient vector</span> and a <span class="green-bold">random vector</span>. The magnitude of the gradient vector depends on the change in the pheromone concentration level between points separated by a differential stretch in space. More precisely, the gradient points in the direction of the greatest rate of increase of the function, and its magnitude is the slope of the graph in that direction. The random vector is constrained in this ‘moth response’ model by a fixed angle upper bound, assuming that the turning movement is relatively continuous. For example, one can asume that the moth cannot turn 180 degrees from one time instant to the next.</p><br/> |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | < | + | <p>Our synthetic plants are supposed to release enough sexual pheromone so as to be able to <span class="red-bold">saturate moth perception</span>. In this sense the resulting moth vector movement will depend ultimately on the pheromone concentration levels in the field and the moth ability to follow better or worse the gradient of sex pheromone concentration.</p><br/> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | < | + | <p>The three clases of male moth behavior we consider for the characterization of males moth behavior are described in Table 1.</p><br/> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | </ | + | </html> |
| + | [[File:Table_behavior.png|600px|center|Male moths behaviour characterization.]] | ||
| + | <html> | ||
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.9em; width: 700px;"><span class="black-bold">Table 1</span>. Male moths behaviour characterization.</p></div> | ||
| + | <p>This ensemble of behaviors can be translated into a sum of vectors in which the random vector has constant module and changing direction within a range, whereas the module of the gradient vector is a function of the gradient in the field. | ||
| + | The question now is how do we include the saturation effect in the resulting moth shift vector. With this in mind, and focusing on the implementation process, our approach consists on the following:</p> | ||
| - | < | + | <p>To model chemoattraction, the gradient vector will be always have fixed unit magnitude, and its direction is that of the greatest rate of increase of the pheromone concentration. </p><br/> |
| - | + | <p>To model the random flight, instead of using a random direction vector with constant module, we consider a random turning angle starting from the gradient vector direction.</p><br/> | |
| - | <p> | + | |
| - | + | <p>Thus, how do we include the saturation effect in the resulting moth shift vector? This is key to achieve sexual confusion. Our answer: the behaviour dependence on the moth saturation level --in turn related to the pheromone concentration in the field-- will be included in the random turning angle. </p><br/> | |
| - | |||
| + | </html> | ||
| + | [[File:Moth_vector.png|600px|center|Approximation of the male moths behaviour.]] | ||
| + | <html> | ||
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.9em; width: 700px;"><span class="black-bold">Table 1</span>. Approximation of the male moths behaviour.</p></div> | ||
| + | <p>This random turning angle will not follow a uniform distribution, but a Poisson distribution in which the mean is zero (no angle detour from the gradient vector direction) and the standard-deviation will be inversely proportional to the intensity of the gradient of sex pheromone concentration in the field. This approach leads to ‘sexual confusion’ of the insect as the field homogeneity increases. This is because the direction of displacement of the moth will equal the gradient direction with certain probability which depends on how saturated it is.</p><br/> | ||
| + | <p align="left"><strong>References</strong></p><br/> | ||
| + | <div style="position: relative; left: 3%; width: 96%;"> | ||
| + | <ol> | ||
| + | <li> Yoshitoshi Hirooka and Masana Suwanai. Role of Insect Sex Pheromone in Mating Behavior I. Theoretical Consideration on Release and Diffusion of Sex Pheromone in the Air. J. Ethol, 4, 1986</li> | ||
| + | </ol> | ||
| + | </div> | ||
| + | </div> | ||
| + | <div id="tab4" class="tab"> | ||
| + | <br/> | ||
| + | <p>Using a modeling environment called Netlogo, we simulate the approximate moth population behavior when the pheromone diffusion process take place.</p><br/> | ||
| + | <p> The <a href="http://ccl.northwestern.edu/netlogo/">Netlogo</a> simulator can be found in its website at Northwestern University. To download the source file of our <span class="red-bold">Sexy plant</span> simulation in Netlogo click here: | ||
| + | <a href="https://2014.igem.org/Team:Valencia_UPV/Modeling/sexyplants.nlogo" download>sexyplants.nlogo</a></p><br/> | ||
| - | <p> | + | <p align="left"><strong>Setup</strong></p><br/> |
| - | < | + | <ul style="list-style: disc; position: relative; left: 4%; width: 96%;"> |
| + | <li>We consider three <span class="black-bold">agents</span>: <span class="marron-bold">male</span> and <span class="fucsia-bold">female</span> moths, and <span class="red-bold">sexy plants</span>.</li> | ||
| + | <li>We have two kinds of sexual pheromone emission sources: <span class="fucsia-bold">female</span> moths and <span class="red-bold">sexyplants</span>. </li> | ||
| + | <li>Our scenario is an open crop field where <span class="red-bold">sexy plants</span> are intercropped, and moths fly following different patterns depending on its sex.</li> | ||
| + | </ul> | ||
| + | <p><span class="fucsia-bold">Females</span>, apart from emitting sexual pheromones, move following erratic random flight paths. After mating, females do not emit pheromones for a period of 2 hours.</p> | ||
| - | <p> | + | <p><span class="marron-bold">Males</span> also move randomly while they are under its detection threshold. But when they detect a certain pheromone concentration, they start to follow the pheromone concentration gradients until its saturation threshold is reached. </p> |
| - | <p> | + | <p> <span class="red-bold">Sexy plants</span> act as continuously- emitting sources, and their activity is regulated by a <span class="black-bold">Switch</span>.</p><br/> |
| - | <p></p><br/> | + | <p> The pheromone diffusion process, it is simulated in Netlogo by implementing the Euler explicit method. </p><br/> |
| - | <p></p>< | + | </html> |
| + | [[File:Upv_simu1.png|600px|center|Figure 1. NETLOGO Simulation environment.]] | ||
| + | <html> | ||
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.9em; width: 700px;"><span class="black-bold">Figure 1</span>. NETLOGO Simulation environment.</p></div> | ||
| - | <p></p><br/> | + | <p align="left"><strong>Runs</strong></p><br/> |
| - | + | <p>When <span class="red-bold">sexy plants</span> are switched-off, <span class="marron-bold">males</span> move randomly until they detect pheromone traces from <span class="fucsia-bold">females</span>. In that case they follow them. </p> | |
| + | <p>When <span class="red-bold">sexy plants</span> are switched-on, the pheromone starts to diffuse from them, rising up the concentration levels in the field. At first, <span class="red-bold">sexy plants</span> have the effect of acting as pheromone traps on the <span class="marron-bold">male</span> moths.</p><br/> | ||
| - | <div | + | |
| - | + | ||
| + | </html> | ||
| + | [[File:VUPV_Polillas.png|600px|center|Figure 2. On the left: sexy plants are switched-off and a male moth follows the pheromone trace from a female. On the right: sexy plants are switched on and a male moth go towards the static source as it happens with synthetic pheromone traps.]] | ||
| + | <html> | ||
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.9em; width: 700px;"><span class="black-bold">Figure 2</span>.On the left: sexy plants are switched-off and a male moth follows the pheromone trace from a female. On the right: sexy plants are switched on and a male moth go towards the static source as it happens with synthetic pheromone traps.</p></div> | ||
| + | |||
| + | <p>As the concentration rises in the field, it becomes more homogeneous. Remember that the <span class="green-bold">random turning angle</span> of the insect follows a Poisson distribution, in which the standard-deviation is inversely proportional to the intensity of the <span class="purple-bold">gradient</span>. Thus, the probability of the insect to take a bigger detour from the faced gradient vector direction is higher. This means that it is less able to follow pheromone concentration gradients, so sexual confusion is induced.</p> | ||
| + | |||
| + | <br/><br/><br/> | ||
| + | <div align="center"> | ||
| + | <iframe width="600" height="350" | ||
| + | src="http://www.youtube.com/embed/URZgjbfEUwc"> | ||
| + | </iframe><br/><br/> | ||
| + | </div> | ||
| + | <br/><br/> | ||
| + | <div align="center"><p style="text-align: justify; font-style: italic; font-size: 0.9em; width: 700px;"><span class="black-bold">Figure 3</span>. NETLOGO Simulation of the field: sexyplants, female moths, pheromone diffusion and male moths.</p></div> | ||
| + | <br/> | ||
| + | <p align="left"><strong>Parameters</strong></p><br/> | ||
| + | |||
| + | <p>The parameters of this model are not as well-characterized as we expected at first. Finding the accurate values of these parameters is not a trivial task. In the literature it is difficult to find a number experimentally obtained. So we decided to take an inverse engineering approach. The parameters ranges we found in the literature are: </p> <br/> | ||
| + | |||
| + | |||
| + | <dl> | ||
| + | <dt>Diffusion coefficient</dt> | ||
| + | <dd>Range of physical search: 0.01-0.2 cm^2/s <br/> | ||
| + | References: [1], [2], [3], [5]</dd> | ||
| + | <dt>Release rate (female)</dt> | ||
| + | <dd>Range of physical search: 0.02-1 µg/h <br/> | ||
| + | References: [4], [5], [8]</dd> | ||
| + | <dt>Release rate (Sexy Plant)</dt> | ||
| + | <dd>The range of search that we have considered is a little wider than the one for the release rate of females. <br/> | ||
| + | References: Primary sexpheromone components are approximately defined as those emitted by the calling insect that are obligatory | ||
| + | for trap catch in the field at component emission rates similar to that used by the insect [4].</dd> | ||
| + | <dt>Detection threshold</dt> | ||
| + | <dd>Range of physical search: 1000 molecules/ cm3<br/> | ||
| + | References: [4], [5], [8]</dd><br/> | ||
| + | <dt>Saturation threshold </dt> | ||
| + | <dd> References: It generally has been found that pheromone dispensers releasing the chemicals above a certain emission rate will catch fewer males. The optimum release rate or dispenser load for trap catch varies greatly among species [4].<br/> | ||
| + | Range of physical search: 1-5[Mass]/[ Distance]^2</dd><br/> | ||
| + | <dt>Moth sensitivity</dt> | ||
| + | <dd>This is a parameter referred to the capability of the insect to detect changes in pheromone concentration in the patch it is located and the neighbor patch. When the field becomes more homogeneous, an insect with higher sensitivity will be more able to follow the gradients. | ||
| + | </dd> | ||
| + | <dt>Wind force</dt> | ||
| + | <dd>Range: 0 - 10 m/s <br/> | ||
| + | References: [7] </dd> | ||
| + | <dt>Population</dt> | ||
| + | <dd>The number of males and females can be selected by the observer.</dd> | ||
| + | </dl> | ||
| + | |||
| + | |||
| + | <br/> | ||
| + | <br/> | ||
| + | <p align="left"><strong>Patches</strong></p><br/> | ||
| + | <p>One can modify the number of patches that conform the field so as to analyze its own case. In our case we used a field of 50x50 patches. </p> | ||
| + | <br/> | ||
| + | |||
| + | |||
| + | |||
| + | <p align="left"><strong>References</strong></p><br/> | ||
| + | <div style="position: relative; left: 3%; width: 96%;"> | ||
| + | <ol> | ||
| + | <li>Wilson et al.1969, Hirooka and Suwanai, 1976.</li> | ||
| + | <li>Monchich abd Mauson, 1961, Lugs, 1968.</li> | ||
| + | <li>G. A. Lugg. Diffusion Coefficients of Some Organic and Other Vapors in Air.</li> | ||
| + | <li>W. L. Roelofs and R. T. Carde. Responses of Lepidoptera to Synthetic Sex Pheromone Chemicals and their Analogues, Page 386. </li> | ||
| + | <li>R.W. Mankiny, K.W. Vick, M.S. Mayer, J.A. Coeffelt and P.S. Callahan (1980) Models For Dispersal Of Vapors in Open and Confined Spaces: Applications to Sex Pheromone Trapping in a Warehouse, Page 932, 940.</li> | ||
| + | <li> Tal Hadad, Ally Harari, Alex Liberzon, Roi Gurka (2013) On the correlation of moth flight to characteristics of a turbulent plume. </li> | ||
| + | <li> Average Weather For Valencia, Manises, Costa del Azahar, Spain. </li> | ||
| + | <li>Yoshitoshi Hirooka and Masana Suwanai. Role of Insect Sex Pheromone in Mating Behavior I. | ||
| + | Theoretical Consideration on Release and Diffusion of Sex Pheromone in the Air. | ||
| + | J. Ethol, 4, 1986</li> | ||
| + | </ol> | ||
</div> | </div> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
<div id="tab5" class="tab"> | <div id="tab5" class="tab"> | ||
| + | <br/> | ||
| + | <p align="left"><strong>Scenarios</strong></p><br/> | ||
| + | <p> | ||
| + | The aim consists of reducing the possibility of meeting among moths of opposite sex. Thus, we will analyze the number of meetings in the three following cases: | ||
| + | </p> | ||
| - | + | <ol style="position: relative; left: 4%; width: 90%;"> | |
| - | + | <li>When sexy plants are switched-off and males only interact with females.</li> | |
| - | + | <li>When sexy plants are switched-on and have the effect of trapping males.</li> | |
| - | <ol style="position: relative; left: | + | <li>When sexy plants are switched-on and males get confused as the level of pheromone concentration is higher than their saturation threshold.</li> |
| - | <li>When | + | |
| - | <li>When | + | |
| - | <li>When | + | |
</ol> | </ol> | ||
<p> | <p> | ||
| - | It is also interesting to analyze a fourth case, what does it happen if females wouldn’t emit pheromones and males just move randomly through the field? | + | It is also interesting to analyze a fourth case, what does it happen if females wouldn’t emit pheromones and males just move randomly through the field? This gives an idea of the minimum number of male-female encounters that we should expect in a fully random scenario, with no pheromones at play.</p> |
| - | <ol start="4"> | + | <ol start="4" style="position: relative; left: 4%; width: 90%;"> |
<li>Males and females move randomly. How much would our results differ from the rest of cases? </li> | <li>Males and females move randomly. How much would our results differ from the rest of cases? </li> | ||
</ol> | </ol> | ||
<p> | <p> | ||
| - | + | If Sexy Plant works, the first scenario should give higher number of encounters than the second and third ones. | |
</p> | </p> | ||
| + | <br/> | ||
| + | <p align="left"><strong>Scenarios</strong></p><br/> | ||
| + | <br/> | ||
| + | |||
| + | <p> | ||
| + | With all values fixed excepting the number of males and females, we started the simulations. Each test was simulated more than once, in order to consider the stochastic nature of the process. Again, we considered different sub-scenarios for each one of the cases mentioned above. In particular, we considered the cases of having male and female subpopulations of equal size, or one larger than the other one. | ||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | <br/> | ||
| + | <p align="left"><strong>Experiment 1</strong></p><br/> | ||
| + | <br/> | ||
| + | <p> | ||
| + | What does it happen when the number of females is equal to the number of males? (F=M) | ||
| + | </p> | ||
| + | <br/> | ||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li>T_{0} : Start</li> | ||
| + | <li>T_{1000}: Switch-ON</li> | ||
| + | <li>T_{2000}: End</li> | ||
| + | </ul> | ||
| + | <br/> | ||
| + | <p> The results show that the number of encounters during the time sexy plants are switched-on is almost the same, but in most cases lower than when sexy plants are switched-off. | ||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla1.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li>The time at which the insects start to get confused and move randomly is shorter as the population increases. Even for high numbers, males get confused before sexy plants are switched-on. That is because there is such amount of females that they saturate the field. This rarely happens in nature, so when this occurs in our simulation we should think that we are out of real scenarios, and then we should modify the rest of parameter values. In these experiments we see that at a population equal to 12 we start be on this limit (insects gets confused when the sexy plants are going to be switched-on). </li> | ||
| + | <li>An aspect that should also be considered is the time of the insects getting confused among experiments, (when the number of females is the same). One could think that this “saturation” time would depend on the number of encounters before it happens. Since females wouldn’t be emitting pheromones after mating, males should get confused later if the previous number of meetings is larger. However, results are not decisive in this matter.</li> | ||
| + | |||
| + | </ul> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | |||
| + | <br/> | ||
| + | <p align="left"><strong>Experiment 2</strong></p><br/> | ||
| + | <br/> | ||
| + | <p> | ||
| + | What does it happen when the number of females is equal to the number of males? (F=M) | ||
| + | </p> | ||
| + | <br/> | ||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li>T_{0} : Start</li> | ||
| + | <li>T_{1000}: Switch-ON</li> | ||
| + | <li>T_{2000}: End</li> | ||
| + | </ul> | ||
| + | <br/> | ||
| + | <p> Based on the results of experiment 1, we fixed 10 as the top number of females for the next tests. The number of females is conserved in each test. | ||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla2.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li>It is observed that the number of encounters is higher if the number of males increases (this makes sense). </li> | ||
| + | <li>In all cases it can be deduced that while the number of males increase against the number of females, the time required for them to get confused is larger. This possibly has its origin in the number of encounters, which is higher according to the first point. When males mate females, they give up emitting pheromones during a certain period of time, so the contribution to the field saturation decreases.</li> | ||
| + | </ul> | ||
| + | <br/> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla3.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | |||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li> | ||
| + | In contrast with the Experiment 1, it is observed that while the number of males increases, the number of encounters is considerably higher when sexy plants are switched-off than when they are switched-on. This is seen with more clarity when the number of males is larger. We believe that with more experiments, this fact can be easily tested.</li> | ||
| + | </ul> | ||
| + | |||
| + | <br/><br/> | ||
| + | <p align="left"><strong>Comparing Experiments 1 and 2</strong></p><br/> | ||
| + | <br/> | ||
| + | <p> | ||
| + | Experiment 1: F=10 M=10 | ||
| + | </p> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla4.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | <p> | ||
| + | In this experiment we did not see the result we are looking for. We are interested in obtaining a high proportion in the third column when sexy plants are working. We see that the graphs counting the number of encounters (purple for the Switch-OFF, green for the Switch-ON) are very similar, so the effect is not achieved satisfactorily. | ||
| + | </p> | ||
| + | <br/> | ||
| + | </html> | ||
| + | [[File:VUPV_difu_orito1.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | |||
| + | <p> | ||
| + | Experiment 2: F=10 M=30 | ||
| + | </p> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla5.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | <p> | ||
| + | In this experiment we do see the result we are looking for. We are interested in obtaining a high proportion in the third column when sexy plants are working. We see that the graphs counting the number of encounters (purple for the Switch-OFF, green for the Switch-ON) differ visibly, so the effect is achieved. | ||
| + | </p> | ||
| + | <br/> | ||
| + | </html> | ||
| + | [[File:VUPV_difu_orito2.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | |||
| + | |||
| + | <br/> | ||
| + | <p align="left"><strong>Experiment 3</strong></p><br/> | ||
| + | <br/> | ||
| + | <p> | ||
| + | <b>Females don’t emit pheromones. Thus, males and females move randomly. How much would our results differ from the ones with females emitting?</b> | ||
| + | </p> | ||
| + | <br/> | ||
| + | <p> | ||
| + | <We decided to set out the end time according to the moment in which the pheromone level in the field is entirely over the male saturation threshold (in this case 8). We take as reference the top population female number: 10. For the rest of tests the pheromone concentration in the field will be lower.</p> | ||
| + | <br/> | ||
| + | |||
| + | <ul style="position: relative; left: 4%; width: 90%;"> | ||
| + | <li>T_{0} : Start</li> | ||
| + | <li>T_{1700}: End</li> | ||
| + | </ul> | ||
| + | <br/> | ||
| + | |||
| + | <p> | ||
| + | In almost every cases, the number of encounters is higher when females emit pheromones. It means that in our model, males can follow females being guided by pheromone concentration gradients. Moreover, it is seen in the interface during simulations. Results for “pheromone emission”. Showed below are an average of an amount of experiments. | ||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla6.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | |||
| + | <p> | ||
| + | Also see the contribution of the pheromone supply to the environment depending on the number of females (directly related) and the number of meetings (inversely related) | ||
| + | For population 1 to 1 and this time ending given, no more than 2 encounters have been observed. In contrast with the random movement, in which not encounters have been showed in the range of experiments we have checked. | ||
| + | |||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | </html> | ||
| + | [[File:VUPV_difu_tabla7.png|600px|center]] | ||
| + | <html> | ||
| + | <br/> | ||
| + | |||
| + | <br/> | ||
| + | <p align="left"><strong>Conclusions</strong></p><br/> | ||
| + | <br/> | ||
| + | |||
| + | <p> | ||
| + | We have used a methodology for the results comparison in which experiments have been repeated several times. The interpretation of the performances has based on the values obtained. Nevertheless an exhaustive replay of the same realizations would give us more accurate values. | ||
| + | </p><br/> | ||
| + | <p> | ||
| + | The experiments with the same number of males than females give results we haven’t expected. Maybe changing the model parameter values one would obtain a different kind of performance. | ||
| + | </p> | ||
| + | <br/><p> | ||
| + | Other aspect that we have taken into account is that some of the encounters during the time males are following pheromone traces from females may be also due to random coincidence. | ||
| + | </p> | ||
| + | <br/><p> | ||
| + | We have used a procedure useful to discard scenarios and contrast different realizations. With this, logic conclusions can be derived. Thus, they are a way of leading a potential user of this application to widen the search of parameters and improve our model. And that could be useful to know the limitations of our system and helpful to decide the final distribution of our synthetic plants in the field. | ||
| + | </p> | ||
| + | <br/> | ||
| + | |||
| + | |||
| + | <br/> | ||
| + | </div> | ||
| + | |||
</div> | </div> | ||
</div> | </div> | ||
| Line 276: | Line 539: | ||
</html> | </html> | ||
| + | |||
{{:Team:Valencia_UPV/footer_img}} | {{:Team:Valencia_UPV/footer_img}} | ||
Latest revision as of 03:59, 18 October 2014
Modeling > Pheromone Diffusion
and
Sexual communication among moths is accomplished chemically by the release of an "odor" into the air. This "odor" consists of sexual pheromones.

Figure 1. Female moth releasing sex pheromones and male moth.
Pheromones are molecules that easily diffuse in the air. During the diffusion process, the random movement of gas molecules transport the chemical away from its source [1]. Diffusion processes are complex ones, and modeling them analytically and with accuracy is difficult. Even more when the geometry is not simple. For this reason, we decided to consider a simplified model in which pheromone chemicals obey to the heat diffusion equation. Then, the equation is solved using the Euler numeric approximation in order to obtain the spatial and temporal distribution of pheromone concentration.
Moths seem to respond to gradients of pheromone concentration to be attracted towards the source. Yet, there are other factors that lead moths to sexual pheromone sources, such as optomotor anemotaxis [2]. Moreover, increasing the pheromone concentration to unnaturally high levels may disrupt male orientation [3].
Using a modeling environment called Netlogo, we simulated the approximate moths behavior during the pheromone dispersion process. So, this will help us to predict moth response when they are also in presence of Sexy Plant.
References
- Sol I. Rubinow, Mathematical Problems in the Biological Sciences, chap. 9, SIAM, 1973
- J. N. Perry and C. Wall , A Mathematical Model for the Flight of Pea Moth to Pheromone Traps Through a Crop, Phil. Trans. R. Soc. Lond. B 10 May 1984 vol. 306 no. 1125 19-48
- W. L. Roelofs and R. T. Carde, Responses of Lepidoptera to synthetic sex pheromone chemicals and their analogues, Annual Review of Entomology Vol. 22: 377-405, 1977
Since pheromones are chemicals released into the air, we have to consider both the motion of the fluid and the one of the particles suspended in the fluid.
The motion of fluids can be described by the Navier–Stokes equations. But the typical nonlinearity of these equations when there may exist turbulences in the air flow, makes most problems difficult or impossible to solve. Thus, attending to the particles suspended in the fluid, a simpler effective option for pheromone dispersion modeling consists in the assumption of pheromones diffusive-like behavior. That is, pheromones are molecules that can undergo a diffusion process in which the random movement of gas molecules transport the chemical away from its source [1].
There are two ways to introduce the notion of diffusion: either using a phenomenological approach starting with Fick's laws of diffusion and their mathematical consequences, or a physical and atomistic one, by considering the random walk of the diffusing particles [2].
In our case, we decided to model our diffusion process using the Fick's laws. Thus, it is postulated that the flux goes from regions of high concentration to regions of low concentration, with a magnitude that is proportional to the concentration gradient. However, diffusion processes are complex, and modelling them analytically and with accuracy is difficult. Even more when the geometry is not simple (e.g. consider the potential final distribution of our plants in the crop field). For this reason, we decided to consider a simplified model in which pheromone chemicals obey the heat diffusion equation.
Approximation
The diffusion equation is a partial differential equation that describes density dynamics in a material undergoing diffusion. It is also used to describe processes exhibiting diffusive-like behavior, like in our case. The equation is usually written as:
$$\frac{\partial \phi (r,t) }{\partial t} = \nabla • [D(\phi,r) \nabla \phi(r,t)]$$
where $\phi(r, t)$ is the density of the diffusing material at location r and time t, and $D(\phi, r)$ is the collective diffusion coefficient for density $\phi$ at location $r$; and $\nabla$ represents the vector differential operator.
If the diffusion coefficient does not depend on the density then the equation is linear and $D$ is constant. Thus, the equation reduces to the linear differential equation: $$\frac{\partial \phi (r,t) }{\partial t} = D \nabla^2 \phi(r,t)$$
also called the heat equation. Making use of this equation we can write the pheromones chemicals diffusion equation with no wind effect consideration as:
$$\frac{\partial c }{\partial t} = D \nabla^2 C = D \Delta c$$
where c is the pheromone concentration, $\Delta$ is the Laplacian operator, and $D$ is
the pheromone diffusion constant in the air.
If we consider the wind, we face a diffusion system with drift, and an advection term is added to the equation above.
$$\frac{\partial c }{\partial t} = D \nabla^2 c - \nabla \cdot (\vec{v} c )$$
where $\vec{v}$ is the average velocity. Thus, $\vec{v}$
would be the velocity of the air flow in or case.
For simplicity, we are not going to consider the third dimension. In $2D$ the equation would be:
$$\frac{\partial c }{\partial t} = D \left(\frac{\partial^2 c }{\partial^2 x} + \frac{\partial^2 c }{\partial^2 y}\right) – \left(v_{x} \cdot \frac{\partial c }{\partial x} + v_{y} \cdot \frac{\partial c }{\partial y} \right) = D \left( c_{xx} + c_{yy}\right) - \left(v_{x} \cdot c_{x} + v_{y} \cdot c_{y}\right) $$

In order to determine a numeric solution for this partial differential equation, the so-called finite difference methods are used.
With finite difference methods, partial differential equations are replaced by
its approximations as finite differences, resulting in a system of algebraic equations. This is solved at each node
$(x_i,y_j,t_k)$. These discrete values describe the temporal and spatial
distribution of the particles diffusing.
Although implicit methods are unconditionally stable, so time steps could be larger and
make the calculus process faster, the tool we have used to solve our heat equation is the
Euler explicit method, for it is the simplest option to approximate spatial derivatives.
The equation gives the new value of the pheromone level in a given node in terms of initial values at that node and its immediate neighbors. Since all these values are known, the process is called explicit.
$$c(t_{k+1}) = c(t_k) + dt \cdot c'(t_k),$$
Now, applying this method for the first case (with no wind consideration) we followed the next steps:
1. Split time $t$ into $n$ slices of equal length dt: $$ \left\{ \begin{array}{c} t_0 &=& 0 \\ t_k &=& k \cdot dt \\ t_n &=& t \end{array} \right. $$
2. Considering the backward difference for the Euler explicit method, the expression that gives the current pheromone level each time step is:
$$c (x, y, t) \approx c (x, y, t - dt ) + dt \cdot c'(x, y, t)$$
3. And now considering the spatial dimension, central differences is applied to the Laplace operator $\Delta$, and backward differences are applied to the vector differential operator $\nabla$ (in 2D and assuming equal steps in x and y directions):
$$c (x, y, t) \approx c (x, y, t - dt ) + dt \left( D \cdot \nabla^2 c (x, y, t) - \nabla \vec{v} c (x, y, t) \right)$$ $$ D \cdot \nabla^2 c (x, y, t) = D \left( c_{xx} + c_{yy}\right) = D \frac{c_{i,j-1} + c_{i,j+1} + c_{i-1,j } + c_{i+1,j} – 4 c_{I,j}}{s} $$ $$ \nabla \vec{v} c (x, y, t) = v_{x} \cdot c_{x} + v_{y} \cdot c_{y} = v_{x} \frac{c_{i,j} – c_{i-1,j}}{h} + v_{y} \frac{c_{i,j} – c_{i,j-1}}{h} $$
With respect to the boundary conditions, they are null since we are considering an open space. Attending to the implementation and simulation of this method, dt must be small enough to avoid instability.
References
- Sol I. Rubinow, Mathematical Problems in the Biological Sciences, chap. 9, SIAM, 1973
- J. Philibert. One and a half century of diffusion: Fick, Einstein, before and beyond. Diffusion Fundamentals, 2,1.1-1.10, 2005.
The Idea
When one observes moths behavior, they apparently move with erratic flight paths. This is possibly to avoid predators. This random flight is modified by the presence of sex pheromones. Since these are pheromones released by females in order to attract an individual of the opposite sex, it makes sense that males respond to gradients of sex pheromone concentration, being attracted towards the source. As soon as a flying male randomly enters into a conical pheromone-effective sphere of sex pheromone released by a virgin female, the male begins to seek the female following a zigzag way. The male approaches the female, and finally copulates with her [1].
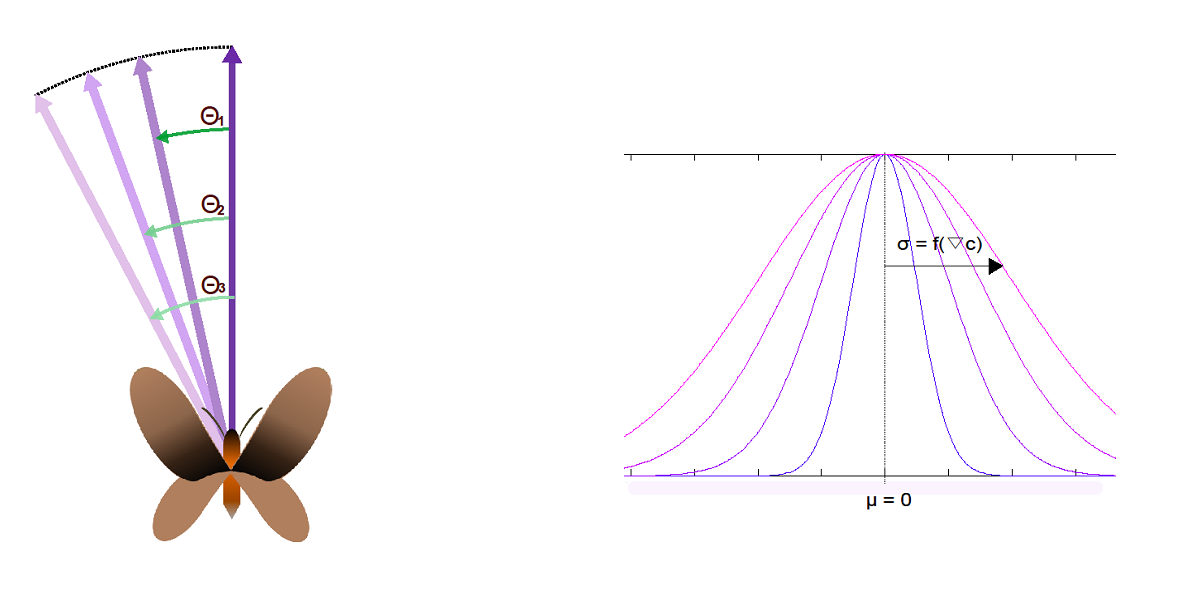
Approximation

In Sexy Plant we approximate the resulting moth movement as a vectorial combination of a gradient vector and a random vector. The magnitude of the gradient vector depends on the change in the pheromone concentration level between points separated by a differential stretch in space. More precisely, the gradient points in the direction of the greatest rate of increase of the function, and its magnitude is the slope of the graph in that direction. The random vector is constrained in this ‘moth response’ model by a fixed angle upper bound, assuming that the turning movement is relatively continuous. For example, one can asume that the moth cannot turn 180 degrees from one time instant to the next.
Our synthetic plants are supposed to release enough sexual pheromone so as to be able to saturate moth perception. In this sense the resulting moth vector movement will depend ultimately on the pheromone concentration levels in the field and the moth ability to follow better or worse the gradient of sex pheromone concentration.
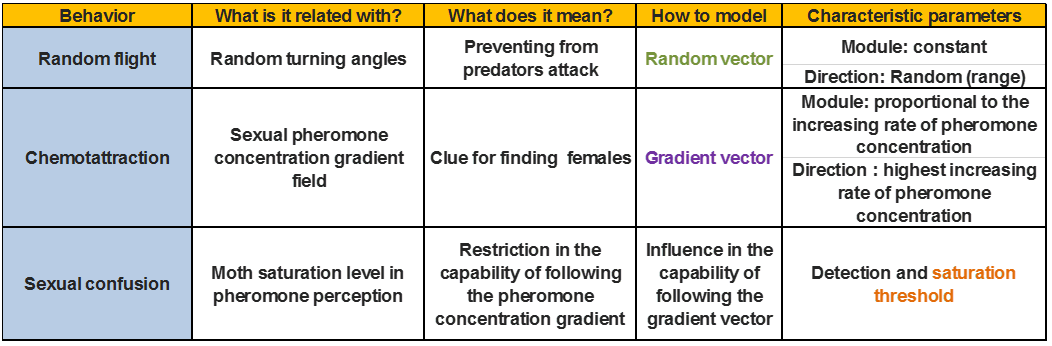
The three clases of male moth behavior we consider for the characterization of males moth behavior are described in Table 1.
Table 1. Male moths behaviour characterization.
This ensemble of behaviors can be translated into a sum of vectors in which the random vector has constant module and changing direction within a range, whereas the module of the gradient vector is a function of the gradient in the field. The question now is how do we include the saturation effect in the resulting moth shift vector. With this in mind, and focusing on the implementation process, our approach consists on the following:
To model chemoattraction, the gradient vector will be always have fixed unit magnitude, and its direction is that of the greatest rate of increase of the pheromone concentration.
To model the random flight, instead of using a random direction vector with constant module, we consider a random turning angle starting from the gradient vector direction.
Thus, how do we include the saturation effect in the resulting moth shift vector? This is key to achieve sexual confusion. Our answer: the behaviour dependence on the moth saturation level --in turn related to the pheromone concentration in the field-- will be included in the random turning angle.
Table 1. Approximation of the male moths behaviour.
This random turning angle will not follow a uniform distribution, but a Poisson distribution in which the mean is zero (no angle detour from the gradient vector direction) and the standard-deviation will be inversely proportional to the intensity of the gradient of sex pheromone concentration in the field. This approach leads to ‘sexual confusion’ of the insect as the field homogeneity increases. This is because the direction of displacement of the moth will equal the gradient direction with certain probability which depends on how saturated it is.
References
- Yoshitoshi Hirooka and Masana Suwanai. Role of Insect Sex Pheromone in Mating Behavior I. Theoretical Consideration on Release and Diffusion of Sex Pheromone in the Air. J. Ethol, 4, 1986
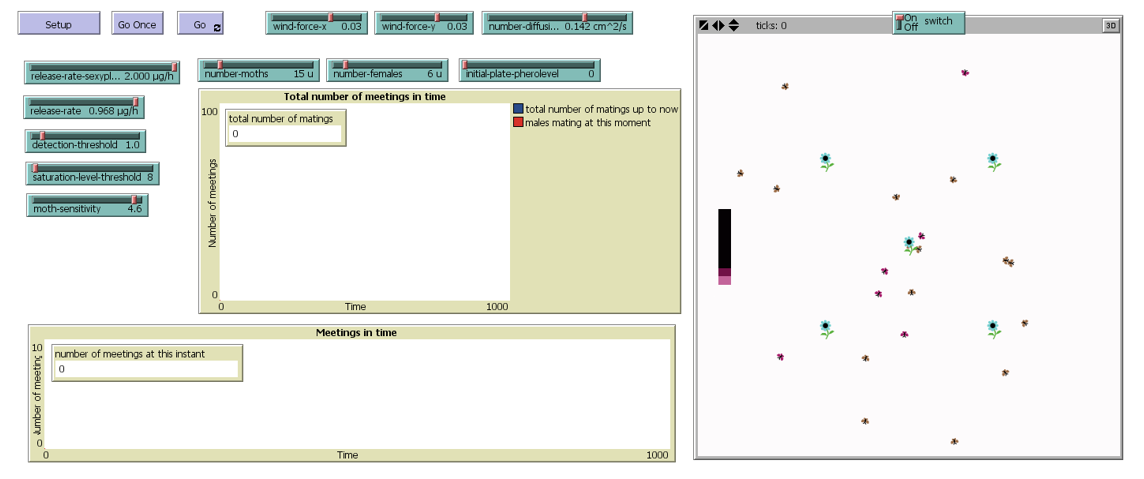
Using a modeling environment called Netlogo, we simulate the approximate moth population behavior when the pheromone diffusion process take place.
The Netlogo simulator can be found in its website at Northwestern University. To download the source file of our Sexy plant simulation in Netlogo click here: sexyplants.nlogo
Setup
- We consider three agents: male and female moths, and sexy plants.
- We have two kinds of sexual pheromone emission sources: female moths and sexyplants.
- Our scenario is an open crop field where sexy plants are intercropped, and moths fly following different patterns depending on its sex.
Females, apart from emitting sexual pheromones, move following erratic random flight paths. After mating, females do not emit pheromones for a period of 2 hours.
Males also move randomly while they are under its detection threshold. But when they detect a certain pheromone concentration, they start to follow the pheromone concentration gradients until its saturation threshold is reached.
Sexy plants act as continuously- emitting sources, and their activity is regulated by a Switch.
The pheromone diffusion process, it is simulated in Netlogo by implementing the Euler explicit method.
Figure 1. NETLOGO Simulation environment.
Runs
When sexy plants are switched-off, males move randomly until they detect pheromone traces from females. In that case they follow them.
When sexy plants are switched-on, the pheromone starts to diffuse from them, rising up the concentration levels in the field. At first, sexy plants have the effect of acting as pheromone traps on the male moths.
Figure 2.On the left: sexy plants are switched-off and a male moth follows the pheromone trace from a female. On the right: sexy plants are switched on and a male moth go towards the static source as it happens with synthetic pheromone traps.
As the concentration rises in the field, it becomes more homogeneous. Remember that the random turning angle of the insect follows a Poisson distribution, in which the standard-deviation is inversely proportional to the intensity of the gradient. Thus, the probability of the insect to take a bigger detour from the faced gradient vector direction is higher. This means that it is less able to follow pheromone concentration gradients, so sexual confusion is induced.
Figure 3. NETLOGO Simulation of the field: sexyplants, female moths, pheromone diffusion and male moths.
Parameters
The parameters of this model are not as well-characterized as we expected at first. Finding the accurate values of these parameters is not a trivial task. In the literature it is difficult to find a number experimentally obtained. So we decided to take an inverse engineering approach. The parameters ranges we found in the literature are:
- Diffusion coefficient
- Range of physical search: 0.01-0.2 cm^2/s
References: [1], [2], [3], [5] - Release rate (female)
- Range of physical search: 0.02-1 µg/h
References: [4], [5], [8] - Release rate (Sexy Plant)
- The range of search that we have considered is a little wider than the one for the release rate of females.
References: Primary sexpheromone components are approximately defined as those emitted by the calling insect that are obligatory for trap catch in the field at component emission rates similar to that used by the insect [4]. - Detection threshold
- Range of physical search: 1000 molecules/ cm3
References: [4], [5], [8] - Saturation threshold
- References: It generally has been found that pheromone dispensers releasing the chemicals above a certain emission rate will catch fewer males. The optimum release rate or dispenser load for trap catch varies greatly among species [4].
Range of physical search: 1-5[Mass]/[ Distance]^2 - Moth sensitivity
- This is a parameter referred to the capability of the insect to detect changes in pheromone concentration in the patch it is located and the neighbor patch. When the field becomes more homogeneous, an insect with higher sensitivity will be more able to follow the gradients.
- Wind force
- Range: 0 - 10 m/s
References: [7] - Population
- The number of males and females can be selected by the observer.
Patches
One can modify the number of patches that conform the field so as to analyze its own case. In our case we used a field of 50x50 patches.
References
- Wilson et al.1969, Hirooka and Suwanai, 1976.
- Monchich abd Mauson, 1961, Lugs, 1968.
- G. A. Lugg. Diffusion Coefficients of Some Organic and Other Vapors in Air.
- W. L. Roelofs and R. T. Carde. Responses of Lepidoptera to Synthetic Sex Pheromone Chemicals and their Analogues, Page 386.
- R.W. Mankiny, K.W. Vick, M.S. Mayer, J.A. Coeffelt and P.S. Callahan (1980) Models For Dispersal Of Vapors in Open and Confined Spaces: Applications to Sex Pheromone Trapping in a Warehouse, Page 932, 940.
- Tal Hadad, Ally Harari, Alex Liberzon, Roi Gurka (2013) On the correlation of moth flight to characteristics of a turbulent plume.
- Average Weather For Valencia, Manises, Costa del Azahar, Spain.
- Yoshitoshi Hirooka and Masana Suwanai. Role of Insect Sex Pheromone in Mating Behavior I. Theoretical Consideration on Release and Diffusion of Sex Pheromone in the Air. J. Ethol, 4, 1986
Scenarios
The aim consists of reducing the possibility of meeting among moths of opposite sex. Thus, we will analyze the number of meetings in the three following cases:
- When sexy plants are switched-off and males only interact with females.
- When sexy plants are switched-on and have the effect of trapping males.
- When sexy plants are switched-on and males get confused as the level of pheromone concentration is higher than their saturation threshold.
It is also interesting to analyze a fourth case, what does it happen if females wouldn’t emit pheromones and males just move randomly through the field? This gives an idea of the minimum number of male-female encounters that we should expect in a fully random scenario, with no pheromones at play.
- Males and females move randomly. How much would our results differ from the rest of cases?
If Sexy Plant works, the first scenario should give higher number of encounters than the second and third ones.
Scenarios
With all values fixed excepting the number of males and females, we started the simulations. Each test was simulated more than once, in order to consider the stochastic nature of the process. Again, we considered different sub-scenarios for each one of the cases mentioned above. In particular, we considered the cases of having male and female subpopulations of equal size, or one larger than the other one.
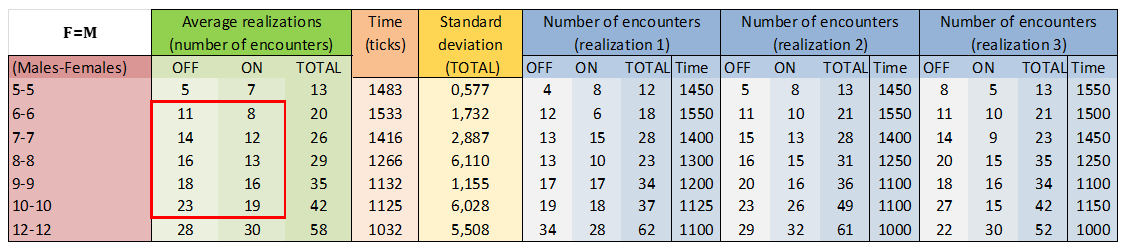
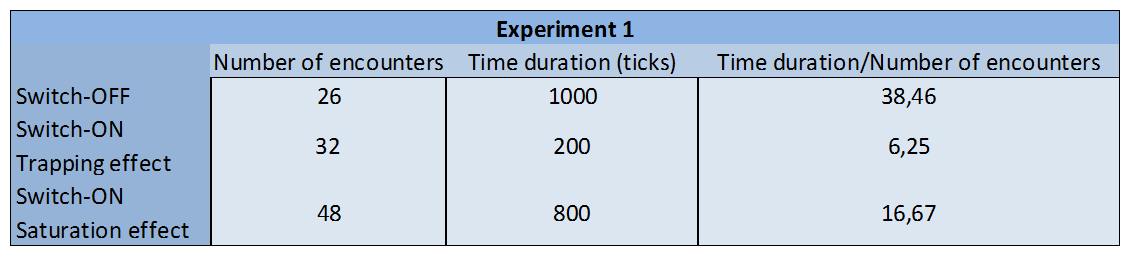
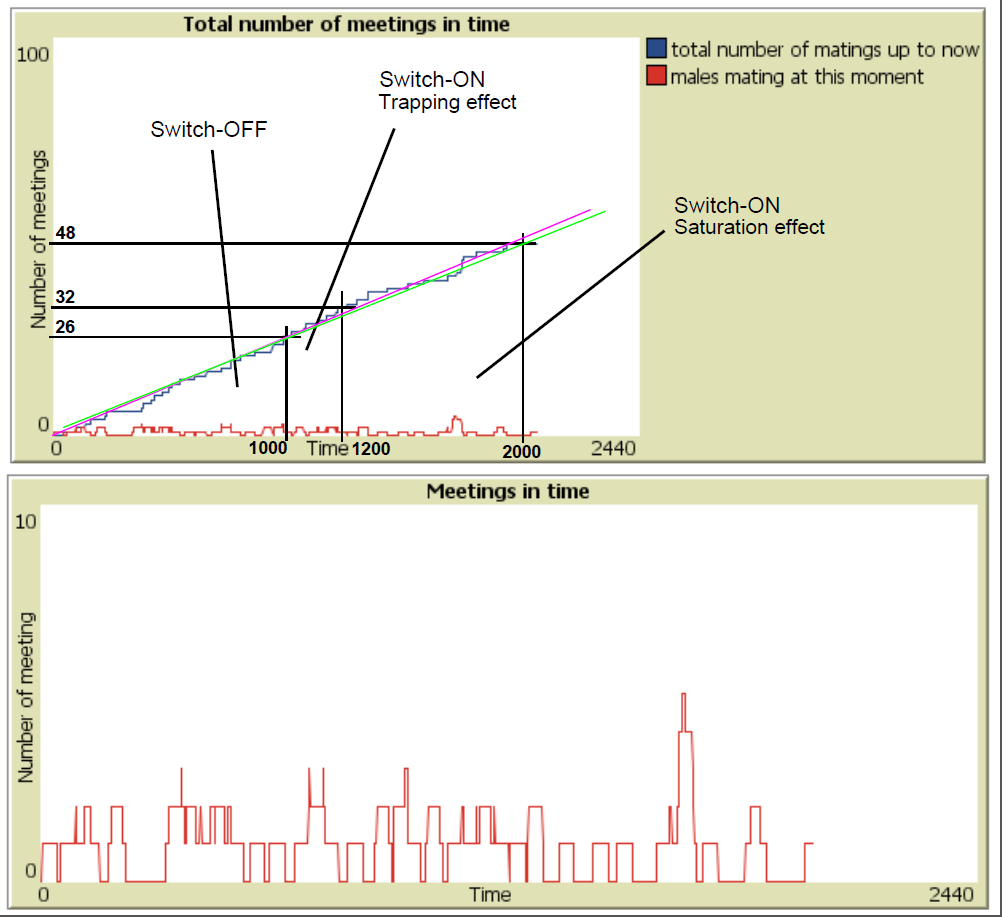
Experiment 1
What does it happen when the number of females is equal to the number of males? (F=M)
- T_{0} : Start
- T_{1000}: Switch-ON
- T_{2000}: End
The results show that the number of encounters during the time sexy plants are switched-on is almost the same, but in most cases lower than when sexy plants are switched-off.
- The time at which the insects start to get confused and move randomly is shorter as the population increases. Even for high numbers, males get confused before sexy plants are switched-on. That is because there is such amount of females that they saturate the field. This rarely happens in nature, so when this occurs in our simulation we should think that we are out of real scenarios, and then we should modify the rest of parameter values. In these experiments we see that at a population equal to 12 we start be on this limit (insects gets confused when the sexy plants are going to be switched-on).
- An aspect that should also be considered is the time of the insects getting confused among experiments, (when the number of females is the same). One could think that this “saturation” time would depend on the number of encounters before it happens. Since females wouldn’t be emitting pheromones after mating, males should get confused later if the previous number of meetings is larger. However, results are not decisive in this matter.
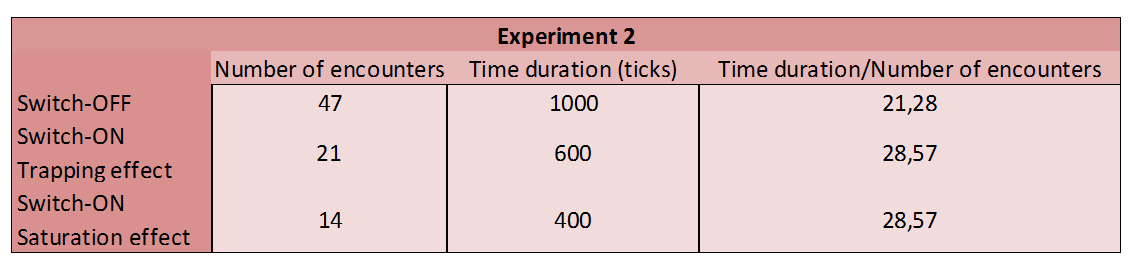
Experiment 2
What does it happen when the number of females is equal to the number of males? (F=M)
- T_{0} : Start
- T_{1000}: Switch-ON
- T_{2000}: End
Based on the results of experiment 1, we fixed 10 as the top number of females for the next tests. The number of females is conserved in each test.
- It is observed that the number of encounters is higher if the number of males increases (this makes sense).
- In all cases it can be deduced that while the number of males increase against the number of females, the time required for them to get confused is larger. This possibly has its origin in the number of encounters, which is higher according to the first point. When males mate females, they give up emitting pheromones during a certain period of time, so the contribution to the field saturation decreases.
- In contrast with the Experiment 1, it is observed that while the number of males increases, the number of encounters is considerably higher when sexy plants are switched-off than when they are switched-on. This is seen with more clarity when the number of males is larger. We believe that with more experiments, this fact can be easily tested.
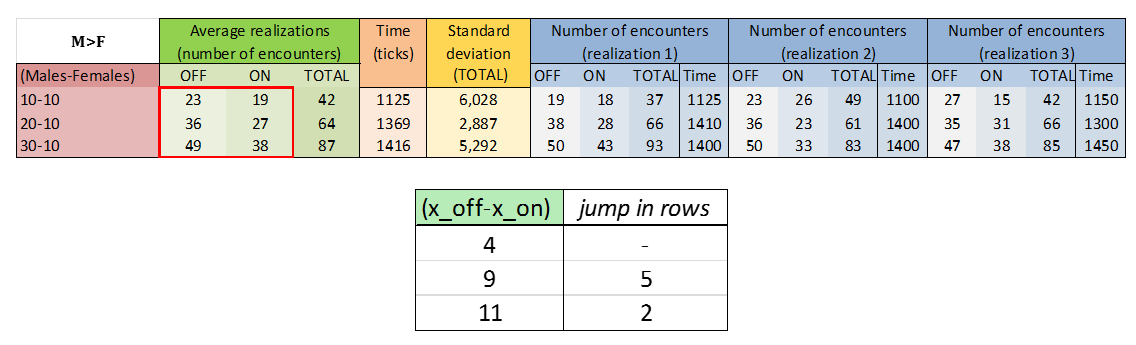
Comparing Experiments 1 and 2
Experiment 1: F=10 M=10
In this experiment we did not see the result we are looking for. We are interested in obtaining a high proportion in the third column when sexy plants are working. We see that the graphs counting the number of encounters (purple for the Switch-OFF, green for the Switch-ON) are very similar, so the effect is not achieved satisfactorily.
Experiment 2: F=10 M=30
In this experiment we do see the result we are looking for. We are interested in obtaining a high proportion in the third column when sexy plants are working. We see that the graphs counting the number of encounters (purple for the Switch-OFF, green for the Switch-ON) differ visibly, so the effect is achieved.
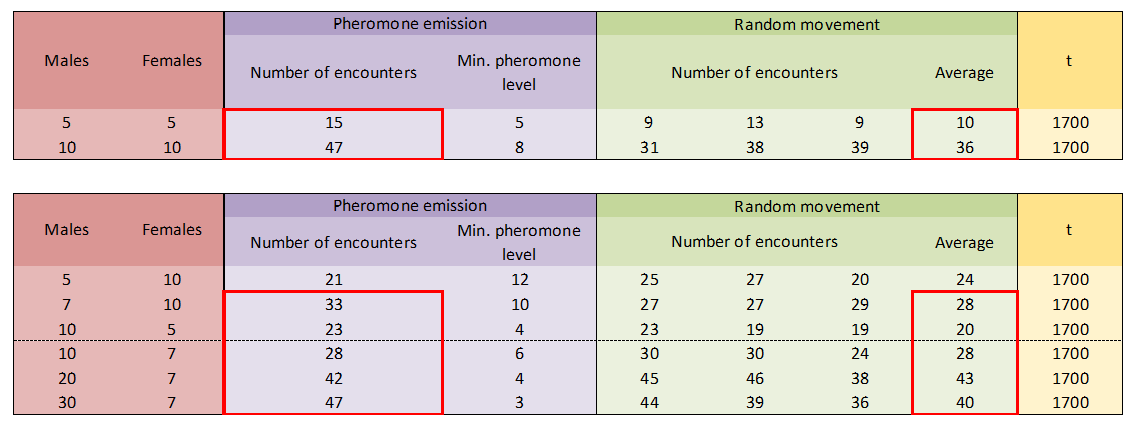
Experiment 3
Females don’t emit pheromones. Thus, males and females move randomly. How much would our results differ from the ones with females emitting?
In almost every cases, the number of encounters is higher when females emit pheromones. It means that in our model, males can follow females being guided by pheromone concentration gradients. Moreover, it is seen in the interface during simulations. Results for “pheromone emission”. Showed below are an average of an amount of experiments.
Also see the contribution of the pheromone supply to the environment depending on the number of females (directly related) and the number of meetings (inversely related) For population 1 to 1 and this time ending given, no more than 2 encounters have been observed. In contrast with the random movement, in which not encounters have been showed in the range of experiments we have checked.
Conclusions
We have used a methodology for the results comparison in which experiments have been repeated several times. The interpretation of the performances has based on the values obtained. Nevertheless an exhaustive replay of the same realizations would give us more accurate values.
The experiments with the same number of males than females give results we haven’t expected. Maybe changing the model parameter values one would obtain a different kind of performance.
Other aspect that we have taken into account is that some of the encounters during the time males are following pheromone traces from females may be also due to random coincidence.
We have used a procedure useful to discard scenarios and contrast different realizations. With this, logic conclusions can be derived. Thus, they are a way of leading a potential user of this application to widen the search of parameters and improve our model. And that could be useful to know the limitations of our system and helpful to decide the final distribution of our synthetic plants in the field.
Go to Modeling Overview Go to Pheromone Production
 "
"