Team:NCTU Formosa/modeling

From 2014.igem.org

(Difference between revisions)
(→MATLAB Introduction)
m (→Modeling Introduction)
 
(278 intermediate revisions not shown)
Line 1: Line 1:
{{:Team:NCTU Formosa/source/head}}
{{:Team:NCTU Formosa/source/head}}
{{:Team:NCTU Formosa/source/header-modeling}}
{{:Team:NCTU Formosa/source/header-modeling}}
-
{{:Team:NCTU Formosa/source/header}}
+
{{:Team:NCTU Formosa/source/header0}}
{{:Team:NCTU Formosa/source/cover-modeling}}
{{:Team:NCTU Formosa/source/cover-modeling}}
{{:Team:NCTU Formosa/source/card}}
{{:Team:NCTU Formosa/source/card}}
Line 7: Line 7:
<div class="li"><div class="card">
<div class="li"><div class="card">
-
===MATLAB Introduction===
+
===Modeling Introduction===
-
<p>MATLAB (matrix laboratory) is a numerical computing environment and fourth-generation programming language. It is developed by MathWorks, a company in United States. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, Java, and Fortran. Although MATLAB is intended primarily for numerical computing, '''an optional toolbox''' uses the MuPAD symbolic engine, allowing access to symbolic computing capabilities. An additional package, Simulink, adds '''graphical multi-domain simulation''' and''' Model-Based Design''' for dynamic and embedded systems.</p>
+
In the modeling part, we make two models in our project to optimize our result and enhance the convenience of the device usage. In the first model, we demonstrate a model for our biobricks which is composed of P<sub>cons</sub>, RBS, 9 PBAN, BFP, and Terminator. And in the second model, we model our device with two kinds of natural factor which are temperature and the wavelength of light.
-
<br>
+
<p>In this project, we use two main function of ANFIS, which is data adjusting and data simulating, in our PBAN model and device model. '''In PBAN model''', '''we use a theoretical biobrick to adjust our experiment data''', and '''in device model''', we use the simulation function to find a prediction surface to '''predict the insect capture performance of our device'''. These result will describe in the following parts.</p>
-
 
+
<p>The following contents we can divide into three parts:</p>  
-
[[File:https://2014.igem.org/File:MO_fig.1.png|160px|thumb|center|]]
+
<p>(1) Modeling of PBAN: First, we use ANFIS to build PBAN model that can fit to theoretical estimation and real condition at the 　　　　same time.</p>
 +
<p>(2) Modeling of Device: Second, a device model is also established. This model can let the user know the insect capture 　　　　performance in any condition.</p>
 +
<p>(3) Modeling Software: At last, we introduce the tool we use. ANFIS, a tool involved in MATLAB. </p>
</div></div>
</div></div>
<div class="li"><div class="card">
<div class="li"><div class="card">
-
===ANFIS Introduction===
+
===Modeling of PBAN===
-
<p>Adaptive-Network-Based Fuzzy Inference System, in short ANFIS, is a power tool for constructing a set of fuzzy if-then rules to generate stipulated output and input pairs. Unlike system modeling using mathematical rules that lacks the ability to deal with ill-defined and uncertain system, '''ANFIS can transform human knowledge into rule base, and therefore, ANFIS can effectively tune membership functions, minimizing the output error.'''</p>
+
In this project, 9 kinds of PBAN are used to attract 9 different kinds of insects into our device. Even though these 9 PBAN (PBAN(BM), PBAN(MB), PBAN(AI), PBAN(LD), PBAN(HAH), PBAN(AS), PBAN(SI), PBAN(AA), PBAN(SL)) facilitates the production of pheromone through different pathways, 9 PBAN are translated with the same promoter and RBS in ''E.coli'', and therefore, the production rate for each PBAN should be the same. With that said, we use a “P<sub>cons</sub> + RBS + BFP + Ter” as the theoretical condition to simulate PBAN biobrick (P<sub>cons</sub> + RBS + PBAN + BFP + Ter) expression. By''' detecting the expression value from the theoretical biobrick and modifying by our PBAN biobrick expression''', this modified model can not only '''fit a theoretical condition''' that prevents our model from operating bias, but also '''fit to a real condition'''. To make a brief introduction of our PBAN model, the following contents are divided into two parts: (1) Theoretical biobrick (2) 9 different kinds of PBAN biobrick and modeling result.
 +
=====Theoretical biobrick=====
 +
[[File:theoretical.jpg|600px|center|thumb|Fig.2-1-1 A biobrick used as a template to simulate the PBAN biobrick expression.]]
 +
[[File:2014NCTU Formosa modeling Fig theoretical.png|600px|center|thumb|Fig.2-1-2 Theoretical biobrick expression profile.]]
 +
 +
=====9 different kinds of PBAN biobrick and modeling result=====
 +
1. P<sub>cons</sub> + RBS + PBAN(BM) + BFP + Ter [[File:ALLBM.png|780px|thumb||frameless|center|Fig.2-2-1 Biobrick of P<sub>cons</sub> + RBS + PBAN(BM) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN BM.png|780px|thumb||frameless|center|Fig.2-2-2 Modeling result of P<sub>cons</sub> + RBS + PBAN(BM) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(BM) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
2. P<sub>cons</sub> + RBS + PBAN(MB) + BFP + Ter [[File:ALLMB.png|780px|thumb||frameless|center|Fig.2-2-3 Biobrick of P<sub>cons</sub> + RBS + PBAN(MB) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN MB.png|780px|thumb||frameless|center|Fig.2-2-3 Modeling result of P<sub>cons</sub> + RBS + PBAN(MB) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(MB) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
3. P<sub>cons</sub> + RBS + PBAN(SL) + BFP + Ter [[File:ALLSL.png|780px|thumb||frameless|center|Fig.2-2-6 Biobrick of P<sub>cons</sub> + RBS + PBAN(SL) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN SL.png|780px||thumb|frameless|center|Fig.2-2-7 Modeling result of P<sub>cons</sub> + RBS + PBAN(SL) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(SL) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
4. P<sub>cons</sub> + RBS + PBAN(AI) + BFP + Ter [[File:ALLAI.png|780px|thumb||frameless|center|Fig.2-2-8 Biobrick of P<sub>cons</sub> + RBS + PBAN(AI) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN AI.png|780px|thumb||frameless|center|Fig.2-2-9 Modeling result of P<sub>cons</sub> + RBS + PBAN(AI) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(AI) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
5. P<sub>cons</sub> + RBS + PBAN(LD) + BFP + Ter [[File:ALLLD.png|780px|thumb||frameless|center|Fig.2-2-10 Biobrick of P<sub>cons</sub> + RBS + PBAN(LD) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN LD.png|780px|thumb||frameless|center|Fig.2-2-11 Modeling result of P<sub>cons</sub> + RBS + PBAN(LD) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(LD) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
6. P<sub>cons</sub> + RBS + PBAN(HAH) + BFP + Ter [[File:ALLHAH.png|780px|thumb||frameless|center|Fig.2-2-12 Biobrick of P<sub>cons</sub> + RBS + PBAN + PBAN(HAH) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN HAH.png|780px|thumb||frameless|center|Fig.2-2-13 Modeling result of P<sub>cons</sub> + RBS + PBAN(HAH) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(HAH) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
 +
7. P<sub>cons</sub> + RBS + PBAN(AS) + BFP + Ter [[File:ALLAS.png|780px|thumb||frameless|center|Fig.2-2-14 Biobrick of P<sub>cons</sub> + RBS + PBAN(AS) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN AS.png|780px|thumb||frameless|center|Fig.2-2-15 Modeling result of P<sub>cons</sub> + RBS + PBAN(AS) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(AS) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
 +
8. P<sub>cons</sub> + RBS + PBAN(SI) + BFP + Ter [[File:ALLSI.png|780px|thumb||frameless|center|Fig.2-2-16 Biobrick of P<sub>cons</sub> + RBS + PBAN(SI) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN SI.png|780px|thumb||frameless|center|Fig.2-2-17 Modeling result of P<sub>cons</sub> + RBS + PBAN(SI) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(SI) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
 +
 +
 +
 +
 +
9. P<sub>cons</sub> + RBS + PBAN + PBAN(AA) + BFP + Ter [[File:ALLAA.png|780px|thumb||frameless|center|Fig.2-2-18 Biobrick of P<sub>cons</sub> + RBS + PBAN + PBAN(AA) + BFP + Ter.]]
 +
[[File:2014NCTU Formosa modeling Fig PBAN AA.png|780px|thumb||frameless|center|Fig.3-10-2 Modeling result of P<sub>cons</sub> + RBS + PBAN(AA) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of P<sub>cons</sub> + RBS + PBAN(AA) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.]]
</div></div>
</div></div>
-
<div class="li"><div class="card">
 
-
===Single Unit===
 
-
====Red Promoter====
 
-
As shown in Figure 2,  the red promoter is consisted of P<sub>ompc</sub> and P<sub>lac</sub>. By multiplying the experimental data of P<sub>ompc</sub> + RBS + mGFP and P<sub>lac</sub> + RBS + mGFP, we would be able to build a model for the red promoter. This model, however, wouldn't be so accurate. To solve this problem, '''we used this model to train the actual experimental data of the red promoter by using ANFIS.''' Figure 2 is the result of such a training. We obtained '''a curve between our model and the actual experimental data.''' This curve is the representation of the new model that has been trained and supported by the actually experimental data of P<sub>red</sub>. This new model definitely contains a high degree of accuracy.
 
-
[[File:NCTU_Pred-value.jpg|center|Figure 2. using ANFIS to modified the simulated data by experimental data to obtain a more accurate result.]]
 
-
====Lux Promoter====
+
<div class="li"><div class="card">
-
<p>We did the following modeling based on the data obtained from Imperial 2007 iGEM team.
+
-
The data notes the strength of P<sub>lux</sub> under '''different concentrations of AHL''' and '''different time frames'''.</p>
+
-
[[File:Plux_testbiobrick.jpg|400px|center|Figure 3. the biobrick to test expression of the lux promoter]]
+
-
<p>
+
-
Using ANFIS to train 76 sets of data and to test 20 sets of data, we ontained Figure 4. It shows that '''our training data exhibits a similar trend as the testing data''', even though '''the computer has no based knowledge of the trend'''. This simply means that our modeling has successfully simulated the actually data. </p>
+
-
[[File:Nctu_Plux_train_wikifig.jpg|745px|center|Figure 4. The training and testing data using ANFIS system]]
+
-
Figure 5 is the resultant graph from input 1 (time) and input 2 (AHL concentration). According to this graph, we can observe the output (fluorescence) has two peaks about AHL concentration(at concentration of 4 nM and 40 nM).
+
-
That means '''we could achieve our regulation goal with little AHL.''' Also, pleas note that there is more output as time passes.
+
-
[[file:Nctu_Plux_ahl_time_wikifig.jpg|500px|center|Figure 5. Input 1 is time (min), input 2 is AHL concentration, and output is fluorescence.]]
+
-
====37 °C RBS====
+
===Modeling of Device===
-
<p>We used Figure 6 biobrick to model our 37<sup>o</sup>C RBS's function at different
+
The model we built should be able to predict the performance of our device under different conditions in which the device might be held function. This way, a user would be able to know what to expect from the device before using it. And the parameters chosen are  <br> (1) Wave Length (2) Temperature (3) Experiment Data
-
temperatures.</p>
+
-
[[File:Nctu_37rbs_biobricktest.jpg|400px|center|Figure 6. The biobrick used to test the temperature-regulated RBS function ]]
+
-
<p>
+
-
First, we did a experiment that test the fluroscence at different temperature and different time.
+
-
Choosing 100 sets of data to do machine learning, then we tested 20 sets of data. '''As Figure 7 shown, the curve can classify 4 groups fit in 27<sup>o</sup>C,32<sup>o</sup>C,37<sup>o</sup>C and 42<sup>o</sup>C.'''
+
-
</p>
+
-
[[File:Nctu_37_random_test.jpg|745px|center|Figure 7.The figure shows 100 training data composed by 4 different temperture (blue dot), and simulated result (red star).]]
+
-
<p>To test the accuracy of our model, we randomly chose 20 pairs of data which is not include in our training data to do the independent test, and the test result is shown in Figure 8. The blue dot in the figure represents the real experimental data that we randomly choose from our whole dataset, and the red star represents simulated result of our model. '''It is obviously showed that our model can accurately predict the biobrick function in any condition by using ANFIS.'''</p>
+
-
[[File:37rbs_test.png|745px|center|Figure 8. The blue dots represents the real experimental data. The red star represents simulated result of our model.]]
+
-
[[File:37rbs_model.jpg|center|500px|Figure 9. Input 1= Time (hr), Input 2= Temperature (degree Celsius), Output = Normalized expression (AU).]]
+
 +
=====Wave Length=====
 +
According to the reference, insects have '''chemotactic properties of light''', and different degrees of light will have different attractive effect, so we use  different kinds of wave lengths for testing to find the  best wave length for attracting moth.
 +
Variable Light－we divide the wave length of visible light into five parts－475, 510, 570 and 650 nm, and hope to end up with a model that simulate the effects of all wave lengths of light.
 +
[[File:2014NCTU Formosa_modeling_1.jpg|667px|center|thumb|Fig3-1-1 Visible light spectrum.]]
-
<p>From Figure 9, the maximum output is obtained at 37 <sup>o</sup>C. Under the same time frame, the output (the normalized expression of the reporter gene) is maximized at 37 <sup>o</sup>C while minimized at 25 <sup>o</sup>C. There is a dramatic decrease in the output below 30 <sup>o</sup>C and the outputs around 37<sup>o</sup>C are much higher. '''This modeling demonstrates that using 37 <sup>o</sup>C RBS is a plausible approach for achieving gene expression through temperature.''' </p>
+
=====Temperature=====
 +
Temperature is key factor that can significantly influence the performance of our device, and it is hard to change the surrounding temperature if you place the device in the field. We need to take temperature into consideration. We, therefore, selected five temperatures between the highest and lowest average temperature last year (17.03 ℃ / 30.1 ℃) of Taipei for modeling.
 +
[[File:2014NCTU Formosa modeling Fig average temperature.png|800px|center|thumb|Fig.3-2-1 Average temperature in Taiwan<sup>(1)</sup>.]]
 +
=====Experiment Data=====
 +
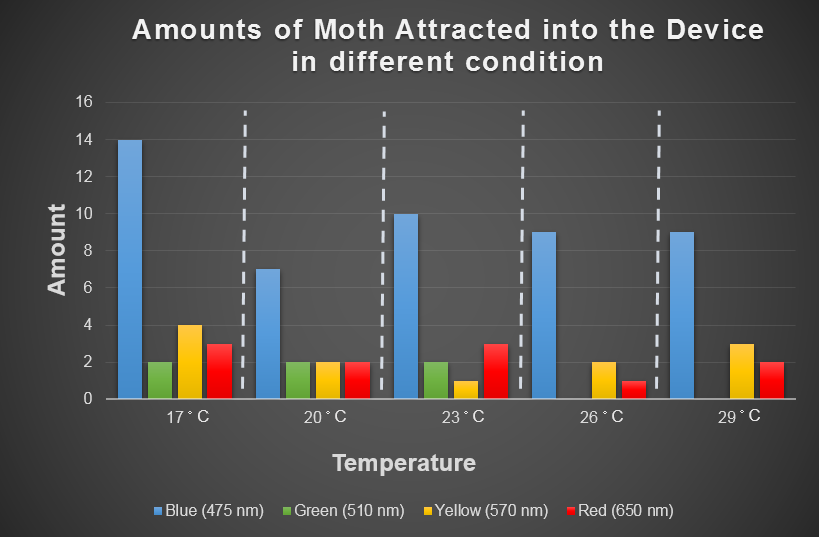
In the experiment part, we use CCW no.1 that we introduce in "Result/Insect Aspects" to evaluate the attracting ability of our device by changing the light wavelength and surrounding temperature. The '''insect would gather around a bottle based on their favor light color under consist temperature'''. This experiment is then repeated by changing the temperature from 17 to 29 degree Celsius. And the following table is our result.
 +
[[File:2014NCTU Formosa modeling Fig result.png|800px|center|thumb|Fig.3-3-1 The amount of moth attracted into oue device. Based on the result table, we can roughly find that blue light and 17 degree Celsius has the highest ability to attract insect. And the overall attraction ability is shown in our modeling result in Fig.3-3-3.]]
 +
[[File:Moth's_Behavior,_Temperature_and_Light.png|800px|center|thumb|Fig.3-3-2 The result of our model in bar chart.  ]]
 +
After experiment, the modeling using these data can simulate the capture ability in all conditions.
 +
[[File:2014NCTU Formosa modeling 6.png|800px|center|thumb|Fig.3-3-3 Simulating surface. The surface is composed of two conditional factor: surrounding temperature and light wavelength. And the surface can show the attraction ability in every temperature and light wavelength. This surface also means that user can know the attraction ability in any given condition which can significantly enhance the convenience of device usage. ]]
 +
The model of device aims to let the user easily input the condition value and know the device performance by this simulating surface. And the user can also find the local optima between the light wavelength 475 nm to 650 nm and the temperature between 17 to 29 degree Celsius.
======Reference======
======Reference======
<div class="rev">
<div class="rev">
<ol start="1">
<ol start="1">
-
<li>iGEM 2007 Imperial  https://2007.igem.org/Imperial</li>
+
<li>Central Weather Bureau of Taiwan http://stat.motc.gov.tw/mocdb/stmain.jsp?sys=100&funid=b8101</li>
</ol>
</ol>
</div>
</div>
</div></div>
</div></div>
 +
<div class="li"><div class="card">
<div class="li"><div class="card">
-
===E.colightuner Simulation===
+
===Modeling Software===
-
<p>We have all the modeling of each single unit . Now, we want to combine each unit to make a stimulation to the E.colightuner. </p>
+
=====MATLAB=====
-
[[File:Figure1_NCTU_Formosa.png|300px|center|Figure 10.The overall constituent of E.colightuner ]]
+
MATLAB (matrix laboratory) is a numerical computing environment and fourth-generation programming language. It is developed by MathWorks, a company in United States. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, Java, and Fortran. Although MATLAB is intended primarily for numerical computing, '''an optional toolbox''' uses the MuPAD symbolic engine, allowing access to symbolic computing capabilities. An additional package, Simulink, adds '''graphical multi-domain simulation''' and '''Model-Based Design''' for dynamic and embedded systems.
-
<p>Figure 10 shows the essential constituent of our E. colightuner. To save our efforts experimenting with this essential engine of E. colightuner, we built '''a model beforehand to help us evaluate its practicability.''' Our model is consisted of four components A, B, C, and D</p>
+
<br>[[File:matlab7.png|1000px|thumb|center|thumb|Fig.4-1-1 MATLAB icon.]]
-
[[File:Figure2_NCTU_Formosa.png|300px|center|Figure 11. component A ]]
+
 
-
<p>Figure 11 is the overall picture of our component A. Notice that component A is built from similar biobricks as our E.colightuner. The only difference between the two is the promoters used. '''Both P<sub>red</sub> of E.colightuner are substituted with P<sub>cons</sub> in component A.''' With that said, by taking the difference in the strength between P<sub>red</sub> and P<sub>cons</sub>, into calculations, we would be able to model out E. colightuner with component A. Before that, however, we would have to first build a model for component A. </p>
+
=====ANFIS=====
-
[[File:Figure3_NCTU_Formosa.png|300px|center|Figure 12. component B ]]
+
Adaptive-Network-Based Fuzzy Inference System, in short ANFIS, is a power tool for constructing a set of fuzzy if-then rules to generate stipulated output and input pairs. Unlike system modeling using mathematical rules that lacks the ability to deal with ill-defined and uncertain system, ANFIS can transform human knowledge into rule base, and therefore, '''ANFIS can effectively tune membership functions, minimizing the output error.'''
-
<P>To build a model for component A, we combined component B and C. As you can see in component B shown in Figure 12, it does not include P<sub>lux</sub> and luxR like component A. By assuming that when luxR is expressed, P<sub>lux</sub> would immediately reach its full strength, however, we can consider luxR and P<sub>lux</sub> pair as simply a Pcons,that is constitutively activated. From this perspective, component A and B are the same, except that component A is also effected by the translation efficiency of 37<sup>o</sup>C RBS. Component C is the model for 37<sup>o</sup>C RBS which was shown in the Single Unit part above. So '''by multiplying component C and component B, we would be able to obtain a model for component A.'''</p>
+
-
<p>In order to increase the accuracy of our component A model,''' we used ANFIS to fit our modeling result with the actual experimental data of our component A.''' By doing this, we obtained a new modeling curve for component that is more precise and accurate, shown in Figure 13. </p>
+
-
[[File:NCTU_A-value.jpg|center|Figure 13. using ANFIS to modified the simulated data by experimental data to obtain a more accurate result .]]
+
-
<p>As mentioned above, we needed to take the effect of P<sub>red</sub> into account before we could a model of E.colightuner based on component A. Component D has the model of P<sub>red</sub> built in a similar way as component A model which was shown before, too. We first built a model for P<sub>red</sub> and fitted it into the actual experimental data. </p>
+
-
<p>Having both precise model for component A and component D, we simply had to multiple them to obtain the final model for our E.Colightuner in Figure 14. </p>
+
-
[[File:Figure7_NCTU_Formosa.png|300px|center|Figure 14. the final model for E.colightuner . A = Figure2. B = Figure3. C = 37 degree celsius RBS , D = red promoter]]
+
-
Using the single unit to predict the project we simplify like Figure 10, we got Figure 15. The predictive curve is under red light and at 37<sup>o</sup>C. Due to the sRNA repression, the expression rate of mGFP is really low. This phenomenon is reasonable and interpretable. Thus, '''this modeling method can accurately predict the expression trend of a new biobrick.''' Applying this modeling system maturely, we can use computers to control our E.colightuner in the future.
 
-
[[File:Nctu_model_whole_project.jpg|800px|center|Figure 15. The Figure 14 predicted tendency.]]
 
</div></div>
</div></div>
-
 
-
 
-
{{:Team:NCTU Formosa/source/card-end}}
 
-
<html>
 
-
    <p>Cover image credit: <a href="http://www.dvq.co.nz/" target="_blank">DVQ</a></p>
 
-
    </div> </div>
 

Latest revision as of 03:21, 18 October 2014

Modeling

Change the font size right here

Contents

Modeling Introduction

In the modeling part, we make two models in our project to optimize our result and enhance the convenience of the device usage. In the first model, we demonstrate a model for our biobricks which is composed of Pcons, RBS, 9 PBAN, BFP, and Terminator. And in the second model, we model our device with two kinds of natural factor which are temperature and the wavelength of light.

In this project, we use two main function of ANFIS, which is data adjusting and data simulating, in our PBAN model and device model. In PBAN model, we use a theoretical biobrick to adjust our experiment data, and in device model, we use the simulation function to find a prediction surface to predict the insect capture performance of our device. These result will describe in the following parts.

The following contents we can divide into three parts:

(1) Modeling of PBAN: First, we use ANFIS to build PBAN model that can fit to theoretical estimation and real condition at the 　　　　same time.

(2) Modeling of Device: Second, a device model is also established. This model can let the user know the insect capture 　　　　performance in any condition.

(3) Modeling Software: At last, we introduce the tool we use. ANFIS, a tool involved in MATLAB.

Modeling of PBAN

In this project, 9 kinds of PBAN are used to attract 9 different kinds of insects into our device. Even though these 9 PBAN (PBAN(BM), PBAN(MB), PBAN(AI), PBAN(LD), PBAN(HAH), PBAN(AS), PBAN(SI), PBAN(AA), PBAN(SL)) facilitates the production of pheromone through different pathways, 9 PBAN are translated with the same promoter and RBS in E.coli, and therefore, the production rate for each PBAN should be the same. With that said, we use a “Pcons + RBS + BFP + Ter” as the theoretical condition to simulate PBAN biobrick (Pcons + RBS + PBAN + BFP + Ter) expression. By detecting the expression value from the theoretical biobrick and modifying by our PBAN biobrick expression, this modified model can not only fit a theoretical condition that prevents our model from operating bias, but also fit to a real condition. To make a brief introduction of our PBAN model, the following contents are divided into two parts: (1) Theoretical biobrick (2) 9 different kinds of PBAN biobrick and modeling result.

Theoretical biobrick
Fig.2-1-1 A biobrick used as a template to simulate the PBAN biobrick expression.
Fig.2-1-2 Theoretical biobrick expression profile.
9 different kinds of PBAN biobrick and modeling result
1. Pcons + RBS + PBAN(BM) + BFP + Ter
Fig.2-2-1 Biobrick of Pcons + RBS + PBAN(BM) + BFP + Ter.
Fig.2-2-2 Modeling result of Pcons + RBS + PBAN(BM) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(BM) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


2. Pcons + RBS + PBAN(MB) + BFP + Ter
Fig.2-2-3 Biobrick of Pcons + RBS + PBAN(MB) + BFP + Ter.
Fig.2-2-3 Modeling result of Pcons + RBS + PBAN(MB) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(MB) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


3. Pcons + RBS + PBAN(SL) + BFP + Ter
Fig.2-2-6 Biobrick of Pcons + RBS + PBAN(SL) + BFP + Ter.
Fig.2-2-7 Modeling result of Pcons + RBS + PBAN(SL) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(SL) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


4. Pcons + RBS + PBAN(AI) + BFP + Ter
Fig.2-2-8 Biobrick of Pcons + RBS + PBAN(AI) + BFP + Ter.
Fig.2-2-9 Modeling result of Pcons + RBS + PBAN(AI) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(AI) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


5. Pcons + RBS + PBAN(LD) + BFP + Ter
Fig.2-2-10 Biobrick of Pcons + RBS + PBAN(LD) + BFP + Ter.
Fig.2-2-11 Modeling result of Pcons + RBS + PBAN(LD) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(LD) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


6. Pcons + RBS + PBAN(HAH) + BFP + Ter
Fig.2-2-12 Biobrick of Pcons + RBS + PBAN + PBAN(HAH) + BFP + Ter.
Fig.2-2-13 Modeling result of Pcons + RBS + PBAN(HAH) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(HAH) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.



7. Pcons + RBS + PBAN(AS) + BFP + Ter
Fig.2-2-14 Biobrick of Pcons + RBS + PBAN(AS) + BFP + Ter.
Fig.2-2-15 Modeling result of Pcons + RBS + PBAN(AS) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(AS) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.



8. Pcons + RBS + PBAN(SI) + BFP + Ter
Fig.2-2-16 Biobrick of Pcons + RBS + PBAN(SI) + BFP + Ter.
Fig.2-2-17 Modeling result of Pcons + RBS + PBAN(SI) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(SI) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.



9. Pcons + RBS + PBAN + PBAN(AA) + BFP + Ter
Fig.2-2-18 Biobrick of Pcons + RBS + PBAN + PBAN(AA) + BFP + Ter.
Fig.3-10-2 Modeling result of Pcons + RBS + PBAN(AA) + BFP + Ter. The blue line is the expression profile of the theoretical biobrick. And the green line is the expression data of Pcons + RBS + PBAN(AA) + BFP + Ter. And the red line is the adjusting line from the green and blue one. This line represent the correcting line of theoretical data and real condition data which can make our model not only fit the theoretical condition but also stay away from experimental bias.


Modeling of Device

The model we built should be able to predict the performance of our device under different conditions in which the device might be held function. This way, a user would be able to know what to expect from the device before using it. And the parameters chosen are
(1) Wave Length (2) Temperature (3) Experiment Data

Wave Length

According to the reference, insects have chemotactic properties of light, and different degrees of light will have different attractive effect, so we use different kinds of wave lengths for testing to find the best wave length for attracting moth. Variable Light－we divide the wave length of visible light into five parts－475, 510, 570 and 650 nm, and hope to end up with a model that simulate the effects of all wave lengths of light.

Fig3-1-1 Visible light spectrum.
Temperature

Temperature is key factor that can significantly influence the performance of our device, and it is hard to change the surrounding temperature if you place the device in the field. We need to take temperature into consideration. We, therefore, selected five temperatures between the highest and lowest average temperature last year (17.03 ℃ / 30.1 ℃) of Taipei for modeling.

Fig.3-2-1 Average temperature in Taiwan(1).
Experiment Data

In the experiment part, we use CCW no.1 that we introduce in "Result/Insect Aspects" to evaluate the attracting ability of our device by changing the light wavelength and surrounding temperature. The insect would gather around a bottle based on their favor light color under consist temperature. This experiment is then repeated by changing the temperature from 17 to 29 degree Celsius. And the following table is our result.

Fig.3-3-1 The amount of moth attracted into oue device. Based on the result table, we can roughly find that blue light and 17 degree Celsius has the highest ability to attract insect. And the overall attraction ability is shown in our modeling result in Fig.3-3-3.
Fig.3-3-2 The result of our model in bar chart.

After experiment, the modeling using these data can simulate the capture ability in all conditions.

Fig.3-3-3 Simulating surface. The surface is composed of two conditional factor: surrounding temperature and light wavelength. And the surface can show the attraction ability in every temperature and light wavelength. This surface also means that user can know the attraction ability in any given condition which can significantly enhance the convenience of device usage.

The model of device aims to let the user easily input the condition value and know the device performance by this simulating surface. And the user can also find the local optima between the light wavelength 475 nm to 650 nm and the temperature between 17 to 29 degree Celsius.

Reference
  1. Central Weather Bureau of Taiwan http://stat.motc.gov.tw/mocdb/stmain.jsp?sys=100&funid=b8101

Modeling Software

MATLAB

MATLAB (matrix laboratory) is a numerical computing environment and fourth-generation programming language. It is developed by MathWorks, a company in United States. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, Java, and Fortran. Although MATLAB is intended primarily for numerical computing, an optional toolbox uses the MuPAD symbolic engine, allowing access to symbolic computing capabilities. An additional package, Simulink, adds graphical multi-domain simulation and Model-Based Design for dynamic and embedded systems.


Fig.4-1-1 MATLAB icon.
ANFIS

Adaptive-Network-Based Fuzzy Inference System, in short ANFIS, is a power tool for constructing a set of fuzzy if-then rules to generate stipulated output and input pairs. Unlike system modeling using mathematical rules that lacks the ability to deal with ill-defined and uncertain system, ANFIS can transform human knowledge into rule base, and therefore, ANFIS can effectively tune membership functions, minimizing the output error.


Retrieved from "http://2014.igem.org/Team:NCTU_Formosa/modeling"