Team:Oxford/progress
From 2014.igem.org
MatthewBooth (Talk | contribs) |
|||
| Line 7: | Line 7: | ||
<div class="container cf row"> | <div class="container cf row"> | ||
<h1>Modelling Progress</h1> | <h1>Modelling Progress</h1> | ||
| + | |||
| + | <h2>Week 5 Day 2 </h2> | ||
| + | <div class="news_block"> | ||
| + | <h2>Leroy says:</h2> | ||
| + | <p>This was my first day back after taking about a week off for family reasons. Matt has continued the stochastic modelling which I started off on Friday of Week 3. I spent today developing the diffusive aspect of the stochastic modelling and have successfully modeled the diffusive motion, according to the Smoluchowski equations, of DCM and DCMA within the microcompartment. The model is such that DCMA molecules cannot diffuse through the microcompartment but DCM molecules can move in and out unhindered due to their small size. </p> | ||
| + | </div> | ||
| + | |||
<h2>Week 5 Day 1 </h2> | <h2>Week 5 Day 1 </h2> | ||
Revision as of 13:12, 12 August 2014
Modelling Progress
Week 5 Day 2
Leroy says:
This was my first day back after taking about a week off for family reasons. Matt has continued the stochastic modelling which I started off on Friday of Week 3. I spent today developing the diffusive aspect of the stochastic modelling and have successfully modeled the diffusive motion, according to the Smoluchowski equations, of DCM and DCMA within the microcompartment. The model is such that DCMA molecules cannot diffuse through the microcompartment but DCM molecules can move in and out unhindered due to their small size.
Week 5 Day 1
Matt says:
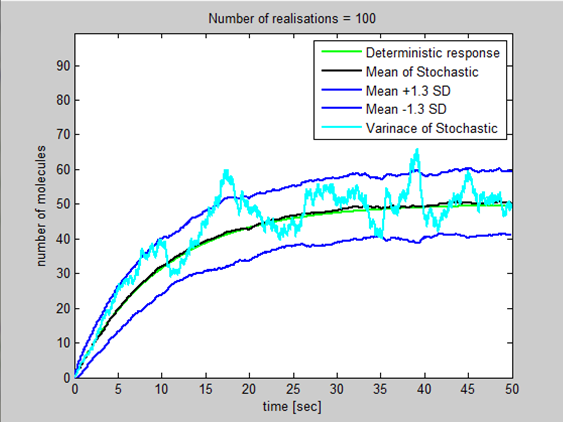
I went through the derivation of a general stochastic model today and proved that the steady state variance=steady state mean=k2/k1 where k2=production constant and k1=degradation constant. I introduced this variance into ProductionDegradation3 then using Standard deviation=(Variance)^0.5 introduced a basic upper/lower bound for the population by adding and taking away 1.3 standard deviation to the mean. This gives us a confidence interval of 90% that the population will lie between the 2 blue lines. (Assuming the variation in population around the mean can be modelled using the normal distribution)
Week 4 Day 5
Oliver says:
Spent the morning checking over my repressor/activator network responses in preparation to present the data to the biochemistry department. Then had the weekly department meeting. In the afternoon we sorted out access to most areas of the Engineering department, then Skyped with the Univesity of Sheffield about potential collaboration ideas. There is quite a lot of cross over in the human practices area and it was also suggested that we may be able to stochastically model their constitutively expressing bacteria. Finally, edited Matlab graphs for the presentation.
Matt says:
Finally managed to get the mean working for the Gillepsie Algorithm, though I'm not sure if my version ended up being any less data heavy than the modified version (ProductionDegradation3). I will look at some of Oliver's other models and see if they can be simulated as well. Might be doing fluorescent cell microscopy in the afternoon with Lucas and Oliver.
Week 4 Day 4
Matt says:
Stochastic modelling looks like deterministic model as more and more realisations are added. Made a bit of progress on getting the mean of the Gillepsie Algorithm, but it is a lot harder than originally thought
Oliver says:
Building the presentation to give to the department about iGEM.
Week 4 Day 3
Matt says:
In the morning I simulated another of the examples described in the guide, which was successful though very data heavy.
In the afternoon I managed to approximate Ollie's ODE model of expression and repression using simpler ODEs. I then altered my stochastic code of production and degradation of bacteria, so that production was turned off after 50s (simulating repression). I did 4 simulations, the black line shows the average of 10 realisations whilst the green is the deterministic response
Oliver says:
Big Model Summary
Was finally able to finish the real coding of the model this morning.
The purpose of the model is to:
1. Give the biochemists an approximate target for the concentration of DcmA molecules to put in each cell.
2. Give our chemist the ability to decide what value of extra-cellular DCM concentration (inside the beads) to optimise the cumulative DCM breakdown by our colony, while taking into account by-product accumulation toxicity.
3. Provide a good approximation of how much DCM we will be able to degrade and over what time scale.
4. Calculating the change in pH of the solution so that we can predict when it will become toxic to the bacteria and to potentially allow us to be capable of designing a pH safety system that allows us to predict how much buffer to add or just to let us know what allowances to make.
We start with an approximation of bacteria population over time. To start with, I have used the E-coli growth curve from before. Obviously, this is full of errors, not least the fact that it's measured in Optical Density, not number of bacteria. However, there are various websites that offer simple conversions between Optical Density and number of E-Coli bacteria per ml. Therefore, this doesn't have to have too big errors in.
The main source of errors comes in when we have no idea about the maximum population that the bacteria are likely to reach or the time scale that they will take to reach this. Therefore, take all curves as just proof of principle at present, we'll work on other correcting other approximations as time goes on.
Strand 1 - Calculating pH change
Started this by calculating the effective doubling time of the bacteria and how this changes over time (according the bacteria growth curve). The equation for this is effectively a scaled version of the assumption that bacteria are dividing obeying a power law. This seems to hold on average.
This is then used in the calculation for the rate of change of HCl in the cell. This is a temporary expression in place for when a more accurate expression is calculated.
Once the HCl concentration has been calculated, it is straight forward to calculate the pH of the system from this.
Strand 2 - Calculating the amount of DCM that we can degrade
The amount of DCM that we can degrade can be calculated from the first order ODE that I've written out above. This is an accurate expression, however knowing all of the parameters in this expression to a suitable level of detail will be a challenge.
This model currently has lots of errors and assumptions but I will be working hard to reduce this by working closely with the rest of the team. However, once this model improves and can give fairly accurate results, it will be a very powerful tool that will allow everyone in the team to optimise what they're doing so that we can design the best kit that we can in the time available.
Week 4 Day 2
Oliver says:
Worked out a way of getting around the problems I've been having with the model. Planning on making all ODEs just a very large and complex function of time. Will explain exactly what the model does when I finish getting the equations to line up.
Spent the afternoon with Phil, Emily, Tim being taught by Lucas the basics of FCS (fluorescence correlation spectroscopy). This is a technology that is advanced and allows very detailed analysis of the fluorescence of the bacteria. Whereas most labs use technology that allows analysis on a single cell level, FCS allows analysis on a single molecule level.
Matt says:
Today i have been using stochastic simulations to model a system which can produce and degrade "molecules". I did this by editing the previous code to allow for generation as well as degradation whilst allowing the simulation run for a set amount of reactions rather than waiting for all the molecules to degrade. I will also average 10 realisations and see how close it is to the idealized exponential response.
Week 4 Day 1
Oliver says:
Skyped with Sheffield iGEM team today to discuss potential collaboration. On an engineering level, the two main areas of potential collaboration are:
-Characterising one of their parts using FCS (an advanced technology that they don't have access to).
-Using our developing knowledge of stochastic modelling to allow us to build a model of their bacteria under constitutive expression.
Also carried on with the model today, it's progressing but due to the complexity and size of it, it will just take time. Also not too sure that all of the assumptions that we've made hold true, such as some equations seem to be for the details of the average bacteria, some are for the whole population. Will work on this with Jack and the biochems.
Spent the afternoon with Antonis, he suggested using Simulink to tackle the cascading ODEs.
Matt says:
Today i spent catching up with what Leroy did last week (hes not here this week) with stochastic modelling of degradation. I went through "A PRACTICAL GUIDE TO STOCHASTIC SIMULATIONS OF REACTION-DIFFUSION PROCESSES" which was really useful and will be essential for the basis of later models, i did some of the proofs and examples to make sure i understood the content which were fine if a little bit long. Thought that we could possibly also use stochastic modelling to analyse the diffusion into bead/bacteria/microcompartment as well as obviously using it for a statistical model for the degradation of bacteria/DCM. The Stochastic model also allows the user to work out the variance as well as the mean time for degradation.
Week 3 Day 5
Oliver says:
Today I carried on working out how to tackle the model. I have the first few curves sorted out, the rest look tricky. Already identified a possible major flaw in this design, the growth curve data that I'm basing my predictions on is based on the standard method of measurement. Therefore, it only reads optical density rather than actual number of bacteria. I will need to find a relationship between these parameters.
The other problem is that the bacteria growth curves are nothing to do with how the bacteria population will actually vary in the agarose beads that we're making. Basically, we have no idea how many bacteria will be present over time. This is a big problem that we will need to work closely with the biochemists to solve it.
Matt says:
This week i have been creating a light detecting circuit. I started with a photodiode (open to room light) connected to an amplifier which would give a voltage output which was dependent on the light incident, (3V with light, 4V without light). Next i created a 3V offset voltage (linked to a voltage follower so that it was stable) and put this into a comparator with the output from the amplified photdiode. This created a signal which varied from 0 to 1V, this is better than the original signal because its zeroed. I then amplified this signal so that it varied from 0 to 10V, and used this output to light an output LED. The whole process meaning that the output LED lights up when the photodiode is incident to a certain light level (this will be GFP in the final design) .
Week 3 Day 4
Leroy says:
Today was spent adding the final touches to the hyper mutagenic PCR model which I started yesterday. The model can now convert a given code in GCAT format into a numerical vector which is possible for MatLab to work with more easily. This model will now be used to simulate what happens to the DCMA code when it is being mutated.
Oliver says:
Finished off the interpolation growth curves for Psedomonas Putida this morning. This will be useful for the biochemists because it will allow them to obtain a good estimate of the growth curve for a concentration that they haven't actually tested, thus saving them lots of time. Note that this data only holds for DCM concentrations from 0mM to 200mM.
In the growth curves below this I have fitted a curve, the red dashed line is the gradient (required value by Andy). As the gradient is the desired variable, this was the most important variable to approximate with my curve.
Week 3 Day 3
Leroy says:
The day started off with a bit of a bummer. Having spent the last night investigating the breakdown of ordinary kinetics in intracellular conditions due to macromolecular crowding, I have discovered that it is not necessary to take this into consideration due to the significant size difference between formaldehyde molecules and FDHA molecules (roughly two orders of magnitude). That's research for you!
The rest of the day was spent creating a MatLab model to simulate changes in base pairs due to PCR hypermutagenesis. The first model firstly generates a random sequence of n numbers each of which is between 1 and 4 (each number represented a particular base). It was then able to randomly replace a predefined proportion of these with another base. The second model I developed was then able to replace a predefined proportion of base pairs according to relative probabilities of each of the base pair transitions.
Oliver says:
Andy provided me with more real life data; growth curves of a different bacteria (P. Putida) in various concentrations of DCM. This raw data is shown in the first graph below.
These results were closer to what was expected (reduced rate of growth in higher concentrations of DCM). I again fitted a 'S' shaped curve to these graphs, this time two separate curves for high and low concentration of DCM. These are shown below. This is important because there was such a large difference in growth when in the extremes of the concentration of DCM.
In the spirit of modelling, I now intend to create a program that interpolates between these results to give the user an estimate of the growth curve of the bacteria in DCM concentrations that they haven't yet tested. This will save them a lot of time and will enable the biochemists to estimate results that they haven't done the experiment for quickly and easily.
Week 3 Day 2
Leroy says:
Spent the morning modelling the maximum potential number of FDHA and DCMA molecules that could fit into the protein prison. Because of the complexity of the geometry of these enzymes, I modelled them as ellipsoids at which point this effectively became an ellipsoid packing problem which has been documented fairly well. In the afternoon, I began constructing an ODE model using Fick's law that would help predict the steady state concentration of formaldehyde within the cell however this can only be further progressed once I have more information about the rate constants involved in the reactions- particularly the activity level of FDHA.
Oliver says:
Matched up the growth curves. This allows us to use the growth rate (the red dotted line) to find the exact values of the gradient and therefore the exact value of the maximum growth rate in the various concentrations of DCM. This is very useful for the biochemists. The graph of this is shown below.
In the afternoon I began work on building a very large and complex model that Jack conceptualized that brings in lots of different areas of the project to model how the DCM is degraded over time. The model depends on many variables and includes factors like intracellular pH change and how this will affect growth rate of the bacteria and therefore the rate of DCM degradation.
Week 3 Day 1
Leroy says:
Getting up to speed with everything that has been done in the past few weeks particularly with regards to the repressor and activator modelling. Have been put on the modelling of the pdu micro-compartments (a.k.a. protein prisons as they shall henceforth be known). Shifted focus initially from trying to predict micro-compartment geometry from ratios of protein components to modelling the number of molecules that could fit in the protein prison (PP). Enzyme dimensions obtained from Jack. They are being modelled as spheroids and I am currently investigating the packing density of spheroids according to a number of characterizing variables e.g. sphericity and aspect ratio.
Matt says:
Spent today researching suitable LEDs for absorption of light for GFP, and suitable photodiodes for picking up the emission from it. On consulting Ciaran and the plate reader, i realised that SFGFP had significantly different peaks for absorption/emission than regular GFP. We diluted "pure" GFP up to 100 000 and tested its luminosity in the plate reader, only diluting it by 10 gave off too much light for the reader to measure and up to 100 000 there was still a readable difference.
Oliver says:
Cracking on with more modelling. I've had a chat with Andy about the growth curves that he obtained from the bacteria in different concentrations of DCM and plotted them on Matlab. This will allow me to manipulate them much more easily. I have also written a script for the solving of the first order ODE that describes general bacteria growth (it's just a combination of two delayed exponentials). It describes an initial stationary phase, then a growth phase and then a stationary phase. Having plotted this on similar scales, my plan is to match the modelled curve and the real curve to allow me to calculate the constants that describe the growth of the two types of bacteria. This will allow me to predict the growth behaviour of the bacteria for future experiments with varying concentrations of DCM without actually doing the experiment in real life. INCLUDE THIS EQUATION IN FINAL WRITE UP.
Week 2 Day 5
Oliver says:
Had the meeting this morning, very helpful and I think it should ensure we stay on track for the next week or so. Spent the day working with Jack modelling the rate of degradation of DCM by the beads, dependent on the 5 different variables that we can change by changing how we make the beads. He's not completely happy with how robust the model is though so won't let me upload the graphs yet. Something for regular followers of 'Oliver says' to look forward to!
Week 2 Day 4
Matt says:
Spent this morning learning how to produce 2D/3D graphs on matlab. In the afternoon, we thought about some ideas for having a digital (and continuous) test for when the DCM had been used up to a defined level, using comparators and light dependent resistors.
Below is a basic design for a circuit which will have a glowing (Green) LED when the fluorescent bacteria reach a certain light level (level to be found later). Once the light level is found, i will record the value of the LDR's resistance at this level, i will set R1 to this value so that the comparator will switch at this point. Depending on the design for the container this could then possibly be linked to a digital dispencer of DCM/Nutrients for bacteria.
Oliver says:
The effect of changing the activation and degradation rate of the sfGFP protein on the response of the system. This is brilliant and is exactly what synthetic biology is about. These graphs will be very useful to the biochemists as they allow them to choose a degradation and activation coefficient before they begin the experiment, thus saving them lots of time and many experiments. Therefore, they will be relying completely on this modelling, especially as this competition is so short in duration.
We are aiming for a step response in the GFP glowing, this will allow a very effective reporter system for when the bacteria have run out of DCM. Therefore, based on this model, we are going to start with a high activation coefficient because this doesn't affect the speed of response but increases the amplitude of the response. Choosing the degradation coefficient is more difficult as you have to choose between a fast response and a high amplitude of response
Therefore we're going to start off with a high activation coefficient and a low degradation coefficient; if the response of this is bright enough we'll steadily increase the degradation coefficient until we get a satisfactory speed of response of the green glow turning 'off'.
Week 2 Day 3
Oliver says:
Had a long chat with Fran, George, Ciaran and Glen this morning about the surface plot, we established that if the system behaves as the model predicts it will be very beneficial. This is because it provides a sharp cut off when the amount of DCM gets low, this is exactly what is needed as we're designing an on/off biosensor.
We established that as long as the concentration of TCY stays above a certain threshold (this threshold will remain unknown until we get lab data), the response of the system isn't affected by the concentration of TCY. Therefore, in experiments and models from now on, we will be holding TCY constant while changing the concentration of DCM. In some experiments it will be a step up and a ramp down (to simulate real life as the DCM gets degraded) and in other experiments we will be using a step up and a step down in concentration of DCM to check that our biosensor is responding correctly and robustly.
I think that the model will help to cut down the number of experiments necessary by quite a lot.
I will now plot graphs of how the GFP expression will change in response to a step up and step down in DCM concentration depending on varying expression rate and degradation rate of GFP. The biochemists assure me that these two parameters are the only two that we can realistically play around with.
Also had a chat with Jack about doing surface plots that displayed the expected output of the variation in diffusivity of DCM and H2O through the polymer that he's making, depending on the thickness of the polymer and the AcCl stoichoimetry in synthesis. This polymer will coat the agarose beads that will contain the bacteria. It will be important to maintain the correct concentration of DCM inside the beads so obtaining the correct surface plot will be important.
Plated up some bacteria cultures with Phil in the evening!
Week 2 Day 2
Matt says:
I spent today reading up on lecture notes for modelling biochemical systems and catching up with Ollie's progress. Also qualitatively described the effect of GFP's ( or DCMA) degradation rate on its production over time as it uses up the DCM.
Oliver says:
Today I pretty much nailed the time varying 3D surface plot. It allows the user to see the variation in fluorescence over time when varying amounts of DCM and tetracycline are added. It has shown how important varying time will be when taking measurements of GFP to allow the characterization of this system.
Week 2 Day 1
Oliver says:
Today was spent sat at the computer writing code. Last Thursday George introduced me to a few extra levels that were involved in the real system and so would require these extra levels to be built into the model. I have been thinking about these complications over the weekend and I'm pretty sure that I was able to work out how to modify the relevant equations accordingly.
The new model that I built in the morning took into account not only the addition of Tetracycline, but also the addition of DCM to the system. This means that the model responds much more robustly and accurately to extreme circumstances, such as when either TCY or DCM is set to zero.
In the afternoon I successfully plotted the variation in the value of steady state GFP after addition of varying amounts of DCM and TCY. Next goal is to combine these to get a surface plot!
Week 1 Day 5
Jack says:
(Part D): A very productive day designing the bacterial containment system and overall chemical/mechanical logistics;
5mm diameter agarose-bacteria 'beads' will be coated with a DCM-diffusion-limiting modified cellulose-based polymer, such that the DCM influx is less than or equal to the rate of DCM breakdown. The aim is maintaining an internal capsule [DCM] within our bacterial tolerance limits, while enabling direct capsule exposure to high [DCM]. In our physical system, the manufactured beads will have a density lower than water, lying at the water-air interface of a biphasic mixture of DCM and water, giving our bacteria access to both components by exploiting the DCM-water solubility of up to 206mM (25oC).
The DCM-polymer permeability will be controlled by the stoichiometry of acylation of the cellulose substrate - hence its hydrophobicity, and coating thickness, while overall capsule density may be modified if necessary by introducing a permeable second coating of low density.
Minimal user-intervention - How the currently proposed system will work from a user perspective:
- To a PTFE container, add in order, the ratios:
W mL DCM : X mL water : Y g 'powder mix'* : Z g capsules
(volume measurements will be aided by container graduation and masses by 'scoops' etc. provided)
*containing buffer to minimize solution pH drop on HCl production, and {biochemically necessary compounds for the bacteria}. - When system response** to complete DCM degradation is seen, the solution is safe to dispose of down the sink.
**DCM detection will be directly achieved by a GFP response from our bacteria, activating a green LED on the container lid via a photodiode circuit.
The strengths of this setup are minimal user intervention and the direct, quick, and potentially low-cost measurement of [DCM] using synthetic biology. The latter could be extended as a stand-alone DCM-detection device. As HCl is more soluble in water than DCM, the greater the H2O/DCM vol. ratio, the lower the rate of aq. pH drop with HCl production. This is something we can model and optimise.
Next, for me, is to experiment producing agarose beads by various methods, do kinetic calculations, and identify coating methods that the bacteria will survive.
Oliver says:
Sheffield meet up!
Week 1 Day 4
Oliver says:
Spent the morning with Jack looking at where the parameters come in. Played with the model and after speaking with George discovered that I hadn't modelled quite what the system is.
Week 1 Day 3
Jack says:
(Part A): Modelled the thermodynamics of solution-vapour equilibration, justifying our [DCM] approximation by calculating its deviation due to this effect.
Oliver says: - Major Breakthrough
Finished the first draft of the model, will leave it until we have real data to feed back into the system. The model is very robust and allows any user to input a large variety of parameters and scenarios that could be realistically expected in the laboratory results. The output of the model is the colour that you can expect over time (the outputs of the real system will be from a combination of mCherry and GFP).
The model reveals surprising results, including how even a small basal rate of gene expression (due to leakage of the promoters) can really change the results.
The way that I finally got the model to work was by returning to the ODE15s function in Matlab and not bothering with Laplace transforms. Information on how to use Matlab to model repressor and activator networks very easily, accurately and quickly will be uploaded to this wiki soon! If you want more details please don't hesitate to contact us.
Week 1 Day 2
Oliver says:
Today was difficult. It was spent trying to write Matlab code to solve the differential equations. Having already written the code successfully for an autorepressor and an autoactivator using the built in function ode15s, I thought it would be relatively easy to use similar code to model a network. However, I ran into quite a lot of problems with transferring all of the required values back and forth between the function script and the data entry script.
In the afternoon, I tried to get the model to work using Laplace transforms and more specifically Matlab's incredible computing ability at calculating the inverse laplace transform of complex functions to allow solutions to be obtained. However, this presented more problems than the ode15s function due to vector sizes and things that quite quickly got quite messy.
Help with the autorepressor/autoactivator code will be up on the wiki shortly, please don't hesitate to contact us in the meantime for more info though.
Week 1 Day 1 - Conceptualizing part B
Jack says:
(Part B): day 1 modelling was spent setting up a kinetic 'map' of the tetR system as a biological repressor analogue to uncharacterised dcmR. Stochastic kinetic data was found 2 and required coefficients approximated (relative orders of magnitude) from these data sets will be fed into Ollie's ODE Model.
Oliver says:
The morning was spent with Glen and Fran (who are working on part B) discussing exactly what network of activation and repression we were trying to categorize and turning it from Snapgene files (that the Biochemists understand) into a series of possible repression and activation scenarios.
Then, it was a matter of condensing the network of seemingly complex interactions into a set of differential equations with the relevant constants. This allows the response of the system to an external known input be accurately modeled.
 "
"