Team:BGU Israel/Modeling/Aspiration Shift

Our objective in ‘Aspiration Shift’ was to create a self-regulated mechanism leading to a limited expression of PGC-1a. To ensure this important feature, we designed a mathematical model that describes this mechanism. We wanted to explore the effects of the treatment, which are the introduction of two plasmids, on PGC-1a levels.

Lower and upper bound of the treatment effects:
Lower Bound
The model is based on the fact that the internal production of PGC-1a in a person cannot change by the treatment. In other words, we wanted our treatment to only make an improvement in the PGC-1a production and the production rate will not decrease below the natural rate.
Upper Bound

The main goal of our model is to verify that the effect of the treatment will not be the same for lean person and for obese person. In lean healthy people, the mean PGC-1α is higher than in obese people [1]. So regardless to the different starting points, the increment of PGC-1α due to our treatment will not reach to a dangerous level, no matter whether it is lean or obese person.

Figure 1 –Comparison between relative changes in PGC-1α overexpression (%)
 and changes in insulin-stimulated glucose utilization (%)

We know that an excessive increment in PGC-1α could harm the glucose utilization [2]. We set this threshold of increment to 80%. An increment to any person that will make it over 80%, will not be beneficial, and will even decrease the glucose utilization.

Methods & Tools
While working on the model we used MATLAB SimBiology for the design of the model diagram and for running simulations on various parameters and variables. The solving of the differential equation system were conducted using Simbiology, as well as the creation of most of the plots that we show here. Another powerful tool we used for analyzing our model was Wolfram Mathematica. We used Mathematica for investigating the characteristics of the equations in a more analytical way.

The Model Design
We conducted the design of our model of the dynamic system using MATLAB SimBiology. We defined all the variables and the dynamic interactions, which are relevant to the genetic circuit. The behavior of the circuit depends on a group of differential equations that we constructed from the diagram, which describe chemical reactions and the change of the dynamic variables with time.

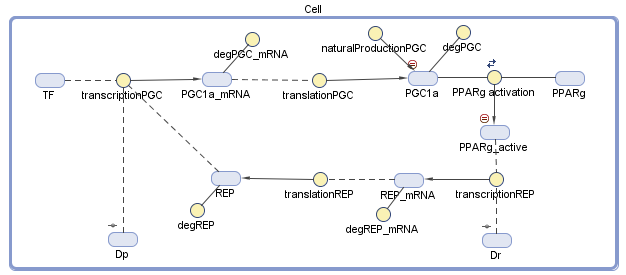
Figure 2 –The diagram of the model: The blue objects represent the variables and the yellow circles represent the interrelationship between the variables. The treatment comes in the form of the two plasmids, Dp and Dr, that we secrete into the body

A reaction of translation, for example, assumed to have a Michaelis-Menten behavior, when only the DNA transcription factor complex is able to make mRNA. On equation 1.1, the first part demonstrates the synthesis of the PGC-1α mRNA while the repressor acts as an inhibitor.

The system of the differential equations

Because the repressor and the transcription factor bind to different sites on the plasmid, the inhibition is assumed to be noncompetitive. The 1.2 equation describes the synthesis of PGC-1α in translation from its mRNA, and its natural synthesis in the cell. Equation 2.3 describes equilibrium between PPARγ and its PGC-1α Ligand. The RXR and other factors, which have an influence on the active complex, were neglected because we assumed they can join into the constant value, so the PPARγactive element is acting as an active transcription factor. Although degradation of mRNA and translation of a protein are dependent on the amount of base pairs, we assumed the same values of the PGC-1α gene to the repressor gene.

The initial values of the system variables

Figure 3

(*) will not change during treatment

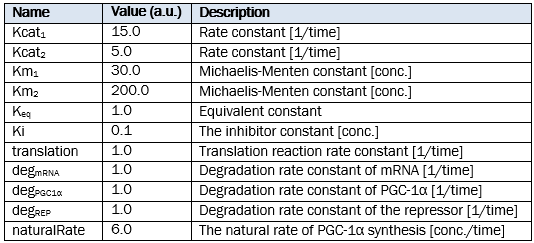
Parameters of reactions

Figure 4

Doses of the treatment

Figure 5

General behavior

In order to simulate the effects of our treatment, we added the two plasmids, DP and DR, and created a plot of the concentration levels of all the relevant variables.

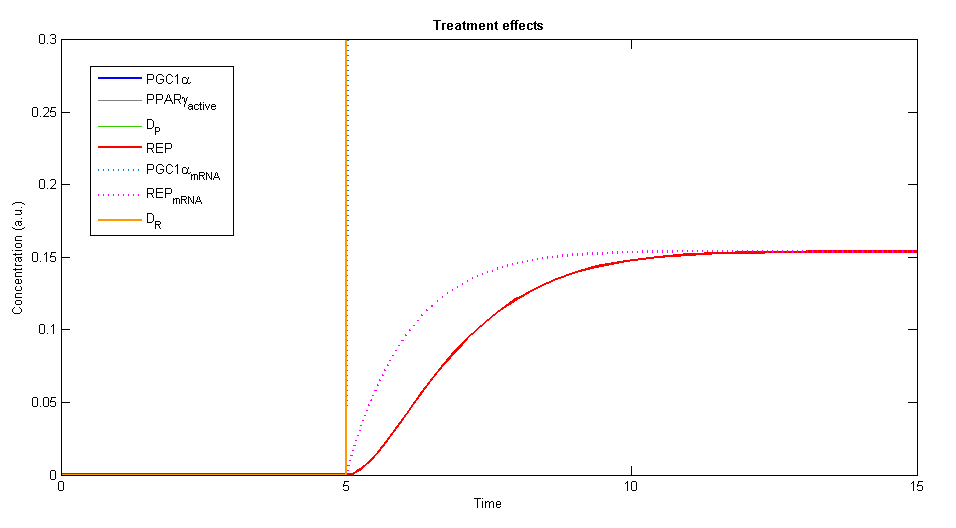
Figure 6,7- The general description of the influence of the two plasmids on the system, while the two plasmids (DP and DR) are added at time=5. The elements of PGC-1α, the active PPARγ and the repressor are rising until a specific value and stay constant at steady state

Using Wolfram Mathematica we studied the behavior of the dynamic system. The system showed similar behavior in various ranges of parameters values. A steady state is always achieved, stabilizes the levels of the variables in the system into values that depend in the given parameters.

Figure 8- Parameters manipulation in Wolfram Mathematica

Another method for investigation the steady state behavior is the eigenvalues of the corresponding Jacobian matrix of the dynamic system. By defining our system variable as the vector (PGC1αmRNA, PGC1α, REPmRNA, REP), the Jacobian matrix is:

Figure 8

In every set of parameters chosen, we could calculate the eigenvalues of J and found the behavior of the system at steady state:

• All the eigenvalues have negative real parts: Stationary point (stable)
• One of the eigenvalues has a positive real part: Stationary point (unstable)
• If the largest real part of the eigenvalues is zero: No stable point

Assignment of the parameters values we showed above shows that the system will be in a stable stationary point after the introduction of the treatment.

Regulated vs. Unregulated treatment
The modest expression mechanism has to meet two challenges. First to prevent too much synthesis of PGC-1α, that would make an increment over 80% in its concentration. The second challenge is the need to be very potent in cells with low PGC-1α activity, but to have minimum effect in cells with regular PGC-1α activity. The synthesis of the repressor supposes to meet the first challenge. As we can see in Figure 9, an unregulated mechanism without a repressor would lead to much more production of PGC-1α and could cross to a risk increment. To prove our mechanism produce around 80% of production we should test it in the lab, the model here just illustrate the potential.

Figure 9-The threshold located at 80% increment of PGC-1α. The PGC-1α level does not pass the threshold as a result of the regulated treatment, unlike the unregulated treatment

The input level of PGC-1α, in a steady state before the introduction of the plasmids, can be simply determined like this:

To face the second challenge we examined different values of natural rate of production of PGC-1α. We ran the model with different input rates and measured the increment in PGC-1α from its initial value to its final value on steady state (Figure 10).

Figure 10-For different initial levels of PGC-1α, the treatment increased it in different relative amounts

PGC-1α level stabilizes at the steady state of the system. If we give our regulated treatment to people with different natural production rate of PGC-1α from each other, the system stabilizes on different increment. This important feature provides the personalized medicine properties to our regulated treatment we designed.

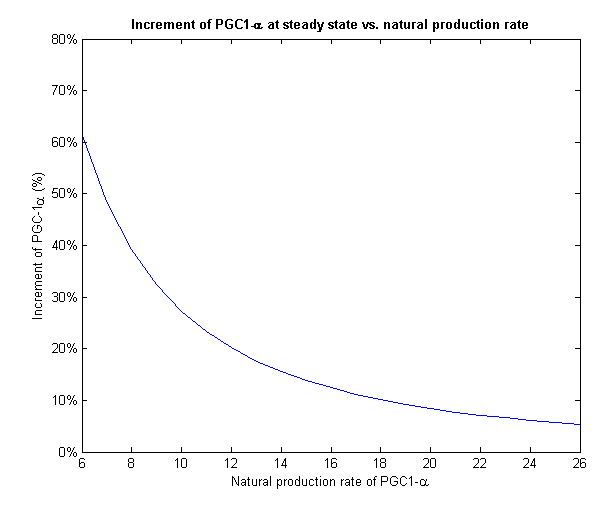
Figure 11-The increment of PGC-1α decreases with the growth of the natural production rate

At low input of PGC-1α we can see a much more drastic raise in its concentration and a fixation on higher increment than high input values. On Figure 11 we can only see the final increment on the steady state. We clearly see a decline which shows that in cells with natural high levels of PGC-1α the influence of the plasmids will be insignificant.

Conclusion:

The model shows that our treatment is personalized and self-regulated. In other words, for those who have inefficient internal production rate, the increment of PGC-1α, as a result of our treatment, will be the more significant than healthy and lean people. This concludes and confirms our method of design in order to achieve the main goal for this treatment.