Team:Valencia UPV/Modeling/fba
From 2014.igem.org

Modeling Pheromone Production Overview
Pheromones production rates can be estimated using constrained-based modelling of metabolic networks.This can be useful to know about the amount of pheromone that can be produced by the synthetic plant.
Constraint-based modelling
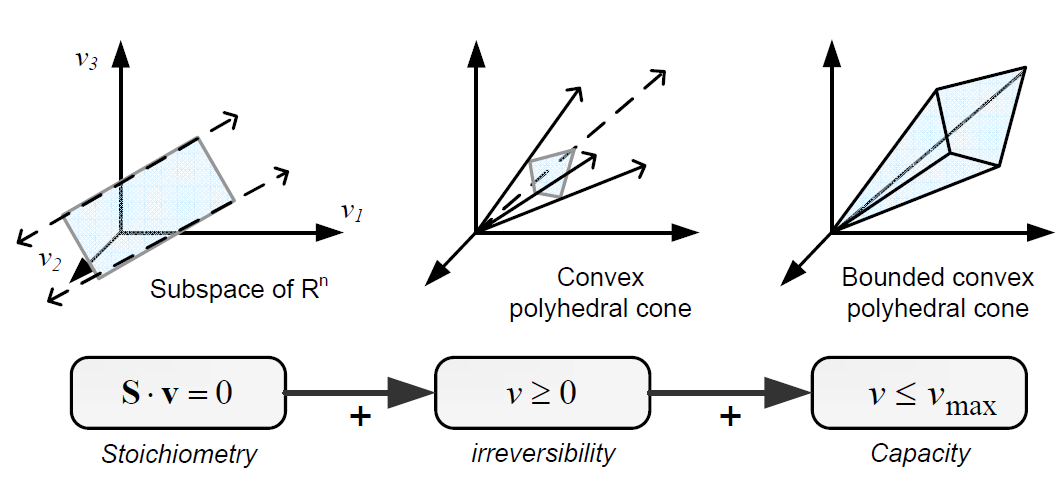
Constraint-based modelling is based on the fact that cells are subject to constraints that limit their behaviour (Palsson, 2006). In principle, if all constraints operating under a given set of circumstances were known, the actual state of a metabolic network could be elucidated. So by imposing the known constraints, it is possible to determine which functional states can and cannot be achieved by a cell. [[Stoich_model.png|600px|center|Principles of the stoichiometric modeling framework. Given a metabolic network, the mass balance around each intracellular metabolite can be mathematically represented with an ordinary differential equation. If we do not consider intracellular dynamics, the mass balances can be described by a homogeneous system of linear equations: the so-called general equation. Other constraints can be also incorporated to further restrict the space of feasible flux states of cells. Taken from: PhD Thesis. F Llaneras. UPV. 2010]]
Types of contraints
Constraints can be divided in two main types: non adjustable (invariant) and adjustable ones. The former are time-invariant restrictions of possible cell behaviour, whereas the latter depend on environmental conditions, may change through evolution, and may vary from one individual cell to another. Examples of non adjustable constraints are those imposed by thermodynamics (e.g, irreversibility of fluxes) and enzyme or transport capacities (e.g, maximum flux values). Enzyme kinetics, regulation, and experimental measurements are examples of adjustable constraints. To study the invariant properties of a network, only invariant constraints can be used, because they are those that are always satisfied (i.e, they limit the cell capabilities). If adjustable constraints are used, the elucidated cell states will be only valid under the particular set of circumstances in which these constraints operate.
Flux Balance Analysis
Flux balance analysis (FBA) is a mathematical approach for analyzing the flow of metabolites through a metabolic network. FBA is a widely used for studying biochemical networks, in particular the genome-scale metabolic network reconstructions that have been built in the past decade. These reconstructions contain all of the known metabolic reactions in an organism or plant, and the genes that encode each enzyme. In our case, FBA will calculate the flow of metabolites through our metabolic network to obtain the major production of pheromone.
COBRA
The COnstraints Based Reconstruction and Analysis (COBRA) approach to systems biology accepts the fact that we do not possess sufficiently detailed parameter data to precisely model, in the biophysical sense, an organism or plant at the genome scale [1]. The COBRA Toolbox [2] is a freely available Matlab toolbox can be used to perform a variety of COBRA methods, including many FBA-based methods. Models for the COBRA Toolbox are saved in the Systems Biology Markup Language (SBML).
References
[Llaneras08] Llaneras F, Picó J (2008). Stoichiometric Modelling of Cell Metabolism. Journal of Bioscience and Bioengineering, 105:1.
NetLogo is an agent-based programming language and integrated modeling environment. NetLogo is free and open source software, under a GPL license.
NetLogo is an agent-based programming language and integrated modeling environment. NetLogo is free and open source software, under a GPL license.
Tab #4 content goes here!
Donec pulvinar neque sed semper lacinia. Curabitur lacinia ullamcorper nibh; quis imperdiet velit eleifend ac. Donec blandit mauris eget aliquet lacinia! Donec pulvinar massa interdum risus ornare mollis. In hac habitasse platea dictumst. Ut euismod tempus hendrerit. Morbi ut adipiscing nisi. Etiam rutrum sodales gravida! Aliquam tellus orci, iaculis vel.
 "
"