Team:ETH Zurich/project/background/modeling
From 2014.igem.org
m (→Cellular Automata) |
(→Cellular Automata) |
||
| Line 2: | Line 2: | ||
==='''Cellular Automata''' === | ==='''Cellular Automata''' === | ||
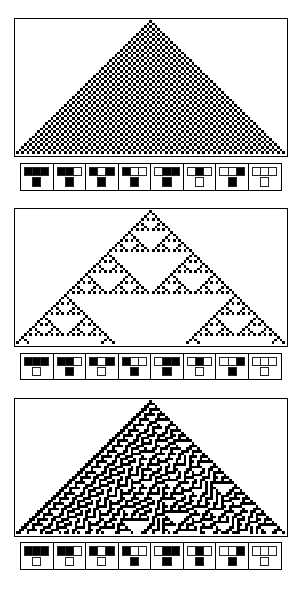
| - | Pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a cell is determined by the states of three parent cells (from the previous computation round). Those logic rules are discrete computations: they can be either implementing an AND | + | Pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a cell is determined by the states of three parent cells (from the previous computation round). Those logic rules are discrete computations: they can be either implementing an AND logic gate or another rule. Wolfram <sup>[[Team:ETH_Zurich/project/references#refWolfram|[11]]]</sup> elaborated a whole theory on these cellular automata. |
[[File:ETHZurich_CAWolfram.jpg|300px|center|thumb|Here are three different cellular automata with their logic rule.]] | [[File:ETHZurich_CAWolfram.jpg|300px|center|thumb|Here are three different cellular automata with their logic rule.]] | ||
Revision as of 19:18, 17 October 2014
Pattern Formation
Cellular Automata
Pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a cell is determined by the states of three parent cells (from the previous computation round). Those logic rules are discrete computations: they can be either implementing an AND logic gate or another rule. Wolfram [11] elaborated a whole theory on these cellular automata.
According to cellular automata theory, emergent patterns offer a large panel of properties: striking examples are the rule 30 which gives an apparently random pattern and the rule 110 which has been proven to be Turing complete. With cellular automata, you cannot predict how the final pattern will look like even if you know the rule that governs its property. Thus, the intricated computations of steps poses the problem of complexity.
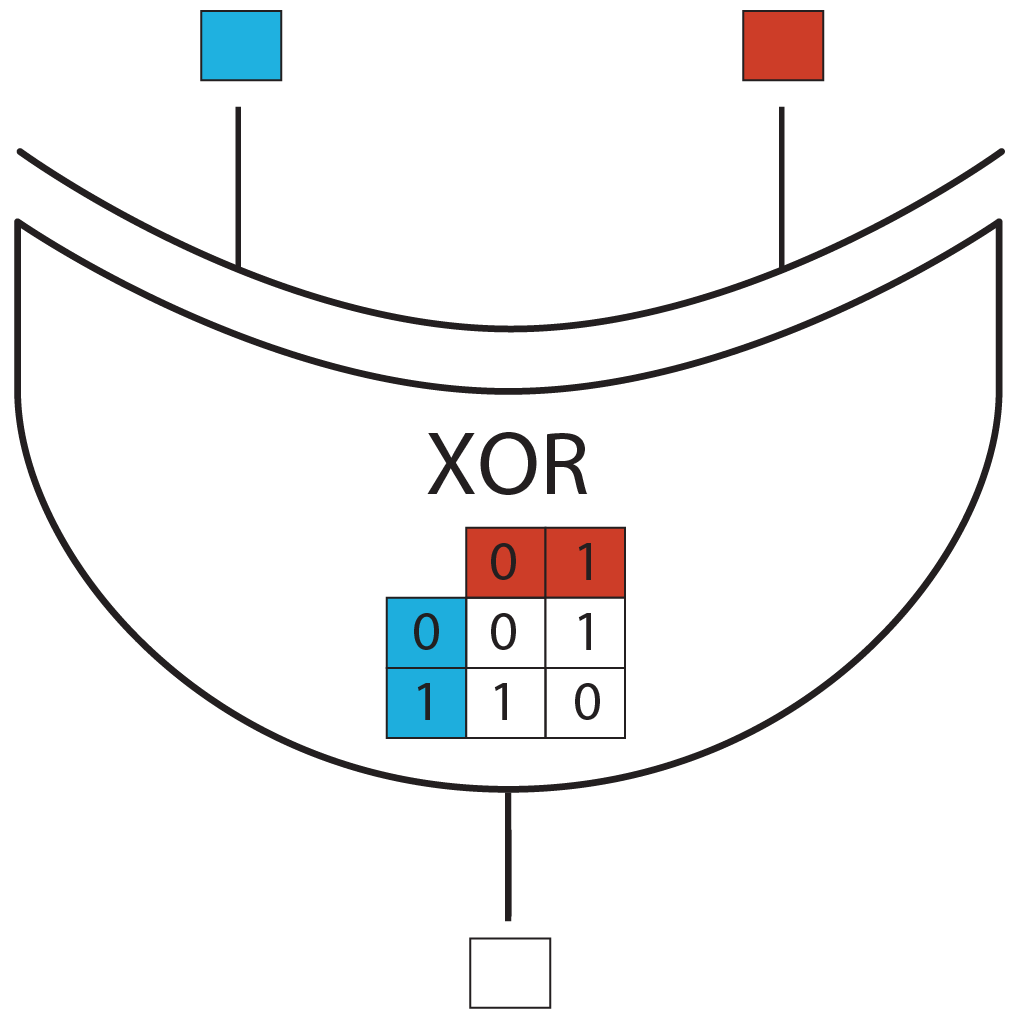
We chose to implement the XOR gate with two inputs, corresponding to rule 6. It can be considered as a first step towards the rule 110, which is an XOR with 3 inputs and is known to be Turing complete.
 "
"