Team:ETH Zurich/project/background
From 2014.igem.org
| Line 7: | Line 7: | ||
[[File:ETHZurich_TextileCone.jpg|500px|center|]] | [[File:ETHZurich_TextileCone.jpg|500px|center|]] | ||
| - | + | === Cellular Automata === | |
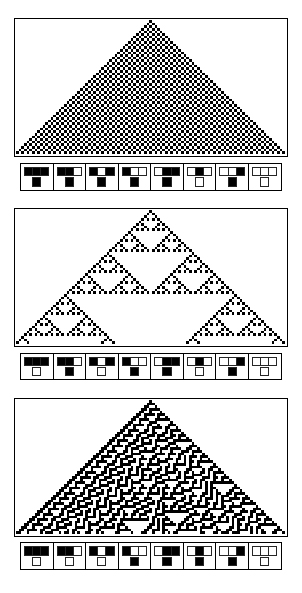
This pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a spot on the shell, corresponding to the color (either white or brown), is determined by the states of three parent spots (from the previous computation round). Wolfram <sup>[[Team:ETH_Zurich/project/references#refWolfram|[11]]]</sup> elaborated a whole theory on these cellular automata. | This pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a spot on the shell, corresponding to the color (either white or brown), is determined by the states of three parent spots (from the previous computation round). Wolfram <sup>[[Team:ETH_Zurich/project/references#refWolfram|[11]]]</sup> elaborated a whole theory on these cellular automata. | ||
| Line 13: | Line 13: | ||
According to cellular automata theory, emergent patterns offer a large panel of properties: striking examples are the rule 30 which gives an apparently random pattern and the rule 110 which has been proven to be Turing complete. With cellular automata, you cannot predict how the final pattern will look like even if you know the rule that governs its property. Thus the intricated computations of steps poses the problem of complexity. | According to cellular automata theory, emergent patterns offer a large panel of properties: striking examples are the rule 30 which gives an apparently random pattern and the rule 110 which has been proven to be Turing complete. With cellular automata, you cannot predict how the final pattern will look like even if you know the rule that governs its property. Thus the intricated computations of steps poses the problem of complexity. | ||
| + | |||
| + | |||
| + | === XOR Logic Gate === | ||
| + | |||
{{:Team:ETH Zurich/tpl/foot}} | {{:Team:ETH Zurich/tpl/foot}} | ||
Revision as of 14:15, 12 September 2014
Background
"The whole is more than the sum of its parts" Aristotle
Emergence describes how novel properties can arise from lower-complexity parts, where these properties are not observed.[12] This phenomenon is wide-spread in nature. One straight-forward example is water: from the molecules of H2O, which are here considered as simple subparts, we are able to consider the liquid "water" at a higher level of complexity, with properties such as viscosity, pressure, transparency...
One particular pattern formation retained our attention: some sea snail present a complex pattern on their shells. The "Cloth of Gold" observed on textile cones results from an inner computation of the neural cells of the sea snail. This pattern appears row by row (computation after computation) and the pigments of the next row are determined by the pigments of the row before.
Cellular Automata
This pattern formation was formalized by Neuman in the concept of cellular automata. Following a simple pre-programmed logic rule, the state of a spot on the shell, corresponding to the color (either white or brown), is determined by the states of three parent spots (from the previous computation round). Wolfram [11] elaborated a whole theory on these cellular automata.
According to cellular automata theory, emergent patterns offer a large panel of properties: striking examples are the rule 30 which gives an apparently random pattern and the rule 110 which has been proven to be Turing complete. With cellular automata, you cannot predict how the final pattern will look like even if you know the rule that governs its property. Thus the intricated computations of steps poses the problem of complexity.
XOR Logic Gate
 "
"